Download ProbabilityAndScreenSystems

Motivation:
In electromagnetic systems, the energy per photon = hn.
In communication systems, noise can be either quantum or
additive from the measurement system ( receiver, etc). The noise
power in a communication system is 4kTB, where k is the
Boltzman constant,T is the absolute temperature, and B is the
bandwidth of the system. When making a measurement (e.g.
measuring voltage in a receiver) , noise energy per unit time 1/B
can be written as 4kT.
SNR 
Nhv

N hv  AdditiveNoise
Nhv
N hv  4kT
The N in the denominator comes from the standard deviation of
the number of photons per time element.
Motivation:
SNR 
Nhv

N hv  AdditiveNoise
When the frequency n<< GHz,
Nhv
N hv  4kT
4kT >> hn
In the X-ray region where frequencies are on the order of 1019, hv
>> 4kT
So X-ray is quantum limited due to the discrete number of photons
per pixel. We need to know the mean and variance of the random
process that generate x-ray photons, absorb them, and record them.
Recall: h = 6.63x10-34 Js
k = 1.38x10-23 J/K
Motivation:
Object we are trying to detect
Contrast = ∆I / I
∆I
I
SNR = ∆I / I = CI / I
Background
We will be working towards describing the SNR of medical systems
with the model above. We will consider our ability to detect some
object ( here shown in blue)that has a different property, in this
case attenuation, from the background ( shown here in green). To do so,
we have to be able to describe the random processes that will
cause the x-ray intensity to vary across the background.
The value of a rolled die is a random process.
The outcome of rolling the die is a random variable of discrete
values. Let’s call the random variable X. We write then that
the probability of X being value n is px(n) = 1/6
1/6
1
2
3
4
5
6
Note: Because the probability of all events is equal,
we refer to this event as having a uniform probability
distribution
Probability Density Function (pdf)
1/6
p X (n)
1
2
3
4
5
6
Cumulative Probability
Distribution
1
DiscreteSy stem
F ( m)  ( p X ( n)  m)
nm
  p X ( n)
1
2
3
4
5
6
n 1
Continuous Random Variables
pdf is derivative of cumulative density function
p X ( x)  dFX ( x) / dx
FX ( x)   p X ( x)dx
x2
p[x1≤ X ≤ x2] = F(x2) - F(x1) =
0  FX ( x)  1
1. cdf is integral of pdf
2. cdf must be between 0 and 1
3. px(x) > 0
p
x1
X
( x )dx
Zeroth Order Statistics
• Not concerned with relationship between events
along a random process
• Just looks at one point in time or space
• Mean of X, mX, or Expected Value of X, E[X]
– Measures first moment of pX(x)

m X   xpX ( x)dx
• Variance of X, 2X , or E[(X-m)2 ]

– Measure second moment of pX(x)

   ( x  m )2 p X ( x )dx
2
X

 X  std
Standard deviation
Zeroth Order Statistics

• Recall E[X]   xp ( x)dx
• Variance of X or E[(X-m)2 ]
X


 X2   ( x  m ) 2 p X ( x)dx



   x p X ( x)dx  2m  x p X ( x)dx  m
2
X
2


 X2  E[ X 2 ]  2mE[ X ]  m 2
 X2  E[ X 2 ]  E 2 [ X ]  E[ X 2 ]  m 2

2
p

X
( x)dx
p(n) for throwing 2 die
6/36
5/36
4/36
3/36
2/36
1/36
2
3
4
5
6
7 8
9 10 11 12
Fair die
Each die is independent
Let die 1 experiment result be x and called Random Variable X
Let die 2 experiment result be y and called Random Variable Y
With independence,
pXY(x,y) = pX(x) pY (y)
and
E [xy] = ∫ ∫ xy pXY(x,y) dx dy
= ∫ x pX(x) dx ∫ y pY(y) dy
= E[X] E[Y] if x,y independent
1. E [X+Y] = E[X] + E[Y] Always
2. E[aX] = aE[X] Always
3. 2x = E[X2] – E2[X] Always
4. 2(aX)
= a2  2 x
Always
5. E[X + c] = E[X] + c
6. Var(X + Y) = Var(X) + Var(Y) only if the X and Y
are statistically independent.
_
If experiment has only 2 possible outcomes for each trial,
we call it a Bernouli random variable.
Success: Probability of one is p
Failure: Probability of the other is 1 - p
For n trials,
P[X = i] is the probability of i successes in the n trials
X is said to be a binomial variable with parameters (n,p)
n!
p[ X  i] 
p i (1  p) n i
(n  i)!i!
Roll a die 10 times.
In this game, you win if you roll a 6.
Anything else - you lose
What is P[X = 2], the probability you win twice?
Roll a die 10 times.
6 you win
Anything else - you lose
P[X = 2] i.e. you win twice
= (10! / 8! 2!) (1/6)2 (5/6)8
= (90 / 2) (1/36) (5/6)8 = 0.2907
If p is small and n large so that np is moderate, then an approximate
(very good) probability is:
p[X=i] is the probability exactly i events happen
P[X=i] = e - i / i!
Where np = 
With Poisson random variables, their mean is equal to their
variance!
E[X] = x2= 
Let the probability that a letter on a page is misprinted
is 1/1600. Let’s assume 800 characters per page. Find
the probability of 1 error on the page.
Binomial Random Variable Calculation.
P [ X = 1] = (800! / 799!) (1/1600) (1599/1600)799
Very difficult to calculate some of the above terms.
Let the probability that a letter on a page is misprinted
is 1/1600. Let’s assume 800 characters per page. Find
the probability of 1 error on the page.
P [ X = i] = e - i / i!
Here i = 1, p = 1/1600 and n =800, so =np = ½
So P[X=1] = 1/2 e –0.5 = .30
What is the probability there is
more than one error per page? Hint:
Can you determine the probability
that no errors exist on the page?
 ( x  m )2 
1
p X ( x) 
exp 

2
2

2 


m- m
m+
1) Number of Supreme Court vacancies in a year
2) Number of dog biscuits sold in a store each day
3) Number of x-rays discharged off an anode
Signal Power
Noise Power
If X represents power,
SNR = E[X]/ x2
If X represents an amplitude or a voltage, then X2 represents power.
SNR = E[X]/ x
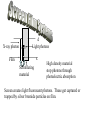
X-ray photon
d
Light photons
x
Film
Scintillating
material
High density material
stop photons through
photoelectric absorption
Screen creates light fluorescent photons. These get captured or
trapped by silver bromide particles on film.
Analysis: First calculate spray of light photons
from an event at depth x.
r

x
h (r) = h(0) cos3 
= h(0) x3 / (x2 + r2)3/2
Since cos( ) 
h(0) = K/x2
x
(x2  r 2 )
K constant
x2 inverse falloff
h (r) = Kx / (x2 + r2)3/2
H1(r) = F{h(r)}
∞
= 2π ∫ h(r) J0 (2rr) r dr where h(r) given on previous page
0
H1(r) = 2πKe - 2πxr (from a table Hankel transforms)
H(r) = H1(r) = e - 2πxr
H1(0)
( Normalize to DC Value)
H(r) = H1(r) = e - 2πxr
H1(0)
( Normalize to DC Value)
Notice this depends on x, depth of event into screen.
Let’s come up with H ( r ) based on the likelihood of
where events will occur in the scintillating material.
F(x) = 1 - e - mx for an infinite screen
Probability an x-ray photon will interact in distance x
F(x)
x
p(x) = dF(x) / dx = m e -mx
For a screen of thickness d
F(x) = 1 - e -mx / 1 - e -md
, then
me  mx
p( x ) 
since we are only concerned
1  e  md
with captured photons
H(p) = ∫ H(r,x) p(x) dx
d
= (1/ 1 - e -md )∫ e -2π x r me-mx dx
m
 d ( 2r  m )
H (r ) 
[
1

e
]
 md
(2r  m )(1  e )
Typical d = .25 mm, m=15/cm for calcium tungstate screen
m
 d ( 2r  m )
H (r ) 
[
1

e
]
 md
(2r  m )(1  e )
We would like to describe a figure of merit that would describe
a cutoff spatial frequency, akin to the bandwidth of a lowpass filter.
For a typical screen with d approximately .25 mm
and m=15/cm for a calcium tungstate screen, the bracketed term above
can be approximated as 1 for spatial frequencies near the cutoff.
Figure of Merit
k
0.1
1.0
10 Cycles/mm
rk
For moderate k, (i.e. a cutoff frequency)
H (r )  k 
m
(2rk  m )(1  e ud )
Let (1 - e -md) =  the capture efficiency of the screen
Then k ≈m / (2πpk + m)
2πk  pk = (1 - k) m
For k << 1
m
pk 
2k
: As the efficiency increases, rk decreases.
This is because  increases as d increases.
d1
d2
phosphor
phosphor
x
Double
Emulsion
film
Intuitively, we would believe this system would work better . Let’s
analyze its performance. Let d1 +d2 = d so we can compare
performance.
H(r,x) = e -2πr (d1-x)
H(r,x) = e -2πr (x –d1)
for 0 < x < d1
for d1 < x < d1 + d2
d,
d2
H(r) = (m/ 1- e -md) { ∫ e -2πr (d1 - x) e - mx dx + ∫ e -2πr (x –d1) e - mx dx}
0
d1
= (m / 1- e -md) [ ((e -md1 - e -2πr d1) / (2πr - m))
+ ((e -md1 - e -(2πr d2 + md) / (2πr + u) )]
Again lets determine a cutoff frequency of rk for a low pass filter that
has a response of H(rk) = k,
If we assume d1 ≈ d2 = d/2, than we can neglect
e -2πrd, e -2πrd1 , e -2πrd2 because they will be small even for relatively
small spatial frequencies. e –ud is also small compared to e –ud1
Since (2πr)2 >> u2
1
1
2


2r  m 2r  m 2r
m
2
H ( pk )  k  e  md1

2rk
is true for all but lowest frequency, then
m
rk 
2e  md
2k
1
rk 
m
(2e ud )
2k
1
Compare this cutoff frequency to the single screen cutoff.
Concentrate on the factor 2e-md1
( the new factor from the
single screen film)
Since
  1  e  md
e  md / 2  1  
So    2e  md / 2  2e  md1  2 1  
Improvement is
2 1 
With ≈ 0.3, improvement is 1.7
Use improvement to lower dose, quicken exam, improve contrast,
or some combination.
Assuming a circularly symmetric source,
Id (xd, yd) = Kt (xd/M, yd/M) ** (1/m2) s (rd/m) ** h (rd)
Detector response is also circularly symmetric.
Id (u,v) = KM2T (Mu,Mv) S(mp) · H(p)
H0(p)
Spatial frequencies at detector
Object is of interest though
Id (u/M,v/M) = KM2T (u,v) S((m/M)p) · H(p/M)
Product of 2 Low Pass Filters.
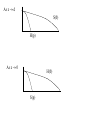
H0(p) = S [(1-z/d) p ] H ((z/d)p)
As z  d
S(0)
H(p)
As z  0
H(0)
S(p)