Download Section 6.1 and 6.2 Probability

Section 6.1 and 6.2
Probability
Probability; it’s all chance!


The big idea in probability is that chance
behavior is unpredictable in the short
run but follows a regular, predictable
pattern in the long run.
Probability is a mathematical model
for what SHOULD happen!!
A Common Question

The probability of tossing a coin and it landing
on Heads is 0.5. Theoretically, then, if I toss the
coin 10 times, I should get 5 Heads. However,
with such a small number of tosses there is a lot
of room for variability.

There are two games involving flipping a coin.



Game 1: You win $2 if you throw 40% - 60% heads.
Game 2: You win $10 if you throw more than 75% heads.
For which game would you rather toss the coin 5
times? 500 times?
The Idea of Probability




Random does NOT mean haphazard. Random
events have an order that emerges in the long
run.
Random – individual outcomes are uncertain,
but there is a regular distribution of outcomes in
a large number of repetitions.
Probability – proportion of times the outcomes
would occur in a very long series of repetitions.
Independent – the outcome of one trial does not
influence the outcomes of any other trial (ex.
Rolling a die).
Properties



Remember that probabilities are like
proportions; therefore, probabilities will
always be a number between 0 and 1
(inclusive).
The probability that I draw a 15 from a
standard deck of cards is 0.
The probability that I draw a red or a
black card from a standard deck is 1.
Probability Models



Sample space S is the set of all the possible outcomes.
 If I toss 2 coins, and count the number of heads, the
sample space is {0, 1, 2}.
An event is any outcome or set of outcomes of a random
phenomenon.
 An event for tossing 2 coins might be getting at least
1 head.
A probability model is a mathematical description – it
lists the sample space and the probabilities associated
with each event.
Word of the Day:
Enumeration

It will be critical for you to be able to list
(enumerate) all the possible outcomes of
a random phenomenon.

Examples: List all the possible outcomes.
How many are there? Then write the sample
space.
Roll 2 dice
 Roll 1 die and toss a coin

Two techniques can help us with
enumeration…

Tree Diagrams



Draw the “branches” for the first task, and then from
each of those branches, draw the branches for the
second task.
Let’s do this to represent the sample space for
throwing one die and flipping a coin.
Multiplication Principle

Multiply the number of outcomes for the first task by
the number of outcomes for the second task. Do this
for rolling two dice.
Example


List the sample space for how many boys
you could have within three children.
Give the probability model for this
situation.
Probability Rules




Any probability is a number between (and
including) 0 and 1.
All possible outcomes together must have
probability = 1.
The probability that an event does NOT occur is
one minus the probability that the event does
occur.
If two events have no outcomes in common,
then probability that one OR the other occurs is
the sum of their individual probabilities.
Any probability is a number
between (and including) 0 and 1.

In symbols:
0 ≤ P(A) ≤ 1


Probabilities can not be negative!
Probabilities can not be greater than 1!
All possible outcomes together
must have probability = 1.

In symbols.. The probability of the whole sample space:
P(S) = 1

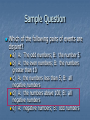
Sample question: A randomly selected student is asked to respond
yes, no, or maybe to the following question, “Do you intend to vote
in the next presidential election?” The sample space is {yes, no,
maybe}. Which of the following represents a legitimate assignment
of probabilities for this sample space?





A)
B)
C)
D)
E)
.4, .4, .2
.4, .6, .4
.3, .3, .3
.5, .3, -.2
None of the above
The probability that an event does
NOT occur, called the complement( AC )
is one minus the probability that the
event does occur.

In symbols:
P( A )  1  P( A)
C

Sample question: If you choose a card at
random from a well-shuffled deck of 52
cards, what is the probability that the card is
not a heart? P(Heart) = 13/52 = ¼
P(Not a Heart) = 1 – P(Heart) = 1 – ¼ = ¾
If two events have no outcomes in common,
then probability that one OR the other occurs
is the sum of their individual probabilities.


Having no outcomes in common is called
DISJOINT or MUTUALLY EXCLUSIVE.
This rule is very important!

It’s called the addition rule for disjoint events.
In symbols:
P(A or B) = P(A U B) = P(A) + P(B)

This is read
“A union B.”
Sample Question

Which of the following pairs of events are
disjoint?





a) A: The odd numbers; B: the number 5
b) A: the even numbers; B: the numbers
greater than 10
c) A: the numbers less than 5; B: all
negative numbers
d) A: the numbers above 100; B: all
negative numbers
e) A: negative numbers; B: odd numbers
More Symbols




{A ∩ B} “A intersect B” – this means the
outcomes that A and B have in common
If A ∩ B = Ø, then A and B are disjoint!
WHY?
C
1
What is A U A ?
What is A ∩ AC? Ø
Another thing to remember

The probability that something will occur
AT LEAST ONCE
1 – P(event does not happen)how many attempts
Example: If the probability that I pass any
given Statistics test is 70% and I have 10
tests this semester, what is the probability
that I pass at LEAST ONE?!
Homework
6.4, 6.9, 6.11, 6.14, 6.18, 6.34,
6.36