* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Prior Elicitation from Expert Opinion
Survey
Document related concepts
Transcript
Prior Elicitation from Expert
Opinion
Dipak K. Dey
University of Connecticut
Some parts joint with:
Junfeng Liu
Case Western Reserve University
1
Elicitation
Elicitation is the process of extracting
expert knowledge about some unknown quantity
of interest, or the probability of some future event,
which can then be used to supplement any
numerical data that we may have.
If the expert in question does not have a statistical
background, as is often the case, translating their
beliefs into a statistical
form suitable for use in our analyses can be a
challenging task.
2
Introduction
Prior elicitation is an important and yet under
researched component of Bayesian statistics.
In any statistical analysis there will typically be some
form of background knowledge available in addition
to the data at hand.
For example, suppose we are investigating the
average lifetime of a component. We can do tests
on a sample of components to learn about their
average lifetime, but the designer/ engineer of the
component may have their own expectations about
its performance.
3
Introduction
If we can represent the expert's uncertainty
about the lifetime through a probability
distribution, then this additional (prior)
knowledge can be utilized within the Bayesian
framework.
With a large quantity of data, prior knowledge
tends to have less of an effect on final
inferences. Given this fact, and the various
techniques available for representing prior
ignorance, practitioners of Bayesian statistics
are frequently spared the effort of thinking about
the available prior knowledge.
4
Introduction
It will not always be the case that we will have
sufficient data to be able to ignore prior knowledge,
and one example of this would be in the uncertainty
in computer models application or modeling extreme
events.
Uncertain model input parameters are often
assigned probability distributions entirely on the
basis of expert judgments. In addition, certain
parameters in statistical models can be hard to
make inferences about, even with a reasonable
amount of data.
5
Introduction
The amount of research in eliciting prior
knowledge is relatively low, and various
proposed techniques are often targeted at
specific applications. At the same time, recent
advances in Bayesian computation have allowed
far greater flexibility in modeling prior
knowledge. In general, elicitation can be made
difficult by the fact that we cannot expect the
expert to provide probability distributions for
quantities of interest directly.
6
Introduction
The challenge is then to find appropriate
questions to ask the expert in order to
extract their knowledge, and then to
determine a suitable probabilistic
description of the variables we are
interested in based on the information we
have learned from them.
7
Motivation
Three approaches:
[1] Direct Prior Elicitation:
Berger (1985) Relative frequency, and quantile based elicitation.
[2] Predictive prior probability space, which requires simple
priors and may be burdened with additional uncertainties
arising from the response model.
(Kadane, et al, 1980; Garthwaite and Dickey, 1988, Al-Awadhi and Garthwaite, 1998,
etc.).
[3] Nonparametric Elicitation:
(Oakley and O’Hagan, 2002)
8
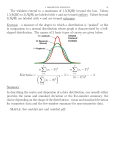
Symmetric Prior Elicitation
Double bisection method: Expert provides
q(.25), q(.5) and q(.75), the three quantiles
IQR = q(.75)-q(.25)
Normal prior:
Z(q)= IQR of std. normal, then, prior mean
and std. dev. are,
q(.5) and IQR/ Z(q) respectively.
9
Student’s t Prior
Three non redundant quantiles are required
to estimate the df ν. Kadane et.al. (1980)
suggested obtaining q(.5), q(.75) and
q(.9375)
a(x) = (q(.9375)-q(.5))/(q(.75)-q(.5)) depends
on df ν only
Df is determined from look up table of a(x) vs
df ν.
10
Student’s t Prior
After elicitation of df obtain tν,0.75
Calculate S(q) = (q(.75)-q(.5)) 2/ t2ν,0.75
for elicitation of scale parameter σ.
This idea can be applied to any general
location-scale family.
11
Lognormal Prior
Garthwaite (1989) used split-normal distribution,
O’Hagan (1998) used 1/6, 3/6 and 5/6 quantiles.
Proposition: If X has a log-normal distribution, i.e.,
2
2
2
ln X ~ N ( , 2 ) , then the variance D( X ) q0.50r (r 1)
and the mean E ( X ) rq0.50 ,where q0.50 e is the
2
ln
median of X , r exp( (q.75 / q.25 ) 2 ), Z q is the IQR
2Z q
for standard normal distribution.
12
Direct Prior Elicitation
(1) Simple and limited prior family with only location
and scale parameters (normal, exponential, etc.)
(2) Location-scale-shape (µ--) parameter joint
elicitation (gamma, skew-normal, Student’s t, etc.)
13
Symmetric and Asymmetric Priors
•
Normal
•
Student’s t
x 2
1
exp
2 2
2
v 1 /2
v v /2
1 x
2
/v
Location-scale, symmetric
v 1
2
No location scale but shape,
symmetric
ln x 2
exp
2 2
x 2
1
•
Log-normal
•
Skew-normal
•
Normal-exponential
•
Skew-Student’s
Location-scale, asymmetric
2 x x
t
Location-scale-shape, asymmetric
2 x x
exp exp
2
Location-scale-shape, asymmetric
v 1
2
2
2 v 1 /2 1 x
1
v v /2
v
0.5
2
x
v
x
T1,v 1
v 1
Location-scale-shape, asymmetric
14
Shape Parameter Elicitation
This is most challenging.
Presumably, the Interquantile-Range-ratio (IQRR= [q(.75)q(.5)]/[q(.5)-q(.25)] is a monotone function of shape parameter.
We have two cases:
(1) Shape-parameter is in the non-sensitive region, absolute value
larger than 1.
(2) Shape-parameter is in the sensitive region, absolute value
smaller than 1.
15
Nonsensitive and sensitive regions (Skew-normal)
Non-sensitive
Sensitive
IQRR (interquantile range ratio) vs. shape parameter
16
Shape Parameter Sensitive Region: Gamma
Case
17
Parameter Elicitation Guideline:
The elicitation input is IQRR and the hyperparameter
is the shape parameter.
We prefer a moderate sensitivity index (SI):
Hyperparameter change / elicitation input change
SI=∂ (IQRR)/∂ (l)
We look for SI close to 1.
Sensitive region: shape parameter is small in
magnitude.
18
Parameter Elicitation on Shape Parameter NonSensitive Region
(1) Elicit shape parameter from plot of
IQRR() vs.
(2) Scale parameter
= IQR/IQR()
where, IQR is the interquantile range from expert, IQR() is the standardized
IQR with elicited from (1), =1 and µ=0.
(3) The location parameter is
Q(0.75)- Q(0.75,)
where, Q(0.75) is .75 quantile from expert, comes from (2), and Q(0.75,) is
the standardized .75 quantile with elicited from (1), =1 and µ=0.
19
Note:
The sensitivity index in “IQR() vs. ” and “Q(0.75,) vs. ” is usually moderate.
20
Approximate Scale Parameter Elicitation from
Taylor’s Expansion (1: Basics)
General approach for any location, scale and shape
Family:
[1] g(*) is the characteristic point of density f(x|µ,,), say mean, median,
mode, etc.
[2] g(*) = µ+g(), where g() is the standardized characteristic point.
[3] f(g(*)|µ,,) = (1/)f(g()|0,1,).
21
Approximate Scale Parameter Elicitation from
Taylor’s Expansion (2: Method)
Letting (1)-(2) and only keeping first 2 terms on the right hand side, we get
1
f ,0,1 (g())IQR
We get the approximate scale parameter without considering any
consequences as
2 IQR f ,0,1 (g())
22
Relative Error in Student’s t Prior Elicitation
(1: Values)
1
IQR
ˆ
From Taylor’s expansion, we have approximate
p
IQR
The exact
T0.75, T0.25,
Where,
2
2
[1] v is degrees of freedom
[2] IQR is interquantile range from expert
[3] p = 0.5
[4] T0.75,v is .75 quantile of Student’s t distribution with v degrees of freedom
23
Approximate Scale Parameter Elicitation from
Taylor’s Expansion (3: Relative Error)
Now
(1)-(2)
Denote
(Only related to )
The relative
error is
2
1 2
24
Relative Error in Student’s t Prior Elicitation
(2: Plot)
Zp
(1) ``approximate” represents Taylor expansion value:
ˆ
IQR
p
1
2
2
IQR
T0.75, T0.25,
(2) ``exact” represents Taylor expansion value:
(3) ``normal” represents IQR
, with Z p as interquantile range for standardized normal distribution.
Z
p
(1) : (2) approaches
1.0763 as v goes to infinity.
25
An Important Observation
When shape parameter is highly sensitive to IQRR, the approximate scale
parameter elicitation by Taylor’s expansion will be very stable in terms of
relative error.
26
Elicitation of Shape Parameter on Sensitive Region
(Skew-normal, Iteration on characteristic points)
2
Iteration based on Taylor’s expansion at median q0.50,, mode M or mean E
.
1 2
(1) Start with current l, from high-proportional- fidelity by Taylor expansion, we have
2
(q
IQR[2
Z )
p
0.50, )( q0.50, )] /(
q
(2) The skew(shape) parameter can be obtained by plotting
q0.75, q0.50, ~
(3) Go to (1) until convergence (complete
and )
(4) Location parameter
q0.25 q0.25,
27
Elicitation on Shape Parameter Sensitive Region
(Skew-normal, Iteration on IQRs)
Iteration based on IQRs
(1) Start with current
, we look up
q0.75, q0.25, ~
q0.75 q0.25 , then
q0.75, q0.25,
parameter can be obtained by plot
(2) The skew (shape)
q0.75, q0.50, ~
q0.75, q0.50,
Since
and
q0.25 q0.25,
(3) Go to (1) until
convergence (complete
(4) Location parameter
q0.75 q0.50
)
28
Graphical Comparison 1 (reference: IQR based
iteration)
29
Graphical Comparison 2 (reference: median based
iteration)
30
Graphical Comparison 3 (reference: mean based
iteration)
31
Graphical Comparison 4 (reference: mode based
iteration)
32
Another Important Observation
The IQR based iteration is close to mean based iteration for
skew-normal case, since mean is explicit E 2 1 , other
2
than numerically solved.
33
34
35
Non-Parametric Prior Elicitation
•
To estimate prior density
,
f ( ) 0
such that
f ( directly
),
f ( )d 1
Suppose, E f ( ) | g (u | ) p ,
where p = parametric family of distributions,
u
= vector of hyper parameters
= underlying parameters in p
36
Non-Parametric Prior Elicitation
Cov f ( ), f ( ) | g ( | u) g ( | u) 2c( , ),
c ( , ) =(correlation function) = 1 if
decreasing function of | | otherwise.
c ( , ) ensures that prior variance covariance matrix
of any set of observation f () or functional of
f ()
is positive semi-definite.
37
Choice of Covariance function
1
2
c( , ) exp
2b
2 : specifies the true density function.
b : controls smoothness of the density.
b large implies Corr f ( ), f ( ) is large.
(u, 2 , b)
38
Hierarchical prior
(Gaussian Process Prior)
Special Case :
g ( | u ) N (m, ) then
1
2
c( , ) exp
,
*
2b
b* b
Then (m, , 2 , b* )
Prior:
p(m, , 2 , b* ) 1 2 p(b* )
39
Let
D = elicited summaries relating to f ( ) = {data}
E ( D) H , V ( D) 2 A, Cov( D, f ( )) 2t ( )
• H is a function of m &
• A and t ( ) is a function of m, & b*
40
This implies,
f ( | D, m, , b, ) ~ MVN
2
with
E f ( ) | g ( ) t ( )T A1 ( D H ),
Cov f ( ), f ( ) | 2 g ( | u) g ( | u)c( , ) t ( )T A1t ( )
(m, , 2 , b* )
41
Posterior
p (m, , , b | D)
2
*
1
1
* 2
exp
log
b
*
b
2
1
T
1
exp
( D H ) A ( D H )
2
2
1
| A|
1
2
( n 2)
n = # of elements in D
use MCMC to obtain samples from f () | D, m, , b*
42
Other Choices of Centering
a)
g ( | ) ~ t (m, d )
b)
g ( | ) ~ SMN
c)
g ( | ) ~ Skew t (m, d , )
d)
g ( | ) ~ Gamma or Log-normal etc.
43
Side Conditions
Given Derivatives or quantiles D will be
appropriately changed. In fact D can
incorporate all the constraints specified in the
prior, e.g., moments.
44
Psychological Perspective of
Imprecise Subjective Probabilities
Numerical probabilty estimates (N)
Ranges of numerical values (R)
Verbal phrases (V)
Objective:
Translate the triplate (N,R,V) to a decision
maker’s model
45
Imprecisely Assessed
Distributions
Contamination:
g * ( | w) (1 ) g ( | w) .q( | w), q Q
g * ( | w) Class of Bi-modal distribution
P* ( A) P( A) , ~ N (0, 2 )
46
Future problems
Prior elicitation in Extreme Value Modeling
Quantile and graphical approaches for GEV
model, Coles and Powel(1996)
Prior elicitation for short and long tailed
distribution
Spatial modeling
High dimensional modeling
47
References
1. Daneshkhah, A. (2004). Psychological Aspects Influencing Elicitation of
Subjective Probability. BEEP working paper.
2. Dey, D.K. and Liu, J. (2007). A quantitative study of quantile based direct
prior elicitation from expert opinion. Bayesian Analysis, 2, 137-166.
3. Garthwaite, P. H., Kadane, J. B., and O'Hagan, A. (2005). Statistical
methods for eliciting probability distributions. Journal of the American
Statistical Association, 100, 680-701.
4. Jenkinson, D. (2005). The Elicitation of Probabilities-A Review of the
Statistical Literature. BEEP working paper.
5. Kadane, J.B.,Dickey,J.M., Winkler, R.L., Smith, W.S. and Peters,
S.C.(1980). Interactive elicitation of opinion for a normal linear model.
JASA, 75, 845-854.
48
6. Oakley, J., and O'Hagan, A. (2005). Uncertainty in prior
elicitations: a non-parametric approach. Revised version of
research report No. 521/02 Department of Probability and
Statistics, University of Sheffield.
7. O'Hagan, A. (2005). Research in elicitation. Research Report
No.557/05, Department of Probability and Statistics, University of
Sheffield. Invited article for a volume entitled Bayesian Statistics
and its Applications.
8. O' Hagan, A., Buck, C. E., Daneshkhah, A., Eiser, J. E.,
Garthwaite, P. H., Jenkinson, D. J., Oakley, J. E. and Rakow, T.
(2006). Uncertain Judgements: Eliciting Expert Probabilities. This
book Will be published by John Wiley and Sons in July 2006.
49
THANK YOU
50