* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Methods in Medical Image Analysis Statistics of Pattern
Survey
Document related concepts
Transcript
Methods in Medical Image
Analysis
Statistics of Pattern Recognition:
Classification and Clustering
Some content provided by Milos Hauskrecht,
University of Pittsburgh Computer Science
ITK Questions?
Classification
Classification
Classification
Features
• Loosely stated, a feature is a value
describing something about your data
points (e.g. for pixels: intensity, local
gradient, distance from landmark, etc)
• Multiple (n) features are put together to
form a feature vector, which defines a
data point’s location in n-dimensional
feature space
Feature Space
• Feature Space – The theoretical n-dimensional space occupied
by n input raster objects (features).
– Each feature represents one dimension, and
its values represent positions along one of the
orthogonal coordinate axes in feature space.
– The set of feature values belonging to a data
point define a vector in feature space.
Statistical Notation
• Class probability distribution:
p(x,y) = p(x | y) p(y)
x: feature vector – {x1,x2,x3…,xn}
y: class
p(x | y): probabilty of x given y
p(x,y): probability of both x and y
Example: Binary Classification
Example: Binary Classification
• Two class-conditional distributions:
p(x | y = 0)
p(x | y = 1)
• Priors:
p(y = 0) + p(y = 1) = 1
Modeling Class Densities
• In the text, they choose to concentrate on
methods that use Gaussians to model class
densities
Modeling Class Densities
Generative Approach to
Classification
1. Represent and learn the distribution:
p(x,y)
2. Use it to define probabilistic discriminant
functions
e.g.
go(x) = p(y = 0 | x)
g1(x) = p(y = 1 | x)
Generative Approach to
Classification
Typical model:
p(x,y) = p(x | y) p(y)
p(x | y) = Class-conditional distributions
(densities)
p(y) = Priors of classes (probability of class y)
We Want:
p(y | x) = Posteriors of classes
Class Modeling
• We model the class distributions as multivariate
Gaussians
x ~ N(μ0, Σ0) for y = 0
x ~ N(μ1, Σ1) for y = 1
• Priors are based on training data, or a distribution
can be chosen that is expected to fit the data well
(e.g. Bernoulli distribution for a coin flip)
Making a class decision
• We need to define discriminant functions ( gn(x) )
• We have two basic choices:
– Likelihood of data – choose the class (Gaussian) that
best explains the input data (x):
– Posterior of class – choose the class with a better
posterior probability:
Calculating Posteriors
• Use Bayes’ Rule:
• In this case,
P( A | B)
P( B | A) P( A)
P( B)
Linear Decision Boundary
• When covariances are the same
Linear Decision Boundary
Linear Decision Boundary
Quadratic Decision Boundary
• When covariances are different
Quadratic Decision Boundary
Quadratic Decision Boundary
Clustering
• Basic Clustering Problem:
– Distribute data into k different groups such that data
points similar to each other are in the same group
– Similarity between points is defined in terms of some
distance metric
• Clustering is useful for:
– Similarity/Dissimilarity analysis
• Analyze what data point in the sample are close to each
other
– Dimensionality Reduction
• High dimensional data replaced with a group (cluster) label
Clustering
Clustering
Distance Metrics
• Euclidean Distance, in some space (for our
purposes, probably a feature space)
• Must fulfill three properties:
Distance Metrics
• Common simple metrics:
– Euclidean:
– Manhattan:
• Both work for an arbitrary k-dimensional space
Clustering Algorithms
• k-Nearest Neighbor
• k-Means
• Parzen Windows
k-Nearest Neighbor
• In essence, a classifier
• Requires input parameter k
– In this algorithm, k indicates the number of
neighboring points to take into account when
classifying a data point
• Requires training data
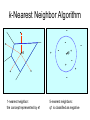
k-Nearest Neighbor Algorithm
• For each data point xn, choose its class by
finding the most prominent class among
the k nearest data points in the training set
• Use any distance measure (usually a
Euclidean distance measure)
k-Nearest Neighbor Algorithm
e1
+
-
-
q1
+
+
+
-
1-nearest neighbor:
the concept represented by e1
5-nearest neighbors:
q1 is classified as negative
k-Nearest Neighbor
• Advantages:
– Simple
– General (can work for any distance measure you
want)
• Disadvantages:
– Requires well classified training data
– Can be sensitive to k value chosen
– All attributes are used in classification, even ones that
may be irrelevant
– Inductive bias: we assume that a data point should be
classified the same as points near it
k-Means
• Suitable only when data points have
continuous values
• Groups are defined in terms of cluster
centers (means)
• Requires input parameter k
– In this algorithm, k indicates the number of
clusters to be created
• Guaranteed to converge to at least a local
optima
k-Means Algorithm
•
Algorithm:
1. Randomly initialize k mean values
2. Repeat next two steps until no change in
means:
1. Partition the data using a similarity measure
according to the current means
2. Move the means to the center of the data in the
current partition
3. Stop when no change in the means
k-Means
k-Means
• Advantages:
– Simple
– General (can work for any distance measure you want)
– Requires no training phase
• Disadvantages:
– Result is very sensitive to initial mean placement
– Can perform poorly on overlapping regions
– Doesn’t work on features with non-continuous values (can’t
compute cluster means)
– Inductive bias: we assume that a data point should be classified
the same as points near it
Parzen Windows
• Similar to k-Nearest Neighbor, but instead
of using the k closest training data points,
its uses all points within a kernel (window),
weighting their contribution to the
classification based on the kernel
• As with our classification algorithms, we
will consider a gaussian kernel as the
window
Parzen Windows
• Assume a region defined by a d-dimensional
Gaussian of scale σ
• We can define a window density function:
1
p( x , )
S
G( x S ( j ) , )
S
j 1
2
• Note that we consider all points in the training
set, but if a point is outside of the kernel, its
weight will be 0, negating its influence
Parzen Windows
Parzen Windows
• Advantages:
– More robust than k-nearest neighbor
– Excellent accuracy and consistency
• Disadvantages:
– How to choose the size of the window?
– Alone, kernel density estimation techniques
provide little insight into data or problems