* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Sensitivity and Loudness
Survey
Document related concepts
Hearing loss wikipedia , lookup
Audiology and hearing health professionals in developed and developing countries wikipedia , lookup
Olivocochlear system wikipedia , lookup
Noise-induced hearing loss wikipedia , lookup
Sound localization wikipedia , lookup
Auditory system wikipedia , lookup
Transcript
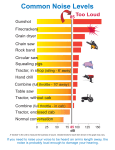
PSYC 60041 Auditory Science Auditory Sensitivity & Loudness Chris Plack Auditory Sensitivity & Loudness • Learning Outcomes – Understand how auditory sensitivity can be measured – Understand what is meant by MAF and MAP – Understand how and why threshold depends on signal duration – Understand how loudness is defined and quantified – Understand how loudness is affected by hearing loss – Understand the basic intensity sensitivity of the human ear dB SPL We generally quantify sound by measuring its pressure in Pascals (Pa = N/m2). This is converted to a logarithmic scale: dB. When the reference pressure of 20 mPa (or reference intensity of 10-12 Watts/m2) is used to calculate the level of a sound we call the measure dB sound pressure level (or dB SPL): dB SPL = 10 log10[I / (10-12 Watts/m2)] or… dB SPL = 20 log10[p / (2x10-5 Pa)] (for reference, atmospheric pressure is 105 Pa) Threshold of Audibility Threshold of Audibility A key role of the audiologist is to determine how sensitive is an ear to sounds of different frequencies. Frequency specific stimuli are used – sinusoids (“pure tones”) – one single frequency: Measuring Threshold The intensity of the sound can be adjusted to find the smallest level required for detection – threshold of audibility. However our detection of a sound isn’t as simple as just “yes I can hear it” or “no I can’t hear it.” Sounds near threshold sometimes result in yes and sometimes no for the same sound level. Measuring Threshold At each level there is a certain probability associated with responding correctly (yes or no depending on whether the sound is present or not). If we present several repeated presentations at each level we can calculate the probability of a correct response. If we plot this probability against stimulus level we have a “psychometric function.” Measuring Threshold Psychometric functions give a comprehensive description of how detectability changes with level. However, usually a certain probability is chosen as the threshold (e.g. 50% or 75% correct). BSA audiometry procedure defines “threshold” as the level corresponding to 50% correct responses (for rising stimulus levels). A listener with low threshold has high sensitivity. Forced-Choice Task For a PTA type task (yes/no) the probability of a correct answer varies from 0% to 100%. An alternative is to give two possible observation intervals (usually indicated by lights). The subject then has to indicate which interval contained the signal – a two-interval, twoalternative forced choice (2I2AFC) task. Here there is a 50% chance of guessing so the psychometric functions run from 50% to 100% with a certain value, say 75% correct, taken as the threshold. Psychometric Functions at Different Frequencies Other alternatives used in psychophysics (usually automated) include: 3AFC, 33% chance of guessing correct Threshold Level Adaptive tracking e.g. “2-down, 1-up” where two consecutive correct responses are required before the task gets harder and one wrong before it gets easier: trial number Threshold of Audibility Two basic methods have been used to define the threshold of audibility: Minimum audible field (MAF) Minimum audible pressure (MAP) Minimum Audible Field (MAF) Absolute thresholds for free-field tones: presented over a loud speaker in an anechoic environment. Usually with listener facing source 1 m away. Binaural listening (both ears). Listener removed and calibrated microphone placed at the position of listener’s head to calibrate sound field. Calibration doesn’t account for torso, head, and outer-ear diffraction effects which are there in the actual measurements. MAF Free-field threshold of hearing 120 100 dB SPL 80 60 40 20 0 -20 10 100 1000 Frequency (Hz) 10000 100000 Minimum Audible Pressure (MAP) Sound usually delivered by headphones. Monaural measurements. Thresholds described in terms of SPL at listener’s tympanic membrane. SPL measured at eardrum using probe-microphone placed very close to eardrum. Head diffraction and ear canal resonance effects not taken into account in the threshold measurements. MAF vs. MAP The MAP measured with headphones is typically 5-10 dB higher than binaurally measured MAF. 2-3 dB of this difference can be accounted for by the use of two ears rather than one. MAF includes the effect of reflections from the listener’s head and shoulders; measuring MAP with headphones does not. MAF includes ear-canal resonance, MAP does not. It is also likely that physiological noise “trapped” in the ear-canal by the headphones also contributes to this difference at low frequencies (Moore, 2012). Ear canal resonance at 3-4 kHz results in an increase in SPL at the ear-drum relative to that measured with the head removed (MAF). With MAP the SPL is already measured at the ear-drum, so the ear canal resonance effect is removed. Auditory Sensitivity 20-20,000 Hz is the range of frequencies over which the human ear is generally accepted to “hear” sounds. The ear is most sensitive over the 1-6 kHz range. At 1 kHz, normal threshold is about 0 dB SPL or 20 μPa. At this sound level the tympanic membrane is vibrating through a distance less than a tenth the diameter of a hydrogen atom… Auditory Sensitivity – Low Frequencies The true limit of low frequency hearing is about 20 Hz. Below this the necessary sound level is so intense that it may actually be felt rather than heard. Also, low frequency sounds may be detected by higher frequency distortion components rather than the low-frequency components themselves. Auditory Sensitivity – High Frequencies The upper frequency limit of hearing is about 20 kHz. Young children can often hear tones as high as 20 kHz. However, for most adults the threshold rises rapidly above 15 kHz. dB Hearing Level (HL) If we turn the threshold graph upside down and plot the normal threshold of hearing as a straight line, we can obtain a new scale: dB HL (hearing level). 0 dB HL represents average normal hearing at all frequencies. Threshold of Hearing (dB HL) -20 0 dB HL 20 40 60 80 100 100 1000 Frequency (Hz) 10000 dB Sensation Level (SL) dB sensation level is the number of decibels above a person's threshold for a given signal. E.g. a person has a 1 kHz pure-tone threshold of 40 dB SPL, a 1 kHz tone is presented at 60 dB SPL… …the tone is at 20 dB SL, i.e. 20 dB above the person's threshold. Signal Duration and Threshold All these threshold values apply for relatively long signals (~500 ms plus). If we are interested in how signal duration affects signal threshold we can either: Keep the signal power constant. or Keep the signal energy constant. Power = Energy/Time. Signal Duration and Threshold Constant energy: power is decreased as duration increases power time Constant power power time Signal Duration and Threshold Thresholds plotted relative to the threshold for a duration of 1024 ms: Signal Duration and Threshold Above about 250-500 ms the threshold changes little. Below about 250 ms the power must be increased as the tone is made shorter. Signal Duration and Threshold Below about 250-300 Hz we can approximate the ear as a constant energy detector (only approximately). A 10 fold decrease in duration requires a 10 dB increase in power to maintain detection: 10 dB increase in power = 10-fold increase i.e. 10 log10(10/1) = 10 dB For sounds with durations below 10 ms much larger increases in power are required. Implications in audiometry – presentations of 1-3 s duration. Temporal Integration This process has been modelled as “temporal integration.” A signal must contain a critical amount of energy to be detected. If the signal is short it must have a higher intensity (power) to be detected. If the signal is longer a lower power is required. Once a critical duration (about 300 ms) is reached the integration is complete. If the total energy is below that required then the sound isn’t detected. Temporal Integration power Integration time time Loudness Loudness Loudness is the sensation (i.e., a subjective attribute) related to the intensity of a sound. Loudness is a perceptual characteristic, not a physical characteristic of a sound (such as amplitude, intensity etc.). Measurement of Loudness Two main methods of quantifying loudness: Loudness matching - adjust level of target sound so that it matches loudness of comparison sound. Loudness scaling – present target sound and ask subject to assign numerical value to loudness (magnitude estimation), or to adjust loudness of sound to match a given number (magnitude production). Loudness Matching Example The test tone and a 1 kHz tone presented alternately. Listener is asked to adjust the level of the test tone until the two sounds are perceived as being equally loud. Procedure is repeated with test tones of different frequencies and a fixed level reference tone. Repeated for different level reference tones. Equal-Loudness Contours Equal-loudness contours can be mapped out: any two points on a given contour are perceived as having the same loudness. Loudness level in phons is level (in dB SPL) of 1-kHz reference tone that appears equally loud. E.g. sounds equal in loudness to a 40-dB SPL 1-kHz pure tone have a 40 phon loudness level etc. Equal-Loudness Contours Loudness Level in Phons Loudness Scales On the basis of loudness scaling methods Stevens (1957) suggested that for sounds above 40 dB SPL loudness (L in sones) was a power function of intensity (I) such that: L = kI0.3 (where k is a constant) What does this mean? Loudness function is not linear, but is compressive. A 10-fold increase in intensity (+10 dB) approximates to a doubling in loudness. 10 dB increments: BM Response Growth The healthy BM shows a shallow, compressive, growth with level for a tone at CF. 80 dB input range is squashed into a 20 dB output range: 80 f = CF, compressive response BM Velocity (dB) 70 60 50 40 30 10 kHz 8 kHz 3 kHz 20 10 0 0 10 20 30 40 50 60 70 Level (dB SPL) 80 90 100 110 120 Loudness & BM Nonlinearity The shallow growth of loudness with level is a direct consequence of the compressive BM response function. In fact, loudness in sones is approximately proportional to the square of BM velocity (in other words, loudness is proportional to the intensity of BM vibration). Loudness Recruitment Effects of Cochlear Hearing Loss: Loudness Recruitment Dysfunction of OHCs leads to loss of active mechanism that produces compression. Hence, loudness grows much more rapidly with increasing sound level than normal (loudness recruitment). Response Functions The shallow response growth, and sensitivity, goes away if the cochlea is in a poor physiological condition: Gain ≈ 50 dB Ruggero et al. (1997) Loudness Recruitment 5 Normal Loudness Rating 4 Cochlear Loss 3 2 1 0 0 20 40 60 Level (dB SPL) 80 100 Binaural Loudness Matching For listeners with a unilateral loss, recruitment in the impaired ear can be measured by loudness matching with the good ear. Medium-level tones in the impaired ear may sound as loud as low-level tones in the normal ear. However, the same high-level tone might be judged equally loud in the normal and impaired ears. Loudness Scaling Similar results can be obtained for loudness scaling experiments. In this experiment, listeners had to rate the loudness of sounds on a five-point scale (1 = “very soft”, 5 = “very loud”). dashed lines indicate normal hearing S1 and S2 both show recruitment S3 shows no recruitment conductive loss? Temporal Masking Curves Masker Interval 2.2 kHz 4 kHz 4 kHz Time Frequency Frequency Masker Level (dB SPL) Signal Masker-Signal Interval (ms) A given increase in masker-signal interval has a larger effect on the masker level required at medium masker levels: (dB) BM BM Velocity Velocity (dB) 60 50 40 30 20 10 0 0 10 20 30 40 50 60 70 Masker Level (dB Sound Pressure LevelSPL) (dB) 80 90 100 Masker Level (dB SPL) Temporal Masking Curves Masker-Signal Interval (ms) Masker Level (dB SPL) Temporal Masking Curves Masker-Signal Interval (ms) 2.2-kHz Masker Level (dB SPL) Derived basilar-membrane input/output function: 4-kHz Masker Level (dB SPL) Response functions at 4 kHz derived from TMCs for normalhearing listeners (Plack et al., 2004, JASA 115, p. 1684): Response functions at 4 kHz derived from TMCs for listeners with mild-to-moderate cochlear loss: 2200-Hz Masker Level (dB SPL) Fit linear regression functions to estimate the slope of the response function and the gain of the cochlear amplifier: Slope = 0.13 dB/dB Gain = 53 dB 4000-Hz Masker Level (dB SPL) Strong relation between the amount of hearing loss and the maximum gain of the cochlear amplifier: No clear relation between the amount of hearing loss and the maximum compression exponent: Mild-to-moderate cochlear hearing loss: Normal Impaired Moderate-to-severe cochlear hearing loss: Normal Impaired Calculation of OHC and IHC loss: OHC loss = loss of gain Normal Impaired IHC loss = HL - OHC loss Correcting for Loudness Recruitment If the sound is simply amplified for the impaired listener, say by 40 dB, then low-level sounds would be audible, but high level sounds would be unbearably loud! To overcome this, the signal needs compression (to reduce the dynamic range) as well as amplification. This can restore a normal dynamic range, and normal growth of loudness with level. Linear TOO LOUD peak clipping LOUD Intense Moderate LOUD QUIET QUIET Weak Normal Impaired Compression LOUD Intense Moderate LOUD QUIET QUIET Weak Normal Impaired Correcting for Loudness Recruitment The same degree of hearing loss may not be present at all frequencies. Different degrees of amplification and compression may be required at different frequencies to enable speech sounds to be heard comfortably. Hence multi-band compression in digital (and some analogue) hearing aids. Intensity Discrimination Detection of Intensity Changes Intensity discrimination - two or more separate sounds presented successively, one more intense than the others, and the listener indicates which was the more intense: Intensity Discrimination for Wideband Noise Smallest detectable intensity change is approximately a constant fraction of the stimulus intensity. I.e. DI/I is roughly constant. An example of Weber’s law (DI/I is often referred to as the Weber fraction). Weber’s Law Weber's law - the smallest detectable change in a stimulus is proportional to the magnitude of that stimulus. In dB, the smallest detectable change in level is given by: DL = 10 log10[(I+DI)/I] The value of DL is about 0.5 - 1 dB for wideband noise. Holds from about 20 dB above threshold to about 100 dB above threshold for wideband noise. Intensity Discrimination for Pure Tones For pure tones (sinusoids), Weber's law does not hold. DI/I decreases with increasing I. This is referred to as the "near miss to Weber's law." Auditory Sensitivity & Loudness • Learning Outcomes – Understand how auditory sensitivity can be measured – Understand what is meant by MAF and MAP – Understand how and why threshold depends on signal duration – Understand how loudness is defined and quantified – Understand how loudness is affected by hearing loss – Understand the basic intensity sensitivity of the human ear


















































































![lect2-8 [Compatibility Mode]](http://s1.studyres.com/store/data/001740546_1-c501c5e94892aeeec505c370410f58c0-150x150.png)