Download lecture14

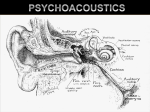
Loudness level (phon)
An equal-loudness contour is
a measure of sound pressure
(dB SPL), over the frequency
spectrum, for which a listener
perceives a constant loudness
when presented with pure
steady tones.
Equal Loudness Curves
Hearing sensitivity is maximum
near the first resonant frequency
3.5 - 4.0 kHz of the outer ear
canal, and has another peak at
the second resonance ~13kHz
Phon is equal to the sound
pressure level in decibels
at f = 1 kHz
The unit of measurement for loudness levels is the phon, and is arrived at by reference
to equal-loudness contours. By definition two sine waves, of differing frequencies, are
said to have equal-loudness level measured in phons if they appear equally loud to the
average young person without significant hearing impairment.
1
2
Loudness of pure tones (sone)
Loudness S in sones:
S  2  LL  40 / 10
Loudness level in phones: L L
sone
1
2
4
8
16
32
64
128
256
512
1024
phon 40
50
60
70
80
90
100
110
120
130
140
One sone is the loudness of a 1 kHz tone at a sound level of 40 dB
(loudness level 40 phons)
Loudness level (see previous slid) has been constructed using sound
pressure level, which is logarithmic function of intensity. Because of that
loudness level is slow function of intensity. Sone has been introduced to
“return beck “
• Loudness level and sone are based on the average listener sensation
of loudness.
• Sound pressure level and intensity are independent on the listener
sensation.
3
Musical dynamics and loudness
Dynamic range: the range of sound level in musical performance
4
Loudness and Masking
When the ear is exposed to two or more different tones, one can mask the
other.
Example: Hearing threshold of the weaker tone is shifted up by the louder tone
1. Pure tones close together in frequency mask each other more then tones
widely separated
2. Pure tone masks tones of higher frequency more effectively then tones of
lower frequency
3. The grater intensity of the masking tone, the broader the range of
frequencies it can mask
4. Forward masking – masking of a tone by a sound that ends a short time
(~ 20 – 30 ms) before tone begins (recently stimulated cells are not as
sensitive as fully rested cells)
5. Backward masking – a tone can be masked by a noise that begins up to
10 ms later
6. Narrow band masking is similar to pure tone masking
7. Broad band (white) noise masking approximately linearly increase with
the noise level
5
8. Noise in one ear can mask tone in the other ear
Loudness and duration: impulsive sounds adaptation
•Ear averages sound energy over about 0.2s
(so loudness grows with duration up to this value)
•Acoustic reflex
- Ear has protection against very loud sound (above 85 dB) and sudden
pressure changes.
- It is protected by muscles attached to eardrum and the ossicles of the
middle ear. They tightens the eardrum and move stirrup-shaped bone away
from the oval window.
- The reflex does not begin until 30-40 ms after sound overload occurs.
•Adaptation – sensation decrees with prolonged stimulation (small effect)
•Auditory Fatigue (a temporary threshold shift) – laud sound effects
ability to hear another sound at a later time. In extreme situation: a
temporary loss of hearing after exposure to sound.
6
Fourier analysis
Any periodic vibration, however, complicated, can be built up from a series
of simple vibrations, whose frequencies are harmonics of a fundamental
frequency, by choosing the proper amplitudes and phases of these
harmonics.
Compare this mathematical statement with the fact that practically any
music can be played on piano.
Periodic function: F t  T   F t 
F t  
A
n 1, 2...
n
sin  n t   n 
T is period
f1 = 1/T is fundamental frequency
n  2f n  2nf1  2n / T
•Fourier analysis – the determination of harmonic component of a periodic function
•Fourier Synthesis - the construction of a complex function from its harmonics
(the opposite of Fourier analysis)
7
sin t 
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
sin 2t 
0
0.5
1
1.5
2
2.5
3
3.5
4
0
0.5
1
1.5
2
2.5
3
3.5
4
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
sin 3t 
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
8
-0.8
-1
0
0.5
1
1.5
2
2.5
3
3.5
4
Spectrum - specification of the strengths of the various harmonics
Examples:
•A square wave has a spectrum with a fundamental followed by odd
harmonics with the ratio of the amplitudes being 1/n
•A triangle wave has a spectrum with a fundamental followed by odd
harmonics, but the ratio of the amplitudes is 1/n2
•A saw tooth wave has a spectrum with both odd and even harmonics and
amplitude ratio of 1/n2
1
Square wave
0.8
0.6
An
0.4
0.2
0
-0.2
f
1 3 5 7
-0.4
-0.6
-0.8
-1
0
0.5
1
1.5
2
2.5
3
1
  sin nt 

n 1, 2... 7  n 
  2f
3.5
4
9
1
  sin nt 

n 1, 3,  n 
1
  sin nt 

n 1, 3, 5  n 
1
1
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
0
0
-0.2
-0.2
-0.4
-0.4
-0.6
-0.6
-0.8
-0.8
-1
0
0.5
1
1.5
2
2.5
3
3.5
4
-1
0
1
  sin nt 

n 1, 3, 5, 7  n 
0.5
1
1.5
2
2.5
3
3.5
4
1
  sin nt 

n 1, 3, 5, 7 , 9  n 
1
1
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
0
0
-0.2
-0.2
-0.4
-0.4
-0.6
-0.6
-0.8
-0.8
-1
-1
0
0.5
1
1.5
2
2.5
3
3.5
4
10
0
0.5
1
1.5
2
2.5
3
3.5
4
 sin nt 
 1 
 2  sin nt 

n 1, 3, 5, 7 , 9  n 
n 1, 2... 9
8
1
6
0.8
0.6
4
0.4
2
0.2
0
0
-2
-0.2
-0.4
-4
-0.6
-6
-8
-0.8
-1
0
0.5
1
1.5
2
2.5
3
3.5
4
0
0.5
1
1.5
2
2.5
3
3.5
4
 sin nt 
n 1, 3, 5, 7 ,. 9
4
3
2
1
0
-1
-2
-3
-4
11
0
0.5
1
1.5
2
2.5
3
3.5
4
Comments about spectra of musical instruments
The spectra for musical instruments vary depending on:
•the way in which the instrument is played (soft, loud, high, low or midrange)
•how the sound is recorded (near field, far field, reverberant field, direction of
microphone from the instrument)
•Typical spectra of voiced instruments (such as a violin, trumpet, guitar)
have sharply defined peaks
•The spectra of unvoiced instruments (such a drums) have a broadband
of frequency responses with no clearly defined peaks
12