Download How Tall is This?

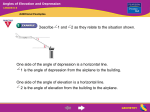
Things Are Looking Up!
Objective:
Indirect Measurement of Height Using Right Triangles
Prerequisite skills:
Trig Definitions
Solve Trig Equations
Tools:
Clinometer
Measuring Tape
Calculators
• CA Standards (18.0 & 19.0):
Students know the definitions of the basic trigonometric functions defined by the angles of a right triangle
Students use trigonometric functions to solve for an unknown length of a side of a right triangle, given an
angle and a length of a side
• Core Geometry G-SRT (6 & 7):
Define trigonometric ratios and solve problems involving right triangles.
• Core Math Practices
MP.1 - Make sense of problems and persevere in solving them.
MP.4 - Model with mathematics.
MP.5 - Use appropriate tools strategically.
MP.6 - Attend to precision.
Mt. Everest
• What do you know about this mountain?
• Estimate the height of Mt. Everest .
• What word represents height in terms of a mountain?
Mt. Everest History
• On May 29th 1953, Sir Edmund Hilary and his guide
Tenzing Norgay were the first people to ascend to the
peak of Mt. Everest, the highest elevation in the world.
• How do you think Mt. Everest’s elevation was calculated?
Let’s Consider……
• A Mountain with Vertical Height
Mt. Rushmore National Monument
Black Hills, South Dakota
Completed in 1941
Estimate the Elevation.
How Do I Use Trigonometry for
Indirect Measurement?
• Write any observations made from the
picture. Draw a sketch if needed.
How Do I Find the Height of Tall Objects Using
Trigonometry?
• What measurements are needed?
• How would I calculate the tall object’s height?
Height
𝒙°
Eye Height
Distance to Object
Indirect Measurement Reflection
Explain how trigonometry is used for indirect
measurement of height. Consider the following:
• Measurements that are Needed
• Visual Representation
• Proper Use of Vocabulary
Act 2: Experiencing Indirect Measurement
• Clinometer: An instrument used by surveyors
in order to measure an angle of elevation or
depression
Measures Slope Angle From Horizontal Line
Making Your Own Clinometer
• Template
• Protractor
Using Your Clinometer
• Line of Sight to Object
• Angle Measures: From Horizontal Eye Height
Partner Practice: Ceiling & Floor
Clinometer Activity
Task:
Use indirect measurement to find the
height of two tall objects
 Materials: Tape Measure, Clinometer, Calculator
Clinometer Activity
For each object:
• Collect Three Data Sets: Use Different Distances to object
• Draw a diagram with indicated measurements
• Show all calculations that lead to object height
 include appropriate units
• Check for reasonable heights.
Clinometer Activity: Group Roles
 Surveyor: Operates Clinometer
Supervises group to stay on task, time keep
 Technician: Reads Clinometer angle value
Ensures accuracy of all measurements
 Specialist: Measures all distances with tape ruler
Encourages team work
 Recorder: Writes down all data
Manages tools for appropriate use
Clinometer Activity Summary
• Describe the mathematics required to
indirectly measure a tall object’s height.
• Explain any difficulties that may have arisen
in order to complete the task.
• How could we use our Clinometer Activity
experience to calculate a mountain’s
elevation?
Act 3: Viewing Mt. Rushmore
A sightseer is on the Avenue of Flags pathway.
• What information or resources are needed for the sightseer to
calculate the height of Mt. Rushmore from this pathway?
Viewing Mt. Rushmore
• Distance of Sightseer to base of
Mountain (as taken from
picture):
729 feet
• Eye Height of Sightseer:
• Clinometer Reading:
5’7”
𝟔𝟐. 𝟑𝒐
 Find the height of
Mt. Rushmore from
the Avenue of Flags
pathway.
Mt Rushmore Elevation
5725 feet
•
Is height the same as elevation?
Explain.
Viewing Mt. Rushmore
Find the elevation
of the Avenue of
Flags pathway.
Act 4: Revisiting Mt. Everest
Before climbing Mt. Everest, Sir Edmund Hillary and guide
Tensing Norgay wanted to know its vertical height.
At the base of the mountain, Hillary and Norgay
measured a 𝟕𝟗. 𝟔𝟗𝟑𝟒° angle of elevation to the peak.
They were 1 mile away from the altitude.
• Draw a picture to represent their position with respect
to the peak.
• Find the elevation of Mount Everest.
Mt. Everest Elevation
29,035 feet