Download Dr. Math Does Trigonometry

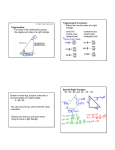
When you have a right triangle there
are 5 things you can know about it..



the lengths of the sides (A, B, and C)
the measures of the acute angles (a and b)
(The third angle is always 90 degrees)
b
C
A
a
B
If you know two of the sides, you can
use the Pythagorean theorem to find
the other side
A  C 2  B2
B  C 2  A2
C
A2  B 2
if A  3, B  4
C
A2  B 2
C  3 4
2
b
C
A=3
2
C  25  5
a
B=4
And if you know either angle, a or b,
you can subtract it from 90 to get the
other one: a + b = 90





This works because there are 180º in a
triangle and we are already using up 90º
For example:
if a = 30º
b = 90º – 30º
b
C
b = 60º
a
B
A
But what if you want to know
the angles?


Well, here is the central insight of
trigonometry:
If you multiply all the sides of a right triangle
by the same number (k), you get a triangle
that is a different size, but which has the
same angles:
k(C)
C
b
a
B
A
b
k(A)
a
k(B)
How does that help us?
Take a triangle where angle b is 60º and
angle a is 30º
 If side B is 1unit long, then side C must be 2
units long, so that we know that for a triangle
of this shape the ratio of side B to C is 1:2
 There are ratios for every
shape of triangle!
C=2

60 º
A=1
30º
B
But there are three pairs of
sides possible!


Yes, so there are three sets of ratios for any
triangle
They are mysteriously named:
sin…short for sine
 cos…short for cosine
 tan…short or tangent


and the ratios are already calculated, you just
need to use them
So what are the formulas?
opp
sin  
hyp
adj
cos 
hyp
opp
tan  
adj
Tan
is
Opposite
over Hypotenuse
Adjacent
Sin is
Cos
isOpposite
Adjacent over
Hypotenuse
SOHCAHTOA
Some terminology:




Before we can use the ratios we need to get
a few terms straight
The hypotenuse (hyp) is the longest side of
the triangle – it never changes
The opposite (opp) is the side directly across
from the angle you are considering
The adjacent (adj) is the side right beside the
angle you are considering
A picture always helps…

looking at the triangle in terms of angle b

A is the adjacent
(near the angle)


C
B is the opposite
(across from the angle)
C is always the
hypotenuse
b
Longest
A
B
hyp
b
Near
adj
opp Across
But if we switch angles…

looking at the triangle in terms of angle a

A is the opposite (across
from the angle)
C
A
a


B is the adjacent (near
the angle)
C is always the
hypotenuse
B
Across
hyp
Longest
opp
a
adj
Near
Lets try an example







Suppose we want to
find angle a
what is side A?
the opposite
what is side B?
the adjacent
with opposite and
adjacent we use
the…
a
tan formula
opp
tan  
adj
b
C
A=3
B=4
Lets solve it
opp
tan  
adj
3
tan a   0.75
4
check our calculators
a  36.87º
b
C
A=3
a
B=4
Another tangent example…




we want to find angle b
B is the opposite
A is the adjacent
so we use tan
4
tan b 
3
tan b  1.33
b  53 .13 
opp
tan  
adj
b
C
A=3
a
B=4
Calculating a side if you know
the angle


you know a side (adj) and an angle (25°)
we want to know the opposite side
A
tan 25  
6
A  tan 25   6
A  0.47  6
A  2.80
opp
tan  
adj
b
C
A
25°
B=6
Another tangent example

If you know a side and an angle, you can
find the other side.
6
tan 25  
B
6
B
tan 25 
6
B
0.47
B  12 .87
opp
tan  
adj
b
C
A=6
25°
B
An application



You look up at an angle of 65° at the top of
a tree that is 10m away
the distance to the tree is the adjacent side
the height of the tree is the opposite side
opp
tan 65  
10
opp  10  tan 65 
opp  10  2.14
opp  21 .4
65°
10m
Why do we need the sin & cos?




We use sin and cos when we need to work
with the hypotenuse
if you noticed, the tan formula does not have
the hypotenuse in it.
so we need different formulas to do this work
sin and cos are the ones!
C = 10
b
A
25°
B
Lets do sin first


we want to find angle a
since we have opp and hyp we
use sin
5
sin a 
10
sin a  0.5
a  30 
C = 10
opp
sin  
hyp
b
A=5
a
B
And one more sin example


find the length of side A
We have the angle and
the hyp, and we need
the opp
A
sin 25  
20
A  sin 25   20
A  0.42  20
A  8.45
opp
sin  
hyp
C = 20
b
A
25°
B
And finally cos


We use cos when we need to work with the
hyp and adj
adj
cos 
so lets find angle b
4
cos b 
10
cos b  0.4
b  66 .42 
hyp
C = 10
b
A=4
a
a  90  - 66.42 
a  23.58 
B
Here is an example




Spike wants to ride down a steel
beam
The beam is 5m long and is
leaning against a tree at an angle
of 65° to the ground
His friends want to find out how
high up in the air he is when he
starts so they can put add it to the
doctors report at the hospital
How high up is he?
How do we know which
formula to use???





Well, what are we working with?
We have an angle
We have hyp
We need opp
With these things we will use B
the sin formula
C=5
65°
So lets calculate
opp
sin 65  
hyp
opp
sin 65  
5
opp  sin 65   5
opp  0.91  5
opp  4.53

so Spike will have fallen 4.53m
C=5
B
65°
One last example…



Lucretia drops her walkman
off the Leaning Tower of
Pisa when she visits Italy
It falls to the ground 2
meters from the base of the
tower
If the tower is at an angle of
88° to the ground, how far
did it fall?
First draw a triangle





What parts do we have?
We have an angle
We have the Adjacent
We need the opposite
Since we are working with
the adj and opp, we will use
the tan formula
B
88°
2m
So lets calculate
opp
tan 88  
adj
opp
tan 88  
2
opp  tan 88   2
opp  28 .64  2
opp  57 .27

Lucretia’s walkman fell 57.27m
B
88°
2m
What are the steps for doing
one of these questions?
1.
2.
3.
4.
5.
6.
7.
Make a diagram if needed
Determine which angle you are working
with
Label the sides you are working with
Decide which formula fits the sides
Substitute the values into the formula
Solve the equation for the unknown value
Does the answer make sense?
Two Triangle Problems




Although there are two triangles, you only
need to solve one at a time
The big thing is to analyze the system to
understand what you are being given
Consider the following problem:
You are standing on the roof of one building
looking at another building, and need to find
the height of both buildings.
Draw a diagram

You can measure
the angle 40° down
to the base of other
building and up 60°
to the top as well.
You know the
distance between
the two buildings is
45m
60°
40°
45m
Break the problem into two
triangles.

The first triangle:
a
60°

The second triangle
45m
40°


note that they share
a side 45m long
a and b are heights!
b
The First Triangle


We are dealing with an angle, the opposite
and the adjacent
this gives us Tan
a
tan 60  
45
a  tan 60   45
a  1.73  45
a  77.94m
a
60°
45m
The second triangle


We are dealing with an angle, the opposite and
the adjacent
this gives us Tan
b
tan 40  
45
b  tan 40   45
b  0.84  45
b  37.76m
45m
40°
b
What does it mean?



Look at the diagram now:
the short building is
37.76m tall
the tall building is 77.94m
plus 37.76m tall, which
equals 115.70m tall
77.94m
60°
40°
37.76m
45m