* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download VU2 Light 2009
Survey
Document related concepts
Transcript
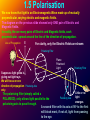
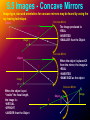
VCE Physics Unit 2 Topic 2 Wave Like Properties of Light View physics as a system of thinking about the world rather than information that can be dumped into your brain without integrating it into your own belief systems. Unit Outline • • • • • • • • • • Describe transverse waves in terms of amplitude wavelength period and frequency Calculate wavelength, frequency, period and speed of travel of light waves, v = fλ = λ/T Investigate and analyse the behaviour of light using ray diagrams including reflection, i = r refraction, Snell’s Law total internal reflection, critical angle (any form of image location is not required) Describe light using a wave model and a particle model. Explain polarization of visible light and its relation to a transverse wave model Compare the wave model and the particle model of light in terms of whether they adequately describe reflection and refraction. Identify visible light as a particular region of the spectrum of electromagnetic radiation and that all light travels at the speed of light in a vacuum, c. Explain the colour components of white light as different frequencies of light combining to appear white. Explain colour dispersion in prisms and lenses in terms of refraction of the components of white light as they pass from one medium to another Identify and apply safe and responsible practices when working with light sources and optical devices Chapter 1 - Waves This chapter covers the following topics: •Wave Behaviour •Wave types: Transverse and Longitudinal •Electromagnetic Radiation •The Medium •Polarisation 1.0 Wave Behaviour There are many types of waves all of which have one common feature:They TRANSFER ENERGY from one place to another. Some waves (eg. Sound, or Water Waves) need a MEDIUM through which to travel. The MEDIUM (eg. air, water), although disturbed by the passage of the waves, does NOT suffer any PERMANENT DISTORTION due to the waves’ movement through it. Other waves, eg light waves, microwaves and X rays don’t require a medium and are so called “self perpetuating” waves. In cases where waves require a medium, it is important to note that the waves does not drag the medium along with it. The sea does not build up along the shore as the waves break !!!!! 1.1 Wave Types - Transverse There are two basic types of waves: TRANSVERSE WAVES. LONGITUDINAL WAVES. 1. TRANSVERSE WAVES are characterised by having the individual particles of the medium through which the wave travels, moving at right angles to the direction of motion of the wave. Direction of motion of the medium’s particles Direction of motion of wave Notice the “medium” does not move along with the wave. Pick a spot and follow its motion. 1.2 Wave Types -Longitudinal 2. LONGITUDINAL WAVES are characterised by having the individual particles which make up the medium through which the wave travels, moving parallel to the direction of motion of the wave. Individual particles of Medium Direction of Wave Motion Direction of Motion of Particles of Medium Pick a point in the medium and follow its progress. Note that it does not move along with the wave, but it is only displaced from its initial position, returning to its original position after the wave has passed. 1.3 Wave Types – Electromagnetic Radiation • • • Light is a form of ENERGY. It is described as ELECTRO - MAGNETIC RADIATION (EMR). EMR is a self propagating wave consisting of mutually perpendicular, varying ELECTRIC and MAGNETIC FIELDS. Changing Magnetic Field Direction of Electromagnetic Wave Movement Changing Electric Field •EMR travels through a vacuum at 300,000 kms-1, (3.0 x 108 ms-1) and only slightly slower in other mediums eg., air, water or glass In a single uniform medium (eg air or glass or water or plastic), the EM waves travel IN A STRAIGHT LINE. 1.4 The Medium •A “MEDIUM” is any Transparent or Translucent material which allows light to pass through it. •Light and, in fact, all E-M waves, DO NOT require a medium for travel. •In the absence of a medium (ie. travelling through a vacuum), Light, and all E-M waves, travel at 300,000 km/s (3.0 x 108 ms-1). •However, when travelling through a medium, Light and all E-M waves will travel at speeds less than 300,000 km/s (3.0 x 108 ms-1). •In a single, uniform medium (eg. air, plastic, glass, water) Light, and all E-M waves, travel IN STRAIGHT LINES. Introduction 1. A common feature of all waves is that A: They all transfer energy from one place to another B: They all require a medium for propagation C: They carry the medium along with them D: They permanently distort the medium through which they travel 2. There are two main types of waves. They are known as A: Transverse and Long B: Travelling and Longitudinal C: Square and Perpendicular D: Transverse and Longitudinal 3. Light is a form of EMR, which means light is A: Electric Magnetic Readings B: Electromagnetic Radiation C: Electron Miniature Rendition D: Electromagnetic Readings Introduction 2 4. Light travelling through a translucent material suffers a 50% reduction in its speed. Its speed through the material is A: 3.0 x 108 ms-1 B: 1.5 x 104 ms-1 C: 1.5 x 108 ms-1 D: 3.0 x 104 ms-1 5. Our ability to reach out and grasp an object in our hand depends upon which one or more of the following properties of light A: Light is made up of a series of colours added together B: Light travels in straight lines C: Light travels at 3.0 x 108 ms-1 D: Light is a form of radiation 1.5 Polarisation We now know that light is an Electromagnetic Wave made up of mutually perpendicular, varying electric and magnetic fields. The diagram on the previous slide showed only ONE pair of Electric and Magnetic fields. In reality, the are many pairs of Electric and Magnetic fields, each perpendicular, spread around the line of the direction of propagation. Line of Propagation E For clarity, only the Electric Fields are shown Polarising Filter Plane Polarised Light Polarising Filter Suppose a light globe is giving out light rays. We will focus on one direction of propagation Polarising Axis only. Little or no The polarising filter (simply called a light Polarising Axis POLARIOD), only allows light parallel to the emerges polarising axis to pass through. A second filter with its axis at 90o to the first will block most, if not all, light from passing to the eye. Chapter 2 This chapter covers the following topics: • Amplitude • Frequency • Period • Wavelength • Speed • Rays and Shadows 2.0 Wave Properties. Amplitude • Amplitude is a measure of the size of a disturbance above or below a mean or average value. Distance Amplitude Mean or Average Value Point of Max. Displacement above the mean or average position Time Point of Max. Displacement below the mean or average position 2.1 Wave Properties. Frequency • • Frequency (symbol f ) is most generally defined as the number of events which occur during a time interval. Distance Low Frequency In terms of Light Waves it represents the number of complete light waves passing a given point in a given time. • In the SI system, frequency is defined as the number of events or cycles per second. • The UNIT for frequency is the HERTZ (Hz), where 1 Hz = 1 cycle per second Time High Frequency 2.2 Wave Properties. Period D • Time • 0.02 Period (T) = 0.02 s f = 1/T = 1/0.02 = 50 Hz 0.04 Period (symbol T) is defined as the time it takes for one event to occur. It is the time it takes for one complete light wave to pass a given point. • Period is the measure of a time interval, thus has the unit seconds (s). • Period and frequency are the inverse of one another thus: f 1 T Thus, a wave of period 0.02 s has a frequency of 50 Hz 2.3 Wave Properties. Wavelength • • • Wavelength, (symbol , Greek Letter LAMBDA), is a measure of the distance between two adjacent points on a wave undergoing similar motions. Thus the distance between two adjacent compressions or two adjacent rarefactions would be 1 wavelength. Wavelength is a distance measure, hence the unit for is metres (m). Compression Rarefaction Transverse Wave Longitudinal Wave Compression Rarefaction 2.4 Wave Properties. Wave Speed • Wave Speed (symbol v) is a measure of how quickly a “wavetrain” is moving. • The wave speed is dependent on the frequency and wavelength of the wave train. • The relation is summarised in the so called “WAVE EQUATION”, v = f where; v = Speed (ms-1), f = Frequency (Hz) = Wavelength (m). •This is a most important equation used in many areas of the course. 2.5 Wave Properties. Shadows When an object is illuminated it casts a shadow. The shadow may have strictly defined edges, a so called, “sharp” shadow, or it may have ill defined edges, a so called “fuzzy” shadow. The factor which decides what type of shadow is produced is the SIZE of Screen the light source. Point Source POINT SOURCES produce sharp shadows. Penumbra Umbra Object EXTENDED SOURCES produce fuzzy shadows.Umbra Object Penumbra Umbra = Region of Full Shadow Penumbra = Region of Partial Shadow (causes the fuzzy edges) Extended Source Wave Formula 6. A wave travelling at 4.52 x 103 ms-1 has a measured frequency of 2.45 x 104 Hz, Calculate its wavelength. v = fλ λ = v/f = (4.52 x 103)/( 2.45 x 104 ) = 0.18 m 7. A wave of frequency 100 Hz will have a period of ? T = 1/f = 1/100 = 0.01 s 8. A ray of red light travelling through a vacuum at a speed of 3.0 x 108 ms-1 has a wavelength of 450 nm. Calculate (a) its frequency and (b) its period. (a) v = fλ f = v/λ = (3.0 x 108)/(450 x 10-9) = 6.67 x 1014 Hz (b) T = 1/f = 1/(6.67 x 1014) = 1.5 x 10-15 s 9. What is the meaning of the terms “umbra” and “penumbra” ? Both terms refer to shadows. Umbra is full shadow, penumbra is partial shadow Chapter 3 This chapter covers the following topics: • Electromagnetic Spectrum • Colour • Colour Mixing • Transparent Materials • Opaque Materials 3.0 The Electromagnetic Spectrum The ELECTROMAGNETIC SPECTRUM encompasses all ELECTROMAGNETIC RADIATION of which VISIBLE LIGHT is but a small part. Frequency, f (Hz) 1024 1022 1020 1018 1016 1014 1012 108 1010 Gamma rays High Energy UV 10-14 Microwaves X Rays Cosmic Rays 10-16 Infra Red 10-12 10-10 In a vacuum, all EM Radiation travels at the same speed : v = 3.0 x 108 ms-1 λVIOLET = 4.5 x 10-7 m = 450 nm 10-8 10-6 10-4 Wavelength, λ (m) 10-2 TV 100 106 104 Radio Waves 102 Low Energy 104 1 nm = 10-9 m Visible Light λRED = 7.5 x 10-7 m = 750 nm Notice how small the range of wavelengths is for the visible region of the E-M Spectrum. This small range of wavelengths give us our ability to “see” the world. Imagine how much more complex the world be if our eyes were able to “see” all the wavelengths of the electromagnetic spectrum. 3.1 Colour The fact that “white” light is made up of a mixture of colours was first discovered by Isaac NEWTON (1642 - 1727). When Newton passed white light through a triangular prism, it was broken up into its constituent colours. This “break up” occurs because This process is called DISPERSION each colour has a slightly different wavelength and when passed through the prism suffers White Light a slightly different change in Red Orange direction. Yellow Green Colours associated with definite Blue wavelengths are called Indigo SPECTRAL COLOURS. Violet The colours and their wavelengths: Colour RED ORANGE YELLOW GREEN BLUE INDIGO VIOLET Wavelength (nm) 650 600 580 550 500 470 450 From both the diagram and the table, it should be obvious that the shorter the wavelength, the greater the change in direction. Electromagnetic Radiation 10. Arrange the following examples of EMR from shortest to longest wavelength Cosmic rays, Radio waves, Visible light, Gamma rays, Ultraviolet, Microwaves, Infrared, X Rays, TV. Cosmic rays, Gamma rays, X Rays, Ultraviolet, Visible light, Infrared, Microwaves, TV, Radio waves. 11. Why can a prism split white light into is component colours ? The reason that this break up occurs is because each colour has a slightly different wavelength (or frequency which ever term you want to use) and because of this each suffers a slightly different change in direction while passing through the prism. 3.2 Colour Mixing Just as light can be broken up into individual colours, so individual colours of light can be recombined to produce white light. When the various colours of LIGHT are mixed together we can achieve all colours of the rainbow, but more importantly, we can produce white light. This is an ADDITIVE PROCESS. Additive Colour Chart Subtractive Colour Chart However, when paints or pigments are added together , each pigment absorbs, or subtracts, certain colours, so this is a SUBTRACTIVE PROCESS. Thus when every pigment colours is added, all colour will have been absorbed leaving only black. 3.3 Colour: Transparent Materials There are 3 basic types of materials in the world. TRANSPARENT objects transmit most light reflecting and absorbing very little. TRANSLUCENT objects transmit some light (usually distorted) while reflecting and absorbing more of the light than transparent materials. OPAQUE objects transmit no light and reflect and /or absorb all light. TRANSPARENT OBJECTS which are coloured (usually called FILTERS) transmit their colour whilst at the same time absorbing all other colours. Examples of White Light interacting with various filters are shown below. White Light White Light Red Light Red Filter Blue Filter White Light Red Light No Light Emerges Red Filter Blue Filter Blue Light 3.4 Colour: Opaque Materials Examples of White Light interacting with various OPAQUE MATERILALS are shown below. White Light White Light White Light Red Light White Light Red White White Light Blue Light Blue White Light Red Light Blue Light No reflected Light Black Purple Opaque objects appear coloured because they reflect their colour while, at the same time, absorbing all other colours. Colour 12. How is the process of adding light different from the process of adding pigments ? When the various colours of light are mixed together we can achieve all colours of the rainbow, but more importantly, we can produce white light. This is an ADDITIVE PROCESS. However, when paints or pigments are added together, each pigment absorbs, or subtracts certain colours, so this is a SUBTRACTIVE PROCESS. 13. As far as light is concerned there are 3 types of materials in the world: Draw a line between the term and its meaning Term Transparent Translucent Opaque Meaning materials transmit some light (usually distorted) while reflecting and absorbing more of the light than other materials. materials transmit no light and reflect and/or absorb all light. materials transmit most light reflecting and absorbing very little. Colour and Filters 14. Why is a blue tee shirt blue to an observer ? Blue tee shirts are blue because the blue fabric absorbs all colours except blue which it reflects. 15. Describe how you could use 2 simple filters to block out all visible light Shine light firstly through a blue filter leaving only blue light, then shine that onto a red filter, no light will emerge from the red filter. Chapter 4 This chapter covers the following topics: • Reflection • Refraction • Index of Refraction • Critical Angle • Total Internal Reflection • Optical Fibres • Interference Patterns 4.0 The Properties of Light Reflection Before studying the Laws of Reflection the idea of a NORMAL needs to be introduced. The NORMAL The NORMAL is an imaginary line drawn at Right Angles to the Reflecting Surface. It is used to define the angles of incidence and reflection. Reflecting Surface THE LAWS OF REFLECTION Incident Ray Reflected Ray i r Reflecting Surface i = Angle of Incidence r = Angle of Reflection 1. Angle of Incidence = Angle of Reflection 2. The Incident Ray, the Reflected Ray and the Normal are COPLANER (all lie in the one plane) and all lie on the same side of the reflecting surface. 16. What is a Normal ? Reflection The Normal is an imaginary line perpendicular to the reflecting or refracting surface. 17. Two plane mirrors are set up as shown a ray incident on the lower mirror reflects onto the upper one. Determine the values of the angles marked W, X, Y and Z. Mirror Z Normal W = 600; X = 600; Y = 300; Z = 600 Y X W 300 100 Mirror 1000 4.1 The Properties of Light Refraction Refraction is the changing of the direction of travel of a light ray which generally occurs when light passes from one medium to another (eg when passing from air to glass). The reason for the change in direction is that THE SPEED OF LIGHT changes when passing into the new medium. The speed is inversely proportional to the density of the medium, ie. The slower the speed, the denser the medium. Incident Ray Incident Ray Air Normal i Glass r i = Angle of Incidence r = Angle of Refraction Refracted Ray Note: If the incident ray is directed in along the Normal, it will NOT change its direction when it crosses the boundary. For other directions a change in direction WILL occur. Since DensityGLASS > DensityAIR it can be seen that in travelling from a less dense to a more dense medium the light ray is refracted TOWARD the Normal. 4.2 The Properties of Light The Laws of Refraction THE LAWS OF REFRACTION. The first law of refraction is also known as SNELL’S LAW Incident Ray Air Normal i Glass r i = Angle of Incidence 1. Snell’s Law. For a given pair of media, the ratio of the Sine of the angle of Incidence to the Sine of the angle of Refraction is a constant (n). Mathematically: Sin i/Sin r = n n is called the “Index of Refraction” or more simply the “Refractive Index” r = Angle of Refraction Refracted Ray 2. The Incident Ray, the Refracted Ray and the Normal to the refracting surface at the point of incidence are COPLANER and the Incident and Refracted Ray are on opposite sides of the refracting surface. 4.3 The Properties of Light The Index of Refraction (1) ABSOLUTE REFRACTIVE INDEX. If one of the media involved in the Refraction process is a VACUUM, the constant, n, in Snell’s Law becomes “THE ABSOLUTE REFRACTIVE INDEX”. Values of the absolute refractive index for various materials are: Note the closeness of the values for Vacuum and Air. In all cases in this Material Absolute Refractive course, nAIR can be taken to be equal to Index nVACUUM = 1.00 Vacuum 1.0000 Air 1.0003 RELATIVE REFRACTIVE INDEX Water 1.33 If neither of the mediums involved in a Oleic Acid 1.46 Quartz 1.46 refraction process is a vacuum, each will Perspex 1.50 have its own Absolute Refractive Index Crown Glass 1.52 and the constant (n) in Snell’s Law must Diamond 2.42 reflect that fact. In general for two mediums with Absolute Refractive Indexes n1 and n2, Snell’s Law becomes: n1Sin i = n2 Sin r Sin i/Sin r = n2/n1 The ratio n2/n1 is usually quoted as n12 and is called the “RELATIVE REFRACTIVE INDEX” for light travelling from medium 1 to medium 2 4.4 The Properties of Light Index of Refraction (2) An example may be useful in understanding “Relative Refractive Index” Normal Plastic nG = 1.50 i Water nW = 1.33 RRI’s less than 1 mean the light is travelling into a less dense medium. r Normal Plastic nG = 1.50 r Water nW = 1.33 i A block of Plastic is floated on water A beam of light passes through the plastic and enters the water. In this situation the Relative Refractive Index (RRI) for light travelling from Plastic to Water, nPW = nW/nP = 1.33/1.50 = 0.89 If the position is reversed and the light travels from the water into the plastic. The Relative Refractive Index for light travelling from Water to Plastic, nWP = nP/nW = 1.50/1.33 = 1.13 RRI’s greater than 1 mean the light is travelling into a more dense medium. Refraction 18. State Snell’s Law in mathematical terms Sin i/Sin r = a constant 19. Calculate the angle of refraction for light passing from air (n = 1.00) at an incident angle of 460 into diamond (n = 2.42) nair Sin i = ndiamondSin r r = Sin-1 (1.00 Sin 46/2.42) = 17.30 20. What is the difference between an absolute refractive index and a relative refractive index ? If one of the media involved in the refraction process is a vacuum, the constant, n, in Snell’s Law is called the “ABSOLUTE REFRACTIVE INDEX”. If neither medium is a vacuum the constant, n, in Snell’s Law is called the “RELATIVE REFRACTIVE INDEX” 21. A beam of light passed from perspex into oleic acid with an angle of refraction of 720 . What was the beam’s incident angle ? noleic acid = 1.46; n perspex = 1.50. Draw a clear, fully labelled diagram of this situation. nperspex Sin i = noleicSin r i = Sin-1(1.46 Sin72/1.5) = 680 4.5 The Properties of Light Critical Angle When light travels from a more dense to a less dense medium (eg. from water to air), it refracts AWAY from the Normal. As the angle of incidence (i) increases eventually a value of i will be reached which produces and angle of refraction of 900. Normal Air nA = 1.00 This angle of incidence is called the CRITICAL ANGLE (iC) rr i iC Water nW = 1.33 The size of the critical angle for this pair of media can be calculated from Snell’s Law nW Sin iC = nA Sin r 1.33 Sin iC =1.00 Sin 900 Sin iC =1/(1.33) iC = 48.80 4.6 The Properties of Light Total Internal Reflection If the angle of incidence increases beyond the Critical Angle, the light ray will no longer leave the denser medium. The surface of the denser medium will act like a plane mirror reflecting the beam back with an angle of reflection equal to the angle of incidence. Normal nA = 1.00 i r nW = 1.33 4.7 The Properties of Light Optical Fibres Optical Fibres are the basis of modern high speed, high volume communication systems allowing telephone systems, Cable Television and interconnected computer systems to operate in an efficient and timely manner. Optical fibres rely on the Total Internal Reflection of a laser beam to transfer information (usually in digital form) from one place to another. Laser Beam Optical Fibre Each time the laser beam reflects off the inner wall of the optical fibre, it suffers attenuation (loses some of its energy), thus, at intervals of about 10 to 20 km along optical fibre, repeater stations are needed to boost the power of the laser beam before it is transmitted further along the fibre. Individual glass optical fibres 4.8 The Properties of Light Double Slit Interference When light of a single wavelength is passed through a pair of closely spaced, narrow slits, an “interference pattern” is produced. This pattern has a series of equally spaced coloured and black bands spread across the screen onto which it is projected. The width of the coloured bands and their spacing depends on the wavelength of the light used. Short wavelength, BLUE light produces a pattern with narrow blue bands which are closely spaced. Long wavelength, RED light produces a pattern with wider red bands which are spread farther apart. Screen Interference Patterns using the same slits This experiment is known as “Young’s Double Slit Experiment” BLUE Light Incident Light RED Light Double Slits Critical Angle 22. Define critical angle. Critical Angle: that angle of incidence that produces an angle of refraction of 900 23. Determine the critical angle (ic) for light travelling from crown glass (refractive index = 1.52) into air. ic = Sin-1(1/1.52) = 41.10 24. What happens to light rays which approach a boundary with a lower refractive index material at an angle greater than the critical angle for that combination ? The rays are totally internally reflected 25. What are Optical Fibres and what is the basis of their operation ? Optical Fibres are flexible glass (or plastic) tubes through which laser light can travel. Their basis of operation is total internal reflection Chapter 5 This chapter covers the following topics: • Image Formation • Plane Mirrors • Curved Mirrors • Lenses • Ray Tracing 5.0 Image Formation Images formed by mirrors or lenses are characterised by a number of properties which need definition. 1. IMAGE TYPE: There are 2 types of images formed by mirrors and lenses; (a) REAL IMAGES, these actually exist and can be projected onto a screen. (b) VIRTUAL IMAGES, these do not actually exist and CANNOT be projected onto a screen. 2. IMAGE ORIENTATION: When compared to the object, the image may be; (a) upright or erect, ie. in the same orientation as the object, or (b) inverted or upside down, ie. opposite in orientation to the object. 3. IMAGE SIZE: When compared to the object the image may be larger than, equal in size to, or smaller than the object. 4. LATERAL INVERSION: This occurs when images are laterally transposed ie. Right becomes left and visa versa. 5.1 Images - Plane Mirrors The eye “expects” light to travel in straight lines. In order to see the top of her head, the lady needs a ray to travel along the path shown. In order to see her chin she needs a ray to travel as shown. Mirror Object Image The “expectation” that light travels in straight lines means she “sees” her image “inside” the mirror, as shown. The image produced by a plane mirror has the following properties: •Virtual •Upright •Laterally Inverted •Equal in size to the object •As far behind the mirror as the object is in front. Image Formation 26. Images produced by mirrors and lenses are classed as either real or virtual, upright or inverted, and larger or smaller or the same size as the object. Write definitions for the underlined words. Real – the light rays actually meet to produce an image that can be projected onto a screen Virtual - the light rays do not actually meet and the image cannot be projected onto a screen Upright – the image is in the same orientation as the object Inverted – the image is upside down when compared to the object 27. How far behind a plane mirror is the image of an object formed ? As far behind the mirror as the object is in front of it. 5.2 Curved Mirrors There are two kinds of curved mirrors: 1. CONCAVE MIRRORS (Converging Mirrors ). These mirrors force parallel incoming rays together at one point after reflection. Concave Mirror Point at which reflected rays actually meet. Called the FOCAL POINT of mirror 2. CONVEX MIRRORS (Diverging Mirrors). These mirrors force parallel incoming rays to diverge from an apparent meeting point behind the mirror. Convex Mirror Apparent meeting point of reflected rays 5.3 Curved Mirrors Properties and Definitions Before proceeding with image determination, a number of terms associated with curved mirrors need to be defined. Concave Mirror R f PA O C A F A = Aperture of Mirror (diameter of reflecting surface) O = Pole of the Mirror (the centre of the reflecting surface) C = Centre of Curvature (centre of the sphere of which the mirror is a part) R = Radius of Curvature (radius of sphere of which the mirror is a part) PA = Principal Axis (a line joining the centre of curvature and the pole of the mirror). f = Focal Point (point at which rays, initially parallel to the principal axis, meet after reflection). F = Focal Length (distance from pole to focal point). 5.4 Ray Tracing – Concave Mirrors In order to determine the position and type of image produced by a concave mirror, a number of “standard” light rays can be used. The three most important are illustrated below: Concave Mirror Object PA Ray 1 Ray 3 f Ray 2 i r Image Ray 1 - A ray, initially parallel to the Principal Axis, will, after reflection pass through the Focal Point. Ray 2 - A ray initially directed toward the pole of the mirror, will, after reflection, leave the mirror such that angle i = angle r Ray 3 - A ray, initially directed through the Focal Point, will, after reflection, leave the mirror parallel to the Principal Axis. Generally, only two of the three “standard” rays ever need to be used to locate the position of an image. 5.5 Images - Concave Mirrors Image type, size and orientation for concave mirrors may be found by using the ray tracing technique. Concave Mirror Object The Image produced is: •REAL •INVERTED •SMALLER than the Object f Image Concave Mirror Object When the object is placed 2f from the mirror, the image is: •REAL •INVERTED •SAME SIZE as the object f Image Concave Mirror When the object is put “inside” the focal length, the image is: •VIRTUAL •UPRIGHT •LARGER than the Object Object f Image 5.6 Lens Types There are two basic types of lenses: 1. CONVEX LENS (Converging Lens). These lenses cause incoming parallel rays to be refracted to a single point. Convex Lens f 2. f CONCAVE LENS. (Diverging Lens). These lenses cause incoming parallel rays to diverge as if they originated from a focal point. Concave lens f f 5.7 Lenses - Properties & Definitions Before proceeding with image determination, a number of terms associated with lenses need to be defined. C Convex Lens R A f PA f O F F A = Aperture of Mirror (diameter of refracting surface) O = Optical Centre of the lens (the very centre of the lens) C = Centre of Curvature (centre of the sphere of which the lens surface is a part) R = Radius of Curvature (radius of sphere of which the lens surface is a part) PA = Principal Axis (a line joining the centre of curvature and the optical centre of the lens). f = Focal Points (point at which rays, initially parallel to the principal axis, meet, after refraction). Note the lens has two focal points. F = Focal Length (distance from optical centre to focal point(s)). 5.8 Ray Tracing - Lenses In order to determine the position and type of image produced by a concave mirror, a number of “standard” light rays can be used. The three most important are illustrated below: Convex Lens Object Ray 3 Ray 1 f Ray 2 f Image Ray 1 - A ray from the top of the object, initially parallel to the principal axis, will, after refraction through the lens, pass through the focal point on the far side of the lens. Ray 2 - A ray from the top of the object will pass through the optical centre of the lens undeviated. Ray 3 - A ray from the top of the object passing through the near focal point will, after refraction, emerge from the lens parallel to the principal axis. Generally, only two of the three “standard” rays are ever needed to locate the position of the image. 5.9 Images - Convex Lenses Image type, size and orientation for convex lenses may be found by using the The Image produced ray tracing technique. is: •REAL •INVERTED •SMALLER than the Object Convex Lens Object f f Image Convex Lens Image f f When the object is put “inside” the focal length, the image is: •VIRTUAL •UPRIGHT •LARGER than the Object Object Rays projected backwards WILL meet. These diverging rays will never meet. Ray Tracing 28. What is the process of determining where the image of an object is in a curved mirror or lens called ? Ray Tracing 29. How many rays are needed to locate the image of an object in a curved mirror or lens ? 2 Chapter 6 This chapter covers the following topics: • Conceptual Modelling • Light as Particles • Theories for Light 6.0 Conceptual Modelling When we observe strange or unusual behaviour in people, we often try to explain what we see by supposing the person is suffering some mental problem. They may have suffered a skull fracture resulting in brain damage, have a congenital brain defect, or have problems due to parental abuse in childhood. “Conceptual modelling” here refers to the activity of constructing abstract models of knowledge about the world of light In attempting to find a explanation for what we see, we “model” various “concepts”, in other words, we try to find or develop a theory which will fit all the behaviours we observe. We have two possible “models” available to fit light’s observed behaviours. (a) Light is a wave and all its properties and behaviours can be explained by assuming light is a wave. (b) Light is a particle and all its properties and behaviours can be explained by assuming light is a particle. 6.1 Light as Waves By assuming light is a wave all the properties and behaviours we have so far investigated can be explained by using the known properties and behaviours that waves, in general, exhibit. For example, waves undergo reflection and follow the laws of reflection exactly Waves refract according to Snell’s Law Refraction Reflection Waves produce interference patterns. Interference 6.2 Light as Particles Just as waves can be reflected, so too can particles. They also follow the laws of reflection. Particles can also undergo refraction obeying Snell’s Law. (although speed predictions are incorrect) Incident Light However, one property of light cannot be explained by the “wave model”. In the Photoelectric Effect certain metals eject electrons when illuminated by particular colours of light Ejected Electron Metal 6.3 Comparing Models Does our new found knowledge mean that the “wave model” for light is now to be replaced by the “particle model” ? Well, no because the particle model has the same limitations as the wave model, that is, it cannot adequately explain ALL known properties of light. So how useful is each theory in explaining light properties ? The table summarises. Light Property Particle Theory Wave Theory Pressure Yes Yes Reflection Yes Yes Refraction Partially Yes Diffraction No Yes Interference No Yes Yes No Photoelectric Effect 6.4 Where to Now ? This leaves us in the position of not having one single model that can describe all light’s known behaviours. So we have developed a hybrid model called the “Wave – Particle Duality”, where light is assumed to be made up of a stream of individual particles called “PHOTONS”. Photons are neither waves nor particles, having properties similar to particles when travelling through a vacuum and when in a gravitational field, while also having properties similar to waves when refracting and interfering. Photons can be pictured as a series of individual particles each of which displays some wave like properties. Individual Photon Models for Light 30. What are the two theories which compete to explain light’s behaviour ? The Wave Model and The Particle Model 31. For which particular light behaviour is the particle model inadequate ? Refraction 32. For which particular light behaviour is the wave model inadequate ? Photoelectric Effect 33. What is a Photon ? A Photon is an attempt to explain light’s behaviour with a model that has both particle and wave nature 34. What is the wave particle duality ? The wave particle duality is the currently accepted model for the explanation of light’s behaviour. Ollie Leitl 2003