* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Fig. 36-6
Nonlinear optics wikipedia , lookup
Magnetic circular dichroism wikipedia , lookup
Retroreflector wikipedia , lookup
Dispersion staining wikipedia , lookup
Anti-reflective coating wikipedia , lookup
Harold Hopkins (physicist) wikipedia , lookup
Atmospheric optics wikipedia , lookup
Nonimaging optics wikipedia , lookup
Optical aberration wikipedia , lookup
Astronomical spectroscopy wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Reflection high-energy electron diffraction wikipedia , lookup
Ultraviolet–visible spectroscopy wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Diffraction topography wikipedia , lookup
Interferometry wikipedia , lookup
Phase-contrast X-ray imaging wikipedia , lookup
Low-energy electron diffraction wikipedia , lookup
Powder diffraction wikipedia , lookup
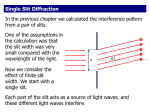
Chapter 36 Diffraction In Chapter 35, we saw how light beams passing through different slits can interfere with each other and how a beam after passing through a single slit flares—diffracts—in Young's experiment. Diffraction through a single slit or past either a narrow obstacle or an edge produces rich interference patterns. The physics of diffraction plays an important role in many scientific and engineering fields. In this chapter we explain diffraction using the wave nature of light and discuss several applications of diffraction in science and technology. (36-1) 36.2 Diffraction and the Wave Theory of Light Diffraction pattern from a single narrow slit. Side or secondary maxima Light Central maximum These patterns cannot be explained using geometrical optics (Ch. 34)! Fresnel Bright Spot. Light Bright spot (36-2) 36.3 Diffraction by a Single Slit: Locating the Minima When the path length difference between rays r1 and r2 is l/2, the two rays will be out of phase when they reach P1 on the screen, resulting in destructive interference at P1. The path length difference is the distance from the starting point of r2 at the center of the slit to point b. For D>>a, the path length difference between rays r1 and r2 is (a/2) sin q. Fig. 36-4 (36-3) Diffraction by a Single Slit: Locating the Minima, cont'd Repeat previous analysis for pairs of rays, each separated by a vertical distance of a/2 at the slit. Setting path length difference to l/2 for each pair of rays, we obtain the first dark fringes at: a l sin q a sin q l 2 2 (first minimum) For second minimum, divide slit into 4 zones of equal widths a/4 (separation between pairs of rays). Destructive interference occurs when the path length difference for each pair is l/2. a l sin q a sin q 2l (second minimum) 4 2 Dividing the slit into increasingly larger even numbers of zones, we can find higher order minima: a sin q ml , for m 1, 2,3 Fig. 36-5 (minima-dark fringes) (36-4) 36.4 Intensity in Single-Slit Diffraction, Qualitatively To obtain the locations of the minima, the slit was equally divided into N zones, each with width Dx. Each zone acts as a source of Huygens wavelets. Now these zones can be superimposed at the screen to obtain the intensity as a function of q, the angle to the central axis. To find the net electric field Eq (intensity a Eq2) at point P on the screen, we need the phase relationships among the wavelets arriving from different zones: phase 2 difference l path length difference 2 D Dx sin q l N=18 1st side max. q=0 1st min. q small Fig. 36-6 (36-5) 36.5 Intensity in Single-Slit Diffraction, Quantitatively Here we will show that the intensity at the screen due to a single slit is: sin a I q I m (36-5) a 1 a where a sin q (36-6) 2 l 2 In Eq. 36-5, minima occur when: a m , for m 1, 2,3 If we put this into Eq. 36-6 we find: Fig. 36-7 a m sin q , for m 1, 2,3 l or a sin q ml , for m 1, 2,3 (minima-dark fringes) (36-6) Proof of Eqs. 36-5 and 36-6 If we divide the slit into infinitesimally wide zones Dx, the arc of the phasors approaches the arc of a circle. The length of the arc is Em. is the difference in phase between the infinitesimal vectors at the left and right ends of the arc. is also the angle between the 2 radii marked R. Eq . The dashed line bisecting f forms two triangles, where: sin 2R Em . In radian measure: R Em 1 sin Solving the previous 2 equations for Eq one obtains: Eq 2 . 1 1 2 2 The intensity at the screen is therefore: I q Eq2 sin a 2 I q I m Im Em a 2 is related to the path length difference across the entire slit: Fig. 36-8 2 a sin q l (36-7) 36.6 Diffraction by a Circular Aperture Distant point source, e,g., star d lens sin q 1.22 l d q (1st min.- circ. aperture) Image is not a point, as expected from geometrical optics! Diffraction is responsible for this image pattern. a Light Light sin q q l a (1st min.- single slit) a q (36-8) Resolvability Rayleigh’s Criterion: Two point sources are barely resolvable if their angular separation qR results in the central maximum of the diffraction pattern of one source’s image centered on the first minimum of the diffraction pattern of the other source’s image. Fig. 36-10 q R small l l 1 q R sin 1.22 1.22 d d (Rayleigh's criterion) (36-9) 36.7 Diffraction by a Double Slit In the double-slit experiment described in Ch. 35 we assumed that the slit width a<<l. What if this is not the case? Two vanishingly narrow slits a<<l Single slit a~l Fig. 36-14 Two Single slits a~l sin a I q I m cos a 2 2 (double slit) d sin q l a a sin q l (36-10) 36.8 Diffraction Gratings A device with N slits (rulings) can be used to manipulate light, such as separate different wavelengths of light that are contained in a single beam. How does a diffraction grating affect monochromatic light? Fig. 36-17 d sin q ml for m 0,1, 2 Fig. 36-18 (maxima-lines) (36-11) Width of Lines The ability of the diffraction grating to resolve (separate) different wavelengths depends on the width of the lines (maxima). Fig. 36-20 Fig. 36-19 (36-12) Width of Lines, cont’d Nd sin Dqhw l , Dq hw Fig. 36-21 Dq hw l Nd cosq l Nd sin Dqhw Dqhw (half width of central line) (half width of line at q ) (36-13) Grating Spectroscope Separates different wavelengths (colors) of light into distinct diffraction lines Fig. 36-23 Fig. 36-22 (36-14) Optically Variable Graphics Gratings embedded in the device send out hundreds or even thousands of diffraction orders to produce virtual images that vary with the viewing angle. This is complicated to design and extremely difficult to counterfeit, so it makes an excellent security graphic. Fig. 36-25 (36-15) 36.9 Gratings: Dispersion and Resolving Power Dispersion: the angular spreading of different wavelengths by a grating Dq D (dispersion defined) Dl m D (dispersion of a grating) (36-30) d cos q Resolving Power lavg R Dl (resolving power defined) R Nm (resolving power of a grating) (36-32) (36-16) Proof of Eq. 36-30 Angular position of maxima Differential of first equation (what change in angle does a change in wavelength produce?) For small angles d sin q ml d cosq dq md l dq Dq and dl Dl d cos q Dq mDl Dq m Dl d cos q (36-17) Proof of Eq. 36-32 l Rayleigh's criterion for half width to resolve two lines Dq hw Substituting for Dq in calculation on previous slide Dq hw Dq l N Nd cos q mDl l R Nm Dl (36-18) Dispersion and Resolving Power Compared Table 36-1 Grating N d (nm) q D (o/mm) R A 10 000 2540 13.4o 23.2 10 000 B 20 000 2540 13.4o 23.2 20 000 C 10 000 1360 25.5o 46.3 10 000 Data are for l = 589 nm and m = 1 Fig. 36-26 (36-19) 36.10 X-Ray Diffraction X-rays are electromagnetic radiation with wavelength ~1 Å = 10-10 m (visible light ~5.5x10-7 m). X-ray generation X-ray wavelengths too short to be resolved by a standard optical grating Fig. 36-27 ml 1 1 0.1 nm q sin sin 0.0019 d 3000 nm 1 (36-20) X-Ray Diffraction, cont’d Diffraction of x-rays by crystal: spacing d of adjacent crystal planes on the order of 0.1 nm → three-dimensional diffraction grating with diffraction maxima along angles where reflections from different planes interfere constructively 2d sin q ml for m 0,1, 2 Fig. 36-28 (Bragg's law) (36-21) X-Ray Diffraction, cont’d Interplanar spacing d is related to the unit cell dimension a0: 5d Fig. 36-29 5 4 2 0 a a0 or d 0.2236a0 20 Not only can crystals be used to separate different x-ray wavelengths, but x-rays in turn can be used to study crystals, for example, to determine the type of crystal ordering and a0. (36-22)























![Scalar Diffraction Theory and Basic Fourier Optics [Hecht 10.2.410.2.6, 10.2.8, 11.211.3 or Fowles Ch. 5]](http://s1.studyres.com/store/data/008906603_1-55857b6efe7c28604e1ff5a68faa71b2-150x150.png)