* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download ppt
Magnetic circular dichroism wikipedia , lookup
Retroreflector wikipedia , lookup
Fourier optics wikipedia , lookup
Birefringence wikipedia , lookup
Optical aberration wikipedia , lookup
Thomas Young (scientist) wikipedia , lookup
Nonimaging optics wikipedia , lookup
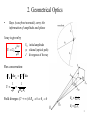
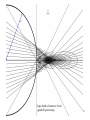
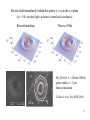
Focusing of Light in Axially Symmetric Systems within the Wave Optics Approximation Johannes Kofler Institute for Applied Physics Johannes Kepler University Linz Diploma Examination November 18th, 2004 1. Motivation • Goal: Intensity distribution behind a focusing sphere - as analytical as possible fast to compute improve physical understanding interpret and predict experimental results • Wave field behind a focusing system is hard to calculate - geometrical optics intensity: in the focal regions - diffraction wave integrals: finite but hard to calculate (integrands highly oscillatory) - available standard optics solutions (ideal lens, weak aberration): inapplicable - theory of Mie: complicated and un-instructive (only spheres) 2 2. Geometrical Optics • Rays (wavefront normals) carry the information of amplitude and phase A ray is given by ei k U U0 J U0 initial amplitude eikonal (optical path) J divergence of the ray Flux conservation: 2 2 U 0 da0 U da 1 1 U J Rm Rs Field diverges (U ) if Rm 0 or Rs 0 Rm QmAm Rs QsAs 3 Caustics • Caustics (Greek: ‘burning’): Regions where the field of geometrical optics diverges (i.e. where at least one radius of curvature is zero and the density of rays is infinitely high). 4 3. Diffraction Integrals Wave field in a point P behind a screen A: Summing up contributions from all virtual point sources on the screen (with corresponding phases and amplitudes). Scalar Helmholtz equation: ( 2 k 2 ) U (x) 0 Fresnel-Kirchhoff or Rayleigh-Sommerfeld diffraction integrals: ik U ( P) 2π A ei k s U ( A) dA s 5 For a spherically aberrated wave with small angles everywhere we get U(,z) I(R,Z) where R , Z z We introduce the integral I(R,Z) and name it Bessoid integral I ( R, Z ) J 0 ( R ρ1 ρ2 ρ4 i Z 1 1 )e 2 4 ρ1 dρ1 0 6 The Bessoid integral Bessoid Integral I 3-d: R,,Z Cuspoid catastrophe + ‘hot line’ 7 Stationary phase and geometrical optics rays 8 4. Wave Picture: Matching Geometrical Optics and Bessoid Integral Summary and Outlook: • • • • Wave optics are hard to calculate Geometrical optics solution can be “easily” calculated in many cases Paraxial case of a spherically aberrated wave Bessoid integral I(R,Z) I(R,Z) has the correct cuspoid topology of any axially symmetric 3-ray problem • Describe arbitrary non-paraxial focusing by matching the geometrical solution with the Bessoid (and its derivatives) where geometrical optics works (uniform caustic asymptotics, Kravtsov-Orlov: “Caustics, Catastrophes and Wave Fields”) 9 U geometrical ( , z ) U Bessoid ( R, Z ) 3 U0 j 1 e i k j ( , z ) J j ( , z) [ A I ( R, Z ) AR I R ( R, Z ) AZ I Z ( R, Z )] ei ( R,Z ) 6 knowns: 1, 2, 3, J1, J2, J3 6 unknowns: R, Z, , A, AR, AZ And this yields R = R(j) = R(, z) Z = Z(j) = Z(, z) = (j) = (, z) A = A(j, Jj) = A(, z) AR = AR(j, Jj) = AR(, z) AZ = AZ(j, Jj) = AZ(, z) Coordinate transformation Amplitude matching Matching removes divergences of geometrical optics Expressions on the axis rather simple 10 5. The Sphere Sphere radius: a = 3.1 µm Geometrical optics solution: f Wavelength: = 0.248 µm Refractive index: n = 1.42 a n 5.24 µm 2 n 1 Bessoid matching: f d f 1 3 π n (3 n) 1 3.93 µm 4 k a n (n 1) 11 a large depth of a narrow ‘focus’ (good for processing) 12 Illustration Bessoid-matched Bessoid integral solution Geometrical optics solution 13 Refractive index: n = 1.5 Bessoid calculation Mie theory intensity |E|2 k a a / q k a = 300 a0.248 µm 11.8 µm q k a = 100 a0.248 µm 3.9 µm q k a = 30 a0.248 µm 1.18 µm q k a = 10 a0.248 µm 0.39 µm 14 Electric field immediately behind the sphere (z a) in the x,y-plane (k a = 100, incident light x-polarized, normalized coordinates) Bessoid matching Theory of Mie SiO2/Ni-foil, = 248 nm (500 fs) sphere radius a = 3 µm linear polarization D. Bäuerle et al., Proc SPIE (2003) 15 Conclusions • • • • • • • Axially symmetric focusing leads to a generalized standard integral (Bessoid integral) with cuspoid and focal line caustic Every geometrical optics problem with axial symmetry and strong spherical aberration (cuspoid topology) can be matched with a Bessoid wave field Divergences of geometrical optics are removed thereby Simple expressions on the axis (analytical and fast) Generalization to non axially symmetric (vectorial) amplitudes via higher-order Bessoid integrals For spheres: Good agreement with the Mie theory down to Mie parameters q 20 (a/ 3) Cuspoid focusing is important in many fields of physics: - scattering theory of atoms chemical reactions propagation of acoustic, electromagnetic and water waves semiclassical quantum mechanics 16 Acknowledgements • Prof. Dieter Bäuerle • Dr. Nikita Arnold • Dr. Klaus Piglmayer, Dr. Lars Landström, DI Richard Denk, Johannes Klimstein and Gregor Langer • Prof. B. Luk’yanchuk, Dr. Z. B. Wang (DSI Singapore) 17 Appendix 18 Analytical expressions for the Bessoid integral On the axis (Fresnel sine and cosine functions): π I ( R 0,Z ) 2 Z 2 π i e 4 Z iπ erfc e 4 2 Near the axis (Bessel beam) I ( R,Z ) J 0 ( R Z ) I (0 ,Z ) 19 Numerical Computation of the Bessoid integral 1. Direct numerical integration along the real axis Integrand is highly oscillatory, integration is slow and has to be aborted T100x100 > 1 hour 2. Numerical integration along a line in the complex plane (Cauchy theorem) Integration converges T100x100 20 minutes 3. Solving numerically the corresponding differential equation for the Bessoid integral I (T100100 2 seconds !) 2i IZ ΔRI 0 (Δ R I ) R Z I R i R I 0 paraxial Helmholtz equation in polar coordinates + some tricks one ordinary differential equation in R for I (Z as parameter) 20 Properties of Bessoid important for applications: • • • • near the axis: Bessel beam with slowly varying cross section smallest width is not in the focus 3 width from axis to first zero of Bessel function: w0 8 sin (width is smaller than with any lens) diverges slowly: large depth of focus (good for processing) 21 Generalization to Vector Fields Consider (e.g.) linear polarization of incident light: Modulation of the initial (vectorial) amplitude on the spherically aberrated wavefront axial symmetry is broken Generalization to the higher-order Bessoid integrals: Im ρ1m1 J m ( R ρ2 ρ4 i Z 1 1 ρ1 ) e 2 4 dρ1 I0 I 0 Geometrical optics terms with -dependence cos(m) or sin(m) have to be matched with m-th order Bessoid integral Im Coordinate equations (R, Z, ) remain the same (cuspoid catastrophe) Amplitude equations (Am, ARm, AZm) are modified systematically 22