Download Powerpoint Slides

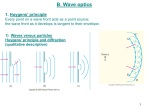
Lab 10: Wave optics
Only 2 more labs to go!!
Light is an electromagnetic wave. Because of the wave nature of light it interacts differently
than you might expect. Consider the following situation:
light rays
double slits
screen
Wave front
from light
light
source
double slits
screen
D
d

R2
intensity
maxima
The maximas in intensity occur when
the difference in path (from the two
slits) is equal to an integral number
of wavelengths. In other words, when:
central
maxima
R  n
y
R1
double slits
screen
It can be shown from trigonometry
that,
R  d sin 
So then we will have points of maximums
when:
d sin   n
Where d, is the slit separation,  is the angle between the maxima and the optical axis, n is the
order of intensity (i.e. n = 1, 2 3, ..etc.), and  is the wavelength of light.
Notice that for small angles,  < 5o, sin  = tan , and for this situation tan  is:
y
tan  
D
where, y is the distance the maxima is from the central maxima, and D is the
distance between the screen and the grating.
d sin   n
So our equation becomes:
Dn 
y
d    n  y 
d
D
Today, you are going to measure the distance spots occur from the central maxima. From
this you will be ask to calculate the slit separation and the wavelength. Let’s look at this
example:
White light is incident upon a regular array of slits. An interference pattern is observed on
a screen, a distance of 8 meters from the slits. It is noted that the second order yellow ( = 550 nm)
is at a horizontal distance of 10 cm from the center.
What will be the location of the first order yellow?

Dn 8m 1 550 10 9 m
y

d
d

Unfortunately, we don’t have the slit separation
so we need to solve for d, first.
Remember that the second order spot is found 10cm away from the center, so we can use this
information to calculate d:


Dn 8m2 550 109 m
d

 8.8 105 m
y
0.1m
Using this we can solve for y and we get:
y = 0.05 m