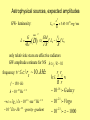Download Current results of data analysis on big interferometers

Прецизионные измерения гравитационных возмущений
оптическими интерферометрами с большой базой
В.Н.Руденко
(ГАИШ МГУ, Москва)
«Прецизионная физика и фундаментальные физические константы»
ИТФ им.А.Ф.Иоффе, С.Петербург, 6-10 дек.2010 г.
Contents
1.Introduction
2.Setup construction
3.Objectives for observation
4.Recent results
5.Cold damping spring.
6.Advanced instrument at SQL
Global network of Detectors
Coherent Analysis: why?
-Sensitivity increase
GEO 600
VIRGO
Nautilus
Auriga
Explorer
-Source direction
determination from time of
flight differences
-Polarizations measurement
-Test of GW Theory and
GW Physical properties
Astrophysical targets
- Far Universe expansion
rate Measurement
-GW energy density in the
Universe
-Knowledge of Universe at
times close to Planck’s time
Ligo interferometrs
Hanford 4km+2km
1915 Theory of G.R.
1916 Einstein predicts
gravitational waves (g.w.)
1960 Weber operates the first
detector
1970 Construction of cryogenic
detectors
begins
1984 Taylor and Hulse find the
first indirect evidence of g.w.
(Nobel Prize 1993)
2003 First light in the large
interferometer
2005-2009 First meaninful results
(upper limits)
2015 Start upgraded machines
first
Gravitational Waves (GW)
Gravitational waves give fundamental informations on the
Universe.
The four fundamental interactions coupling constants are:
Strong
s=1
E.M.
e2=1/137
Weak
GFM2=10-5
Gravitational
GM2=10-39
Some consequences of G smallness:
1)In stellar collapses Neutrinos undergo ~103interactions
before leaving the collapsing star, GW<<1.
2)After Big-Bang , electromagnetic waves decouple from
hot matter after 13000 years, neutrinos after 1s, GW
only after Planck’s Time (10-43s) .
3) It is extremely difficult to detect them.
Detection of GW
Let’s consider two freely falling particles A and B, their separation
ξα=(xA-xB)α satisfies the geodesic deviation equation:
d  1 TT 
 h 
2
2
d
2
Riemann Force
1 TT 
F  Mh  
2
XA
ξα
XB
Consequently the receiver is a device measuring spacetime curvature i.e. the relative acceleration of two
freely falling masses or their relative displacement.
Effect of Riemann Force
L
L ~ h 1022
L L
Effect of 2 Polarizations
h+
hx
INTERFEROMETRIC DETECTORS
Large L
High sensitivity
Very Large Bandwidth 10-10000 Hz
Mirrors
Beam Splitter
LA
LB
Signal
L =LA-LB
Laser
Displacement sensitivity can reach ~10-19-10-20 m, then, for
measuring L/L~10-22 LA and LB should be km long.
Astrophysical sources, expected amplitudes
c5
L0 
 3.63 1059 erg / sec
G
GW- luminosity:

2
rg 5
G
GM 5
L
 ( 5 ) L0 ~ ( ) L0
5 ( D)
45c
c R
R
only relativistic stars are effective radiators
GW amplitude estimate for NS h  rg / R ~ 0.1
frequency: 
 c / rg ~ 10..kHz
h ~ 10  22 Hz 1 / 2
   g x / x ~ 10

R r
~ 10 18  Galaxy
f ~ 150  Hz
16
h
rg rg
2
 sec Hz
1/ 2
~ 107 Etv  Hz 1/ 2  gravity  gradient
~ 10 21  Virgo
~ 10 23  z ~ 1000
GW DETECTORS SENSITIVITY
TAMA 300
GEO600
AURIGA,
NAUTILUS,
EXPLORER
Virgo
LIGO
Frequency Range:
(50 – 1500) Hz
Blind All Sky Searching
Sources:
- compact binary systems evolution
(inspiral, merging, ring down)
- supernova collapse events
- continuous GW radiation (Pulsars)
- stochastic GW background
- Triggered Search ( Astro-gravity associations)
Bursts
• Classical sources: supernovae
– Waveform poorly known
– Several events/year in the Virgo cluster
• Possibly detectable only within our Galaxy
•
Generally, whatever can cause short ( < 1s ) GW impulses
– Include exotic things (strings) or classical things (NS, BH ringdowns)
GW emitted
15
Coalescing Binaries
• Source: coalescence of compact binary
stars (BNS, BBH, NS/BH)
– Waveform accurately modeled in the first and last phase
• Allows matched filtering
– Less known in the “merger” phase
• Interesting physics here, for instance for BNS
– Rate very uncertain
• A few events/year could be accessible to the LSC-Virgo network
chirp
16
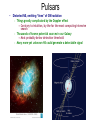
Pulsars
•
Distorted NS, emitting “lines” of GW radiation
– Things greatly complicated by the Doppler effect
• Contrary to intuition, by the far the most computing intensive
search
– Thousands of known potential sources in our Galaxy
• Most probably below detection threshold
– Many more yet unknown NS could generate a detectable signal
17
Cosmological Stochastic Background
• Potential access to very early Universe
CMBR
Relic
gravitons
Relic neutrinos
18
LIGO Scientific Runs
(2000 – 2007)
S1 – (08-09) 2000 y. ( noise 100 times projected level)
S2 , S3 - during 2003 y (bad seismic isolation)
S4 - (02-03) 2005 y ( duty cycle 70%, but selected 15,5
days data !)
joint operation of 3 interferometers
S5 - (06. 2006 - 10.2007)
main results
Basic searching algorithms
Non modeled Bursts
outputs of two GW detectors:
total energy : E =
vectors a , b
2
2
2


a

b
a

b
2
a
b




normalized and integrated at the
Burst’s Excess Power:
it is reduced to variables:

(b
) ,
E

(a
) , E
b~
i /
a~
i /
2
2
i
i
E  Cthr
Burst’s Cross Power:




1
/
2
R

(
E

E
/
)
~

a

b
/a
b
ab a
b 
R  R0
S.Klimenko, GWDAW14, January 26, 2010, Rome, LIGO-G1000033-v8
Results of the all-sky search for gravitational wave burst signals are presented for the first
joint LIGO (S5) and Virgo VSR1 runs in 2006-2007.
The analysis has been performed with three different search algorithms in a wide
frequency band between 50-6000 Hz.
No plausible GW candidates have been identified.
As a result, a limit on the rate of burst GW signals (combined with the LIGO
results from the first S5 year) has been established:
less than 2 events per year at 90% confidence level
with sensitivity in the range 6-20 × 10−22 Hz−1/2
This rate limit is increased by more than an order of magnitude compared to the previous
LIGO runs.
What we known about SBGW from BBN bound ?
gw=(1/c)dgw/dlog(f)
h0 gw , h0=0.73(3)
gw =  d log(f) [dgw/dlog(f)]
• from the balance of H and Γ at nucleosynthesis, (H2 =(8πG/3) ρ)
• is a bound on the total energy density, integrated over all frequencies.
fmin ≈10-10 Hz fixed by the horizon size at BBN
• Nν = effective number of neutrino species, parametrizes any extra energy contribution
• in the SM, Nν ~ (4.4 – 3.046)
(due to residual interaction ν with e± QED effects).
•So in order of magnitude at time of NS there were no more GWs than photons
• it can be translated into a bound on the integrand
f


6
h

(
f
)

d
(log
f
)



5
.
6

10

(
N

3
)

0gw
f
min
gw < 6.9 10-6
Results S4 , S5 ,
Unmodeled bursts :
[last run S6 (04.09 – 09.10)]
upper limit → < 0.15 day -1 , h rss < 10-20 Hz – ½
Inspiral Bursts :
upper limit → Event Rate: R
R = (Number of events/ year. galaxy)
1 event per 20-300 years for NS binary
for dH ~ 60 Mpc
1 event per 20-2000 years for binary ~ 5 M0
1 event per 3 – 30 years for binary ~ 10 M0
Pulsars : f ~ 150 Hz ,
Stochastic background:
h ~ 10-25 , ε < 10-5
f ~(50 – 100) Hz,
Ω < 6.5 10^{-5}
Существенные результаты LIGO
1. Новый (значимый) верхний предел на ГВ-сигнал от гамма-всплесков.
Во время серии S5 имело место событие: GRB 070201 – короткий г-всплеск (< 2 сек),
положение источника отождествлено с М31 (~770 кпс) (reg. Integral, Messenger, Swift)
fl.~10^{-5}erg/cm^{2}. В окне 180 сек. вокруг tarv искали сопровождающий ГВ-импульс.
С вероятностью ~95% ГВ сигнал не обнаружен. Предел на его интенсивность в модели
NS, BH – “binary coalescence” оценен как E < 4.4 10^{-4} M0c2 (1M0<m1<3M0 , 3M0<m2<40M0)
f~150 Hz (теор. pасчет для ВС NS допускает E ~10^{-2} !)
2. Перекрытие «предела замедления» на ГВ излучение пульсаров
PSR BO531+21, PSR JO534-22, Crab Neb. (ν~30 Hz, dν/dt~-3 10^{-10} Hz/s )
Теор. оценка по “spin-down rate” даёт hgw ~ 1.4 10^{-24}. Наблюдения S5, 3 мес.(~200 дн.)
на частоте ν ~ 60 Hz дали hgw<3.4 10^{-25} или для степени несферичности: ε < 1.8 10^{-4}
3. Перекрытие предела стохастического ГВ-фона по нуклеоситезу в
ранней Вселенной
теория нуклеосинтеза дает ограничение на интегральную (по частоте) плотность ГВ фона
из предположения, что гравитонов было не больше, чем фотонов; это даёт при равномерной
спектральной плотности ГВ фона gw ~ 9.7 10^{-6}. Экспериментально за время наблюдения
~200 дней на детекторах H1, L1 получена оценка gw ~ 6.9 10^{-6} с достоверностью 95%
Cold Spring Damping of Thermal Noise
in the LIGO setup
New Journal of Physics 11 (2009) 073032, B Abbott1 et.al. (LSC)
Observation of quantum effects such as ground state cooling,
quantum jumps, optical squeezing, and entanglement that involve
macroscopic mechanical systems are the subject of intense
experimental effort.
The first step toward engineering a non-classical state of a
mechanical oscillator is to cool it, minimizing the thermal occupation
number of the mode. Any mechanical coupling to the environment
admits thermal noise that randomly drives the system’s motion, as
dictated by the fluctuation–dissipation theorem, but ‘cold’ frictionless
forces, such as optical or electronic feedback, can suppress this
motion, hence cooling the oscillator.
Thermal standard:
x 
kT
(   r )
2
m
x 
kT 
m 2 Q
 r
T0 , Q  , (H0)
Quantum standard:
xSQL 
LIGO displacement sensitivity:
S5 scientific run
h
~ 5.10 18 cm
m
m  10..kg,...  2 .150.rad / sec
~ 2.10 16 cm
f  150.Hz.. ~ 102 sec .
Quantum behaviour of macroscopic test body (?)
V.B.Braginskii. Physics Uspekhi, v.48, 595, 2005
a pendulum in gravity field, mode of acoustical resonator etc. can
demonstrate quantum features under the following requirement:
E  kT
2
r
 kT

Q
 
instead of usual condition
kT  
Dodonov V.V., Manko V.I., Rudenko V.N., Quantum Electronics, v.7 (№10), p.2124, 1980
«Quantum properties of macroscopic resonator with a high quality factor»
-a) classical calculation mean values and a system evolution corresponds to quantum
calculation with the accuracy ~ O(1/n)
-b) transition probability requires only the quantum calculation;
-c) observation of «energy steps» requires unrealistic measurement accuracy (Q ~ 1018 )
Realistic objective is a preparation of macroscopic system (oscillator) in the
ground energetic state, i.e. with n ~ 1.
«procedure of super cooling»
in expectation of
«macroscopic quantum effects»
n
kT

LIGO’s Hanford Observatory. The detector shown comprises a
Michelson interferometer with a 4 km long Fabry–Perot cavity of finesse 220
placed in each arm to increase the sensitivity of the detector. Each mirror of
the interferometer has mass M = 10.8 kg, and is suspended from a vibrationisolated platform on a fine wire to form a pendulum with frequency 0.74 Hz,
to shield it from external forces
To minimize the effects of laser shot noise, the interferometer operates with
high power levels; approximately 400W of laser power of wavelength 1064
nm is incident on the beam splitter, resulting in over 15kW of laser power
circulating in each arm cavity. The present detectors are sensitive to
changes in relative mirror displacements of about 10−18 m in a 100 Hz
band centered around 150 Hz (figure 2).
Differential arm cavity motion, which is the degree of freedom excited by a
passing gravitational wave, and hence also the most sensitive to mirror
displacements. This mode corresponds to the differential motion of the
centers of mass of the four mirrors, xc = (x1 −x2)−(x3 −x4), and has a
reduced mass of Mr = 2.7 kg.
GW- интерферометр как «квадрупольный осциллятор,
управляемый холодной электронно-оптической жесткостью
(пружиной)»
координата ц.масс
ХC = (Х2 – Х1) – (Х3 – Х4) ,
приведенная масса Мr ~ 2.7 kg
наблюдаемый сигнал ХS = XC – XN (тепловой шум зеркала + шум импульса фотонов)
динамика
 M r [ 2  j p (1 / Q)   p 
2
K ()
  2 eff  jeff
Mr
эл.-опт. пружина
K ( )
] X c  FN  K () X N
Mr
eff , eff   p , p
 M r [2  jeff  2eff ] X c  FN  K () X N
при
K () X N  FN
осциллятор управляется электронно-оптической жесткостью
K ( )
FN  0,... X C 
XS
2
M r
Teff
M r 2 eff X 2 rms

kB
Результаты измерений на интерферометре Н1
Neff 
kTeff
eff
eff  140  Гц
Teff  1.4  0.2  K
N eff  234  35
Advanced LIGO (2015) – планирует снижение эффективного шумового
уровня в 20 – 30 раз. Это позволит вплотную приблизиться к
реализации макроскопического осциллятора с флуктуациями энергии
вблизи низшего энергетического состояния, т.е. эффективность
искусственного охлаждения достигнет квантового предела.
Классические измерительные методы перестанут работать,
потребуется практическое развитие методов т.н.«квантовых не
возмущающих измерений».
GW-experiment: News
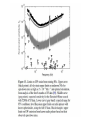
Fig. 1. Advanced Virgo sensitivity curve compared with Virgo
and LIGO design and current bar sensitivity. Violin modes are
not displayed for clarity