* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Wilcoxon sum
Survey
Document related concepts
Transcript
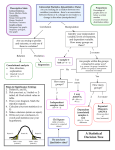
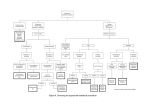
Introduction to choosing the correct statistical test + Tests for Continuous Outcomes I Questions to ask yourself: 1. 2. 3. What is the outcome (dependent) variable? Is the outcome variable continuous, binary/categorical, or timeto-event? What is the unit of observation? 4. person* (most common) lesion half a face physician clinical center Are the observations independent or correlated? Independent: observations are unrelated (usually different, unrelated people) Correlated: some observations are related to one another, for example: the same person over time (repeated measures), lesions within a person, half a face, hands within a person, controls who have each been selected to a particular case, sibling pairs, husband-wife pairs, mother-infant pairs Correlated data example Split-face trial: Researchers assigned 56 subjects to apply SPF 85 sunscreen to one side of their faces and SPF 50 to the other prior to engaging in 5 hours of outdoor sports during midday. Sides of the face were randomly assigned; subjects were blinded to SPF strength. Outcome: sunburn Russak JE et al. JAAD 2010; 62: 348-349. Results: Table I -- Dermatologist grading of sunburn after an average of 5 hours of skiing/snowboarding (P = .03; Fisher’s exact test) Sun protection factor Sunburned Not sunburned 85 1 55 50 8 48 Fisher’s exact test compares the following proportions: 1/56 versus 8/56. Note that individuals are being counted twice! Correct analysis of data… Table 1. Correct presentation of the data from: Russak JE et al. JAAD 2010; 62: 348-349. (P = .016; McNemar’s test). SPF-50 side SPF-85 side Sunburned Not sunburned Sunburned 1 0 Not sunburned 7 48 McNemar’s test evaluates the probability of the following: In all 7 out of 7 cases where the sides of the face were discordant (i.e., one side burnt and the other side did not), the SPF 50 side sustained the burn. Overview of common statistical tests Are the observations correlated? Outcome Variable Continuous (e.g. blood pressure, age, pain score) Binary or categorical (e.g. breast cancer yes/no) Time-to-event (e.g. time-to-death, time-to-fracture) independent correlated Ttest ANOVA Linear correlation Linear regression Paired ttest Repeated-measures ANOVA Mixed models/GEE modeling Outcome is normally distributed (important for small samples). Outcome and predictor have a linear relationship. Chi-square test Relative risks Logistic regression McNemar’s test Conditional logistic regression GEE modeling Chi-square test assumes sufficient numbers in each cell (>=5) Kaplan-Meier statistics Cox regression n/a Cox regression assumes proportional hazards between groups Assumptions Overview of common statistical tests Are the observations correlated? Outcome Variable Continuous (e.g. blood pressure, age, pain score) Binary or categorical (e.g. breast cancer yes/no) Time-to-event (e.g. time-to-death, time-to-fracture) independent correlated Ttest ANOVA Linear correlation Linear regression Paired ttest Repeated-measures ANOVA Mixed models/GEE modeling Outcome is normally distributed (important for small samples). Outcome and predictor have a linear relationship. Chi-square test Relative risks Logistic regression McNemar’s test Conditional logistic regression GEE modeling Sufficient numbers in each cell (>=5) Kaplan-Meier statistics Cox regression n/a Cox regression assumes proportional hazards between groups Assumptions Continuous outcome (means) Are the observations correlated? Outcome Variable Continuous (e.g. blood pressure, age, pain score) independent correlated Ttest: compares means Paired ttest: compares means between two independent groups ANOVA: compares means between more than two independent groups Pearson’s correlation coefficient (linear correlation): shows linear correlation between two continuous variables Linear regression: multivariate regression technique when the outcome is continuous; gives slopes or adjusted means between two related groups (e.g., the same subjects before and after) Repeated-measures ANOVA: compares changes over time in the means of two or more groups (repeated measurements) Mixed models/GEE modeling: multivariate regression techniques to compare changes over time between two or more groups Alternatives if the normality assumption is violated (and small n): Non-parametric statistics Wilcoxon sign-rank test: non-parametric alternative to paired ttest Wilcoxon sum-rank test (=Mann-Whitney U test): nonparametric alternative to the ttest Kruskal-Wallis test: non- parametric alternative to ANOVA Spearman rank correlation coefficient: non-parametric alternative to Pearson’s correlation coefficient Continuous outcome (means) Are the observations correlated? Outcome Variable Continuous (e.g. blood pressure, age, pain score) independent correlated Ttest: compares means Paired ttest: compares means between two independent groups ANOVA: compares means between more than two independent groups Pearson’s correlation coefficient (linear correlation): shows linear correlation between two continuous variables Linear regression: multivariate regression technique when the outcome is continuous; gives slopes or adjusted means between two related groups (e.g., the same subjects before and after) Repeated-measures ANOVA: compares changes over time in the means of two or more groups (repeated measurements) Mixed models/GEE modeling: multivariate regression techniques to compare changes over time between two or more groups Alternatives if the normality assumption is violated (and small n): Non-parametric statistics Wilcoxon sign-rank test: non-parametric alternative to paired ttest Wilcoxon sum-rank test (=Mann-Whitney U test): nonparametric alternative to the ttest Kruskal-Wallis test: non- parametric alternative to ANOVA Spearman rank correlation coefficient: non-parametric alternative to Pearson’s correlation coefficient Example: two-sample t-test In 1980, some researchers reported that “men have more mathematical ability than women” as evidenced by the 1979 SAT’s, where a sample of 30 random male adolescents had a mean score ± 1 standard deviation of 436±77 and 30 random female adolescents scored lower: 416±81 (genders were similar in educational backgrounds, socio-economic status, and age). Do you agree with the authors’ conclusions? Two sample ttest Statistical question: Is there a difference in SAT math scores between men and women? What is the outcome variable? Math SAT scores What type of variable is it? Continuous Is it normally distributed? Yes Are the observations correlated? No Are groups being compared, and if so, how many? Yes, two two-sample ttest Two-sample ttest mechanics… Data Summary Group 1: women Group 2: men n Sample Mean Sample Standard Deviation 30 416 81 30 436 77 Two-sample t-test 1. Define your hypotheses (null, alternative) H0: ♂-♀ math SAT = 0 Ha: ♂-♀ math SAT ≠ 0 [two-sided] Two-sample t-test 2. Specify your null distribution: F and M have approximately equal standard deviations/variances, so make a “pooled” estimate of standard deviation/variance: 81 77 sp 79 2 s 2p 792 The standard error of a difference of two means is: 2 2 792 792 20.4 n m 30 30 sp sp Differences in means follow a T-distribution… T distribution A t-distribution is like a Z distribution, except has slightly fatter tails to reflect the uncertainty added by estimating the standard deviation. The bigger the sample size (i.e., the bigger the sample size used to estimate ), then the closer t becomes to Z. If n>100, t approaches Z. Student’s t Distribution Note: t Z as n increases Standard Normal (t with df = ) t (df = 13) t-distributions are bellshaped and symmetric, but have ‘fatter’ tails than the normal t (df = 5) 0 from “Statistics for Managers” Using Microsoft® Excel 4th Edition, Prentice-Hall 2004 t Student’s t Table Upper Tail Area df .25 .10 .05 1 1.000 3.078 6.314 Let: n = 3 df = n - 1 = 2 = .10 /2 =.05 2 0.817 1.886 2.920 /2 = .05 3 0.765 1.638 2.353 The body of the table contains t values, not probabilities from “Statistics for Managers” Using Microsoft® Excel 4th Edition, Prentice-Hall 2004 0 2.920 t t distribution values With comparison to the Z value Confidence t Level (10 d.f.) t (20 d.f.) t (30 d.f.) Z ____ .80 1.372 1.325 1.310 1.28 .90 1.812 1.725 1.697 1.64 .95 2.228 2.086 2.042 1.96 .99 3.169 2.845 2.750 2.58 Note: t Z as n increases from “Statistics for Managers” Using Microsoft® Excel 4th Edition, Prentice-Hall 2004 Two-sample t-test 2. Specify your null distribution: F and M have approximately equal standard deviations/variances, so make a “pooled” estimate of standard deviation/variance: 81 77 sp 79 2 s 2p 792 The standard error of a difference of two means is: 2 2 792 792 20.4 n m 30 30 sp sp Differences in means follow a T-distribution; here we have a T-distribution with 58 degrees of freedom (60 observations – 2 means)… Two-sample t-test 3. Observed difference in our experiment = 20 points Two-sample t-test 4. Calculate the p-value of what you observed Critical value for two-tailed p-value of .05 for T58=2.000 0.98<2.000, so p>.05 20 0 T58 .98 20.4 p .33 5. Do not reject null! No evidence that men are better in math ;) Corresponding confidence interval… 20 2.00 * 20.4 20.8 60.8 Note that the 95% confidence interval crosses 0 (the null value). Review Question 1 A t-distribution: a. b. c. d. Is approximately a normal distribution if n>100. Can be used interchangeably with a normal distribution as long as the sample size is large enough. Reflects the uncertainty introduced when using the sample, rather than population, standard deviation. All of the above. Review Question 1 A t-distribution: a. b. c. d. Is approximately a normal distribution if n>100. Can be used interchangeably with a normal distribution as long as the sample size is large enough. Reflects the uncertainty introduced when using the sample, rather than population, standard deviation. All of the above. Review Question 2 In a medical student class, the 6 people born on odd days had heights of 64.64 inches; the 10 people born on even days had heights of 71.15 inches. Height is roughly normally distributed. Which of the following best represents the correct statistical test for these data? a. Z 71.1 64.6 6.5 1.44; p ns 4.5 4.5 b. Z 71.1 64.6 6.5 4.6; p .0001 4.5 1.4 16 c. T14 d. T14 71.1 64.6 4.7 2 4.7 2 10 6 6.5 2.7; p .05 2.4 71.1 64.6 6.5 1.44; p ns 4.5 4.5 Review Question 2 In a medical student class, the 6 people born on odd days had heights of 64.64 inches; the 10 people born on even days had heights of 71.15 inches. Height is roughly normally distributed. Which of the following best represents the correct statistical test for these data? a. Z 71.1 64.6 6.5 1.44; p ns 4.5 4.5 b. Z 71.1 64.6 6.5 4.6; p .0001 4.5 1.4 16 c. T14 d. T14 71.1 64.6 4.7 2 4.7 2 10 6 6.5 2.7; p .05 2.4 71.1 64.6 6.5 1.44; p ns 4.5 4.5 Continuous outcome (means) Are the observations correlated? Outcome Variable Continuous (e.g. blood pressure, age, pain score) independent correlated Ttest: compares means Paired ttest: compares means between two independent groups ANOVA: compares means between more than two independent groups Pearson’s correlation coefficient (linear correlation): shows linear correlation between two continuous variables Linear regression: multivariate regression technique when the outcome is continuous; gives slopes or adjusted means between two related groups (e.g., the same subjects before and after) Repeated-measures ANOVA: compares changes over time in the means of two or more groups (repeated measurements) Mixed models/GEE modeling: multivariate regression techniques to compare changes over time between two or more groups Alternatives if the normality assumption is violated (and small n): Non-parametric statistics Wilcoxon sign-rank test: non-parametric alternative to paired ttest Wilcoxon sum-rank test (=Mann-Whitney U test): nonparametric alternative to the ttest Kruskal-Wallis test: non- parametric alternative to ANOVA Spearman rank correlation coefficient: non-parametric alternative to Pearson’s correlation coefficient Example: paired ttest TABLE 1. Difference between Means of "Before" and "After" Botulinum Toxin A Treatment Before BTxnA After BTxnA Difference Significance Social skills 5.90 5.84 NS .293 Academic performance 5.86 5.78 .08 .068** Date success 5.17 5.30 .13 .014* Occupational success 6.08 5.97 .11 .013* Attractiveness 4.94 5.07 .13 .030* Financial success 5.67 5.61 NS .230 Relationship success 5.68 5.68 NS .967 Athletic success 5.15 5.38 .23 .000** * Significant at 5% level. Significant at 1% level. ** Paired ttest Statistical question: Is there a difference in date success after BoTox? What is the outcome variable? Date success What type of variable is it? Continuous Is it normally distributed? Yes Are the observations correlated? Yes, it’s the same patients before and after How many time points are being compared? Two paired ttest Paired ttest mechanics 1. 2. 3. 4. 5. 6. Calculate the change in date success score for each person. Calculate the average change in date success for the sample. (=.13) Calculate the standard error of the change in date success. (=.05) Calculate a T-statistic by dividing the mean change by the standard error (T=.13/.05=2.6). Look up the corresponding p-values. (T=2.6 corresponds to p=.014). Significant p-values indicate that the average change is significantly different than 0. Paired ttest example 2… Patient BP Before (diastolic) BP After 1 100 92 2 89 84 3 83 80 4 98 93 5 108 98 6 95 90 Example problem: paired ttest Patient Diastolic BP Before D. BP After Change 1 100 92 -8 2 89 84 -5 3 83 80 -3 4 98 93 -5 5 108 98 -10 6 95 90 -5 Null Hypothesis: Average Change = 0 Example problem: paired ttest X 8 5 3 5 10 5 36 6 6 6 Change -8 ( 8 6) 2 ( 5 6) 2 ( 3 6) 2 ... sx 5 4 1 9 1 16 1 32 2.5 5 5 -5 -3 -5 sx 2.5 1.0 6 60 T5 6 1.0 Null Hypothesis: Average Change = 0 With 5 df, T>2.571 corresponds to p<.05 (two-sided test) -10 -5 Example problem: paired ttest Change 95% CI : - 6 2.571* (1.0) (-3.43, - 8.571) Note: does not include 0. -8 -5 -3 -5 -10 -5 Continuous outcome (means) Are the observations correlated? Outcome Variable Continuous (e.g. blood pressure, age, pain score) independent correlated Ttest: compares means Paired ttest: compares means between two independent groups ANOVA: compares means between more than two independent groups Pearson’s correlation coefficient (linear correlation): shows linear correlation between two continuous variables Linear regression: multivariate regression technique when the outcome is continuous; gives slopes or adjusted means between two related groups (e.g., the same subjects before and after) Repeated-measures ANOVA: compares changes over time in the means of two or more groups (repeated measurements) Mixed models/GEE modeling: multivariate regression techniques to compare changes over time between two or more groups Alternatives if the normality assumption is violated (and small n): Non-parametric statistics Wilcoxon sign-rank test: non-parametric alternative to paired ttest Wilcoxon sum-rank test (=Mann-Whitney U test): nonparametric alternative to the ttest Kruskal-Wallis test: non- parametric alternative to ANOVA Spearman rank correlation coefficient: non-parametric alternative to Pearson’s correlation coefficient Using our class data… Hypothesis: Students who consider themselves street smart drink more alcohol than students who consider themselves book smart. Null hypothesis: no difference in alcohol drinking between street smart and book smart students. “Non-normal” class data…alcohol… Wilcoxon sum-rank test Statistical question: Is there a difference in alcohol drinking between street smart and book smart students? What is the outcome variable? Weekly alcohol intake (drinks/week) What type of variable is it? Continuous Is it normally distributed? No (and small n) Are the observations correlated? No Are groups being compared, and if so, how many? two Wilcoxon sum-rank test Results: Book smart: Mean=1.6 drinks/week; median = 1.5 Street smart: Mean=2.7 drinks/week; median = 3.0 Wilcoxon rank-sum test mechanics… Book smart values (n=13): 0 0 0 0 1 1 2 2 2 3 3 4 5 Street Smart values (n=7): 0 0 2 3 3 5 6 Combined groups (n=20): 0 0 0 0 0 0 1 1 2 2 2 2 3 3 334556 Corresponding ranks: 3.5* 3.5 3.5 3.5 3.5 3.5 7.5 7.5 10.5 10.5 10.5 10.5 14.5 14.5 14.5 14.5 17 18.5 18.5 20 *ties are assigned average ranks; e.g., there are 6 zero’s, so zero’s get the average of the ranks 1 through 6. Wilcoxon rank-sum test… Ranks, book smart: 3.5 3.5 3.5 3.5 7.5 7.5 10.5 10.5 10.5 14.5 14.5 17 18.5 Ranks, street smart: 3.5 3.5 10.5 14.5 14.5 18.5 20 Sum of ranks book smart: 3.5+3.5+3.5+3.5+7.5+7.5+10.5+10.5+10.5+ 14.5+14.5+17+18.5= 125 Sum of ranks street smart: 3.5+3.5+10.5+14.5 +14.5+18.5+20= 85 Wilcoxon sum-rank test compares these numbers accounting for the differences in sample size in the two groups. Resulting p-value (from computer) = 0.24 Not significantly different! Example 2, Wilcoxon sum-rank test… 10 dieters following Atkin’s diet vs. 10 dieters following Jenny Craig Hypothetical RESULTS: Atkin’s group loses an average of 34.5 lbs. J. Craig group loses an average of 18.5 lbs. Conclusion: Atkin’s is better? Example: non-parametric tests BUT, take a closer look at the individual data… Atkin’s, change in weight (lbs): +4, +3, 0, -3, -4, -5, -11, -14, -15, -300 J. Craig, change in weight (lbs) -8, -10, -12, -16, -18, -20, -21, -24, -26, -30 Jenny Craig 30 25 20 P e r c 15 e n t 10 5 0 -30 -25 -20 -15 -10 -5 0 5 Weight Change 10 15 20 Atkin’s 30 25 20 P e r c 15 e n t 10 5 0 -300 -280 -260 -240 -220 -200 -180 -160 -140 -120 -100 -80 Weight Change -60 -40 -20 0 20 Wilcoxon Rank-Sum test RANK the values, 1 being the least weight loss and 20 being the most weight loss. Atkin’s +4, +3, 0, -3, -4, -5, -11, -14, -15, -300 1, 2, 3, 4, 5, 6, 9, 11, 12, 20 J. Craig -8, -10, -12, -16, -18, -20, -21, -24, -26, -30 7, 8, 10, 13, 14, 15, 16, 17, 18, 19 Wilcoxon Rank-Sum test Sum of Atkin’s ranks: 1+ 2 + 3 + 4 + 5 + 6 + 9 + 11+ 12 + 20=73 Sum of Jenny Craig’s ranks: 7 + 8 +10+ 13+ 14+ 15+16+ 17+ 18+19=137 Jenny Craig clearly ranked higher! P-value *(from computer) = .018 Review Question 3 When you want to compare mean blood pressure between two groups, you should: a. b. c. d. e. Use a ttest Use a nonparametric test Use a ttest if blood pressure is normally distributed. Use a two-sample proportions test. Use a two-sample proportions test only if blood pressure is normally distributed. Review Question 3 When you want to compare mean blood pressure between two groups, you should: a. b. c. d. e. Use a ttest Use a nonparametric test Use a ttest if blood pressure is normally distributed. Use a two-sample proportions test. Use a two-sample proportions test only if blood pressure is normally distributed. Continuous outcome (means) Are the observations correlated? Outcome Variable Continuous (e.g. blood pressure, age, pain score) independent correlated Ttest: compares means Paired ttest: compares means between two independent groups ANOVA: compares means between more than two independent groups Pearson’s correlation coefficient (linear correlation): shows linear correlation between two continuous variables Linear regression: multivariate regression technique when the outcome is continuous; gives slopes or adjusted means between two related groups (e.g., the same subjects before and after) Repeated-measures ANOVA: compares changes over time in the means of two or more groups (repeated measurements) Mixed models/GEE modeling: multivariate regression techniques to compare changes over time between two or more groups Alternatives if the normality assumption is violated (and small n): Non-parametric statistics Wilcoxon sign-rank test: non-parametric alternative to paired ttest Wilcoxon sum-rank test (=Mann-Whitney U test): nonparametric alternative to the ttest Kruskal-Wallis test: non- parametric alternative to ANOVA Spearman rank correlation coefficient: non-parametric alternative to Pearson’s correlation coefficient DHA and eczema… P-values from Wilcoxon signrank tests Figure 3 from: Koch C, Dölle S, Metzger M, Rasche C, Jungclas H, Rühl R, Renz H, Worm M. Docosahexaenoic acid (DHA) supplementation in atopic eczema: a randomized, double-blind, controlled trial. Br J Dermatol. 2008 Apr;158(4):786-92. Epub 2008 Jan 30. Wilcoxon sign-rank test Statistical question: Did patients improve in SCORAD score from baseline to 8 weeks? What is the outcome variable? SCORAD What type of variable is it? Continuous Is it normally distributed? No (and small numbers) Are the observations correlated? Yes, it’s the same people before and after How many time points are being compared? two Wilcoxon sign-rank test Wilcoxon sign-rank test mechanics… 1. Calculate the change in SCORAD score for each participant. 2. Rank the absolute values of the changes in SCORAD score from smallest to largest. 3. Add up the ranks from the people who improved and, separately, the ranks from the people who got worse. 4. The Wilcoxon sign-rank compares these values to determine whether improvements significantly exceed declines (or vice versa). Continuous outcome (means) Are the observations correlated? Outcome Variable Continuous (e.g. blood pressure, age, pain score) independent correlated Ttest: compares means Paired ttest: compares means between two independent groups ANOVA: compares means between more than two independent groups Pearson’s correlation coefficient (linear correlation): shows linear correlation between two continuous variables Linear regression: multivariate regression technique when the outcome is continuous; gives slopes or adjusted means between two related groups (e.g., the same subjects before and after) Repeated-measures ANOVA: compares changes over time in the means of two or more groups (repeated measurements) Mixed models/GEE modeling: multivariate regression techniques to compare changes over time between two or more groups Alternatives if the normality assumption is violated (and small n): Non-parametric statistics Wilcoxon sign-rank test: non-parametric alternative to paired ttest Wilcoxon sum-rank test (=Mann-Whitney U test): nonparametric alternative to the ttest Kruskal-Wallis test: non- parametric alternative to ANOVA Spearman rank correlation coefficient: non-parametric alternative to Pearson’s correlation coefficient ANOVA example Mean micronutrient intake from the school lunch by school Calcium (mg) Iron (mg) Folate (μg) Zinc (mg) a Mean SDe Mean SD Mean SD Mean SD S1a, n=28 117.8 62.4 2.0 0.6 26.6 13.1 1.9 1.0 S2b, n=25 158.7 70.5 2.0 0.6 38.7 14.5 1.5 1.2 S3c, n=21 206.5 86.2 2.0 0.6 42.6 15.1 1.3 0.4 School 1 (most deprived; 40% subsidized lunches). b School 2 (medium deprived; <10% subsidized). c School 3 (least deprived; no subsidization, private school). d ANOVA; significant differences are highlighted in bold (P<0.05). P-valued 0.000 0.854 0.000 0.055 FROM: Gould R, Russell J, Barker ME. School lunch menus and 11 to 12 year old children's food choice in three secondary schools in Englandare the nutritional standards being met? Appetite. 2006 Jan;46(1):86-92. ANOVA Statistical question: Does calcium content of school lunches differ by school type (privileged, average, deprived) What is the outcome variable? Calcium What type of variable is it? Continuous Is it normally distributed? Yes Are the observations correlated? No Are groups being compared and, if so, how many? Yes, three ANOVA ANOVA (ANalysis Of VAriance) Idea: For two or more groups, test difference between means, for normally distributed variables. Just an extension of the t-test (an ANOVA with only two groups is mathematically equivalent to a t-test). One-Way Analysis of Variance Assumptions, same as ttest Normally distributed outcome Equal variances between the groups Groups are independent Hypotheses of One-Way ANOVA H 0 : μ1 μ 2 μ 3 H 1 : Not all of the population means are the same ANOVA It’s like this: If I have three groups to compare: I could do three pair-wise ttests, but this would increase my type I error So, instead I want to look at the pairwise differences “all at once.” To do this, I can recognize that variance is a statistic that let’s me look at more than one difference at a time… The “F-test” Is the difference in the means of the groups more than background noise (=variability within groups)? Summarizes the mean differences between all groups at once. Variabilit y between groups F Variabilit y within groups Analogous to pooled variance from a ttest. The F-distribution A ratio of variances follows an F-distribution: 2 between 2 within ~ Fn ,m The F-test tests the hypothesis that two variances are equal. F will be close to 1 if sample variances are equal. 2 2 H 0 : between within H a : 2 between 2 within ANOVA example 2 Randomize 33 subjects to three groups: 800 mg calcium supplement vs. 1500 mg calcium supplement vs. placebo. Compare the spine bone density of all 3 groups after 1 year. Spine bone density vs. treatment 1.2 1.1 1.0 S P I N E 0.9 Within group variability Between group variation Within group variability Within group variability 0.8 0.7 PLACEBO 800mg CALCIUM 1500 mg CALCIUM Group means and standard deviations Placebo group (n=11): 800 mg calcium supplement group (n=11) Mean spine BMD = .92 g/cm2 standard deviation = .10 g/cm2 Mean spine BMD = .94 g/cm2 standard deviation = .08 g/cm2 1500 mg calcium supplement group (n=11) Mean spine BMD =1.06 g/cm2 standard deviation = .11 g/cm2 The size of the groups. Between-group variation. The F-Test 2 sbetween The difference of each group’s mean from the overall mean. 2 2 2 (. 92 . 97 ) (. 94 . 97 ) ( 1 . 06 . 97 ) ns x2 11* ( ) .063 3 1 2 swithin avg s 2 1 (.102 .082 .112 ) .0095 3 F2,30 The average amount of variation within groups. 2 between 2 within s s .063 6.6 .0095 Large F value indicates Each group’s variance. that the between group variation exceeds the within group variation (=the background noise). Review Question 4 Which of the following is an assumption of ANOVA? a. The outcome variable is normally distributed. b. The variance of the outcome variable is the same in all groups. c. The groups are independent. d. All of the above. e. None of the above. Review Question 4 Which of the following is an assumption of ANOVA? a. The outcome variable is normally distributed. b. The variance of the outcome variable is the same in all groups. c. The groups are independent. d. All of the above. e. None of the above. ANOVA summary A statistically significant ANOVA (F-test) only tells you that at least two of the groups differ, but not which ones differ. Determining which groups differ (when it’s unclear) requires more sophisticated analyses to correct for the problem of multiple comparisons… Question: Why not just do 3 pairwise ttests? Answer: because, at an error rate of 5% each test, this means you have an overall chance of up to 1(.95)3= 14% of making a type-I error (if all 3 comparisons were independent) If you wanted to compare 6 groups, you’d have to do 15 pairwise ttests; which would give you a high chance of finding something significant just by chance. Multiple comparisons Correction for multiple comparisons How to correct for multiple comparisons post-hoc… • Bonferroni correction (adjusts p by most conservative amount; assuming all tests independent, divide p by the number of tests) • Tukey (adjusts p) • Scheffe (adjusts p) 1. Bonferroni For example, to make a Bonferroni correction, divide your desired alpha cut-off level (usually .05) by the number of comparisons you are making. Assumes complete independence between comparisons, which is way too conservative. Obtained P-value Original Alpha # tests New Alpha Significant? .001 .05 5 .010 Yes .011 .05 4 .013 Yes .019 .05 3 .017 No .032 .05 2 .025 No .048 .05 1 .050 Yes 2/3. Tukey and Sheffé Both methods increase your p-values to account for the fact that you’ve done multiple comparisons, but are less conservative than Bonferroni (let computer calculate for you!). Review Question 5 I am doing an RCT of 4 treatment regimens for blood pressure. At the end of the day, I compare blood pressures in the 4 groups using ANOVA. My p-value is .03. I conclude: a. b. c. d. All of the treatment regimens differ. I need to use a Bonferroni correction. One treatment is better than all the rest. At least one treatment is different from the others. e. In pairwise comparisons, no treatment will be Review Question 5 I am doing an RCT of 4 treatment regimens for blood pressure. At the end of the day, I compare blood pressures in the 4 groups using ANOVA. My p-value is .03. I conclude: a. b. c. d. All of the treatment regimens differ. I need to use a Bonferroni correction. One treatment is better than all the rest. At least one treatment is different from the others. e. In pairwise comparisons, no treatment will be Continuous outcome (means) Are the observations correlated? Outcome Variable Continuous (e.g. blood pressure, age, pain score) independent correlated Ttest: compares means Paired ttest: compares means between two independent groups ANOVA: compares means between more than two independent groups Pearson’s correlation coefficient (linear correlation): shows linear correlation between two continuous variables Linear regression: multivariate regression technique when the outcome is continuous; gives slopes or adjusted means between two related groups (e.g., the same subjects before and after) Repeated-measures ANOVA: compares changes over time in the means of two or more groups (repeated measurements) Mixed models/GEE modeling: multivariate regression techniques to compare changes over time between two or more groups Alternatives if the normality assumption is violated (and small n): Non-parametric statistics Wilcoxon sign-rank test: non-parametric alternative to paired ttest Wilcoxon sum-rank test (=Mann-Whitney U test): nonparametric alternative to the ttest Kruskal-Wallis test: non- parametric alternative to ANOVA Spearman rank correlation coefficient: non-parametric alternative to Pearson’s correlation coefficient Non-parametric ANOVA (Kruskal-Wallis test) Statistical question: Do nevi counts differ by training velocity (slow, medium, fast) group in marathon runners? What is the outcome variable? Nevi count What type of variable is it? Continuous Is it normally distributed? No (and small sample size) Are the observations correlated? No Are groups being compared and, if so, how many? Yes, three non-parametric ANOVA Example: Nevi counts and marathon runners Richtig et al. Melanoma Markers in Marathon Runners: Increase with Sun Exposure and Physical Strain. Dermatology 2008;217:38-44. Non-parametric ANOVA Kruskal-Wallis one-way ANOVA (just an extension of the Wilcoxon Sum-Rank test for 2 groups; based on ranks) Example: Nevi counts and marathon runners By non-parametric ANOVA, the groups differ significantly in nevi count (p<.05) overall. By Wilcoxon sum-rank test (adjusted for multiple comparisons), the lowest velocity group differs significantly from the highest velocity group (p<.05) Richtig et al. Melanoma Markers in Marathon Runners: Increase with Sun Exposure and Physical Strain. Dermatology 2008;217:38-44. Review Question 6 I want to compare depression scores between three groups, but I’m not sure if depression is normally distributed. What should I do? a. b. c. d. e. Don’t worry about it—run an ANOVA anyway. Test depression for normality. Use a Kruskal-Wallis (non-parametric) ANOVA. Nothing, I can’t do anything with these data. Run 3 nonparametric ttests. Review Question 6 I want to compare depression scores between three groups, but I’m not sure if depression is normally distributed. What should I do? a. b. c. d. e. Don’t worry about it—run an ANOVA anyway. Test depression for normality. Use a Kruskal-Wallis (non-parametric) ANOVA. Nothing, I can’t do anything with these data. Run 3 nonparametric ttests. Review Question 7 If depression score turns out to be very non-normal, then what should I do? a. b. c. d. e. Don’t worry about it—run an ANOVA anyway. Test depression for normality. Use a Kruskal-Wallis (non-parametric) ANOVA. Nothing, I can’t do anything with these data. Run 3 nonparametric ttests. Review Question 7 If depression score turns out to be very non-normal, then what should I do? a. Don’t worry about it—run an ANOVA anyway. b. Test depression for normality. c. Use a Kruskal-Wallis (non-parametric) ANOVA. d. Nothing, I can’t do anything with these data. e. Run 3 nonparametric ttests. Review Question 8 I measure blood pressure in a cohort of elderly men yearly for 3 years. To test whether or not their blood pressure changed over time, I compare the mean blood pressures in each time period using a one-way ANOVA. This strategy is: a. b. c. d. e. Correct. I have three means, so I have to use ANOVA. Wrong. Blood pressure is unlikely to be normally distributed. Wrong. The variance in BP is likely to greatly differ at the three time points. Correct. It would also be OK to use three ttests. Wrong. The samples are not independent. Review Question 8 I measure blood pressure in a cohort of elderly men yearly for 3 years. To test whether or not their blood pressure changed over time, I compare the mean blood pressures in each time period using a one-way ANOVA. This strategy is: a. b. c. d. e. Correct. I have three means, so I have to use ANOVA. Wrong. Blood pressure is unlikely to be normally distributed. Wrong. The variance in BP is likely to greatly differ at the three time points. Correct. It would also be OK to use three ttests. Wrong. The samples are not independent.