Download Non-Parametric Statistics

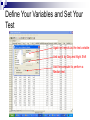
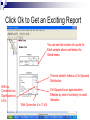
Non-Parametric
Statistics
©2005 Dr. B. C. Paul
The Normal Problem

Techniques we have used so far relied mostly on
underlying distribution to be normal
 We
have allowed some variables to be unordered
classes


For example the shifts and plants in the ANOVA example
We have found ways of checking whether our
distribution is normal and even ways to fit a
lognormal distribution.
 What
if the distribution is not normal or even close
enough for us to defend our use of normal statistics?
Common Causes of Non-Normal
Distribution

A normal distribution requires a continuous
quantitative distribution
 Some
data may not be continuous
ICE scores for faculty at the end of the semester
asks for integer input
 Numbers are ordered but not continuous
 Rankings may also have this property

Example

A large number of students go to take one of Dr. Paul’s
tests. Psychologists select 20 students at random and
analyze them for ability to recall basic facts






5= Unconscious before they could be ask their name
4 = Passed into unconsciousness when ask their name
3= could not remember their name
2= remembered their name when given a clue
1= able to remember their name without difficulty
Of the 20 students, 18 of them were given a rank of 1, 1
was given a rank of 4, and 1 was given a rank of 2.
Example Continued



After 3 hours taking the test the psychologists dragged 20 people
from their seats for testing
5 were given a rank of 5 (one psychologist suggested a 6 should be
added to the scale for already dead to differentiate 1 student from
the other 4), 3 were given a rank of 4, 2 were given a rank of 3, 7
were given a rank of 2, and 2 were given a rank of 1.
The pyscologist’s null hypothesis is that exposure to one of Dr.
Paul’s tests has no effect on the ability of students to recall basic
facts, rejecting the null hypothesis would imply that exposure to one
of Dr. Paul’s tests has a brain frying effect that erodes the ability of
the victim – woops I mean student to recall basic facts.
The Problem

The numbers 1 to 5 (or 6) are ordered, but
they are categories rather than continuous
numbers
 Data
of this type cannot meet the continuous
variable requirements of a normal distribution
Other Causes of Non-Normal
Problems with the tails – or skewness
 Some distributions simply are not normal

 Accidents
often have a Weibull Distribution
There Are Statistical Options


Non-Parametric Statistics
Measuring Central Tendency
 Normal
distribution can measure with the mean (since
its symmetric)
 Median – or 50% value is center of a more general
distribution

Measuring Dispersion
 Can calculate a standard deviation for anything
 Cumulative shape and area under curve is more
characteristic of a general distribution.
Consequences of Going NonParametric

We measure basic properties of distributions in ways
that are less universally understood



Median instead of Mean
Shape instead of standard deviation
We loose power to tell close calls without greater
numbers of samples


Saw the Brehens Fisher T test loose power
Confidence intervals and tests are still based on what
percentage of the probability distribution is beyond a certain
point



For normal distribution over 95% is within 2 standard deviations
For general distribution 75% is within 2 standard deviations
Result is a much wider range of uncertainty in Non-Parametric
Power of a Test

We have an aversion to rejecting truth

That’s what the null hypothesis bit is about


Flip Side is we would like to be able to reject falsehood
with reasonable samples


This is measured by “Power”
Power of a test is indicated by how close two different peaks or
quantities can be and the test still tell them apart


If you don’t have a lot of evidence don’t reject idea that nothing is
happening.
Those wider limits on non-parametric tests cause them to have
much less power
Of course using a false model of a distribution to get a
powerful test is just fooling ourselves
Suppose we want to compare the
number of rejects on day and night
shift

Suppose we do not believe that our
distribution is normal
 This
would prevent us from doing a T test like
we did before

Mann-Whitney Test is available
Assumptions of the Mann Whitney
Test


Two independent random samples
The variable being measured is ordered
 The scale need not be continuous
 But the numbers must be ordered 5>4

etc
The populations sampled differ only in location if
they differ at all
 This
means the two samples have to come from the
same type of distribution
 It also means that the dispersion of those populations
must be the same
Running a Mann Whitney Test
Click Analyze for the Pull
Down Menu
Highlight NonParametric Tests
To bring up the pop out menu
Highlight and click two
Independent samples.
Set the Variables
Select the number of rejects
Per 1000 as the test variable
Group it by Day and Night Shift
Set the tests to be run
I’ll order Mann Whitney,
Kolmogorov-Smirnov
And WaldWolfowitz runs.
Click Ok and Out Comes A Report
Understanding the Ranking Stuff
Mann-Whitney pools the two samples
And assigns rank order to each sample
Value. It then counts the rank order sum
For each sample or the number of times
That one sample set beats another.
If two samples of identical shape have
The same central tendency location then
Those ranks or the sum of ranks should
Be about the same.
If one sample is shifted relative to the
Other the rank sums will be screwy.
Checking Out the Result
The counted sums are displayed
As U and W statistics
They can be matched to a
Standard normal distribution with
The right formulas (Z statistic)
Mann Whitney assigns average
Rank to ties but then you only
Approximately get a Normal
Distribution
You can get an exact normal
Distribution but then who wins in
A tie is a luck of the draw.
Bottom Line Significance is there is around an 8.5% chance that this could be an
Accident and the shifts be the same.
The Outcome
Quincy was able to go kick the night shift
in the wotusee with the T test
 The 5% significance normally needed to
reject the null hypothesis was not
achieved with the Mann Whitney

 Non-Parametric
Statistics lack the power
achieved by normal statistics
Assumption Validity

Mann Whitney required us to assume that we
had two same shaped distributions
 From
Levene’s test we did when we were looking at
dispersion we suspect this might be wrong
 If one population is more dispersed than the other it
may have ranks spread all through the other
population even though the center is somewhere else

Mann Whitney did not reject the null hypothesis
but we might have violated the test assumption
and got an invalid result.
So What About that Dispersion
Issue

We know that Levene’s test says the two shifts
have different dispersions
 But
if we won’t make a normal distribution assumption
Levene’s test may not be valid

We have a non-parametric test for shape of
distribution
 Note that the test is not strictly for dispersion
 Test can work because if two same types of
distributions have different dispersions their shapes
will be different
 Kolmogorov-Smirnov Test
Kolmogorov-Smirnov

We remember using this test to determine if a sample
came from a certain type of distribution



If normalized sample set follows a normal distribution
then the sample set will not depart much from the normal
distribution


The test works by looking at the cumulative probability for two
distributions up to a point
It uses the greatest gap as the test statistic
We used that to see if we had a normal distribution
In fact we could use that to find out whether a sample set
matched any distribution what-so-ever

Which is what we are trying to do here to see if one distribution
is more dispersed than the other.
Looking at the Results
The significance of the K-S Test is
1.3% ie
We are pretty darn sure that these
Two data sets have a different shape.
Assuming they are about the same
Type of shape that would mean the
Dispersion is different.
Unfortunate Assumptions

The Kolmogorov-Smirnov Test assumes that the two
distributions have the same median value


If two identical distributions have different means obviously you
will get large departures in the number of values less than 5 or 7
etc.
To make K-S work as a good dispersion test you have to
correct for shifts in the means


Some people do this test by looking at the calculated mean and
then shifting one data set to make the means of the data sets
have the same value
Kind of cheating but it does focus the sample set differences in
on what you wanted.
Looking at Our Last Test
Wald Wolfowitz test also works off
Of rank order. It looks at the
Number of rank orders in a row
Captured the each distribution.
If the sample sets come from
Populations that are pretty much
The same then the ranks captured
Will be about the same for each
Sample and we will end up with
A bunch of short runs
Ie – Big numbers suggest the
Populations are the same
Little ones suggest something
Strange
The Tie Issue
Our computer calculates the
Number of runs with or without
Handling ties.
If a tie breaks a run then you have
More runs than if it takes a
Clear win to break a run
If we allow ties to break a run
We have 13.1% significance and
Cannot reject the null hypothesis
If ties don’t break there is
Something wrong with the null
Hypothesis.
What Does the WaldWolfowitz Test
Tell Us

1- Non-parametric tests can perform badly when
ties occur
 We
can get essential certainty to 13.1% risk on
rejecting the null hypothesis just from deciding
whether a tie breaks a run

If we reject the null hypothesis Wald Wolfowitz is
still spongy on meaning
 Actually
turns out the test is rather poor on power to
Wald Wolfowitz is a Vague Test
Rejecting the null hypothesis means that
we reject that the two populations were the
same
 Now the only question is how were they
different

 Could
be location
 Could be type of distribution
 Could be dispersion
The Vague Problem with NonParametrics

Tests kind of test whether populations are
different
 Use

assumptions to tell whats different
Mann Whitney tests equivalence of the median
 But
only if you can eliminate differences in type of
distribution and dispersion

K-S will test shape
 If
you can assume same type of shape and same
median it will work for testing dispersion

Wald-Wolfowitz can’t be tuned to anything
Our Dilemma




We can’t get a good test on the median because we
don’t know if the dispersion is the same
We can’t get a good test on the dispersion because the
mean may be different
(In fact we have a hunch that both the mean and the
dispersion are different)
We could adjust for observed differences in median and
get a good test for dispersion out of the KS test


When we got a null hypothesis rejection we would then have
invalidated our Mann Whitney test
And Wald Wolfowitz would be inconclusive about location of the
median
Another Alternative

The Median test
 Works
by comparing how many values each sample
has above or below the grand median for both
combined
 If the medians are the same then the proportion of
each above the grand median should be about the
same

The test is less powerful than Mann Whitney but
it is insensitive to differences in shape and
dispersion of the two populations
How to do a Median Test
As before pull down analyze
And highlight Non Parametric
Tests
This time highlight and click K
Independent samples.
Define Your Variables and Set Your
Test
Again set rejects as the test variable
And sort it by Day and Night Shift
Ask the computer to perform a
Median test.
Click Ok to Get an Exciting Report
You can see the number of counts for
Each sample above and below the
Grand mean.
The test statistic follows a Chi-Squared
Distribution
With no
Correction our
Significance is
5.8%
Chi-Squared is an approximation
Effected by lack of continuity in small
Samples.
With Correction it is 11.4%
Bottom Line Interpretations




The Median test was more conclusive than Mann
Whitney where we were affected by the difference in
dispersion
Unfortunately we still fell short of ability to reject at the
5% confidence level
Some people today would call 5.8% close enough and
would move to do something about the night shift.
You can clearly see that Non-Parametrics allows you to
work with problems where normal statistics stop applying

But we do so with a distinct loss of power in the test