* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Non-Parametric Statistics
Survey
Document related concepts
Transcript
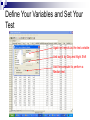
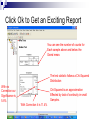
Non-Parametric Statistics ©2005 Dr. B. C. Paul The Normal Problem Techniques we have used so far relied mostly on underlying distribution to be normal We have allowed some variables to be unordered classes For example the shifts and plants in the ANOVA example We have found ways of checking whether our distribution is normal and even ways to fit a lognormal distribution. What if the distribution is not normal or even close enough for us to defend our use of normal statistics? Common Causes of Non-Normal Distribution A normal distribution requires a continuous quantitative distribution Some data may not be continuous ICE scores for faculty at the end of the semester asks for integer input Numbers are ordered but not continuous Rankings may also have this property Example A large number of students go to take one of Dr. Paul’s tests. Psychologists select 20 students at random and analyze them for ability to recall basic facts 5= Unconscious before they could be ask their name 4 = Passed into unconsciousness when ask their name 3= could not remember their name 2= remembered their name when given a clue 1= able to remember their name without difficulty Of the 20 students, 18 of them were given a rank of 1, 1 was given a rank of 4, and 1 was given a rank of 2. Example Continued After 3 hours taking the test the psychologists dragged 20 people from their seats for testing 5 were given a rank of 5 (one psychologist suggested a 6 should be added to the scale for already dead to differentiate 1 student from the other 4), 3 were given a rank of 4, 2 were given a rank of 3, 7 were given a rank of 2, and 2 were given a rank of 1. The pyscologist’s null hypothesis is that exposure to one of Dr. Paul’s tests has no effect on the ability of students to recall basic facts, rejecting the null hypothesis would imply that exposure to one of Dr. Paul’s tests has a brain frying effect that erodes the ability of the victim – woops I mean student to recall basic facts. The Problem The numbers 1 to 5 (or 6) are ordered, but they are categories rather than continuous numbers Data of this type cannot meet the continuous variable requirements of a normal distribution Other Causes of Non-Normal Problems with the tails – or skewness Some distributions simply are not normal Accidents often have a Weibull Distribution There Are Statistical Options Non-Parametric Statistics Measuring Central Tendency Normal distribution can measure with the mean (since its symmetric) Median – or 50% value is center of a more general distribution Measuring Dispersion Can calculate a standard deviation for anything Cumulative shape and area under curve is more characteristic of a general distribution. Consequences of Going NonParametric We measure basic properties of distributions in ways that are less universally understood Median instead of Mean Shape instead of standard deviation We loose power to tell close calls without greater numbers of samples Saw the Brehens Fisher T test loose power Confidence intervals and tests are still based on what percentage of the probability distribution is beyond a certain point For normal distribution over 95% is within 2 standard deviations For general distribution 75% is within 2 standard deviations Result is a much wider range of uncertainty in Non-Parametric Power of a Test We have an aversion to rejecting truth That’s what the null hypothesis bit is about Flip Side is we would like to be able to reject falsehood with reasonable samples This is measured by “Power” Power of a test is indicated by how close two different peaks or quantities can be and the test still tell them apart If you don’t have a lot of evidence don’t reject idea that nothing is happening. Those wider limits on non-parametric tests cause them to have much less power Of course using a false model of a distribution to get a powerful test is just fooling ourselves Suppose we want to compare the number of rejects on day and night shift Suppose we do not believe that our distribution is normal This would prevent us from doing a T test like we did before Mann-Whitney Test is available Assumptions of the Mann Whitney Test Two independent random samples The variable being measured is ordered The scale need not be continuous But the numbers must be ordered 5>4 etc The populations sampled differ only in location if they differ at all This means the two samples have to come from the same type of distribution It also means that the dispersion of those populations must be the same Running a Mann Whitney Test Click Analyze for the Pull Down Menu Highlight NonParametric Tests To bring up the pop out menu Highlight and click two Independent samples. Set the Variables Select the number of rejects Per 1000 as the test variable Group it by Day and Night Shift Set the tests to be run I’ll order Mann Whitney, Kolmogorov-Smirnov And WaldWolfowitz runs. Click Ok and Out Comes A Report Understanding the Ranking Stuff Mann-Whitney pools the two samples And assigns rank order to each sample Value. It then counts the rank order sum For each sample or the number of times That one sample set beats another. If two samples of identical shape have The same central tendency location then Those ranks or the sum of ranks should Be about the same. If one sample is shifted relative to the Other the rank sums will be screwy. Checking Out the Result The counted sums are displayed As U and W statistics They can be matched to a Standard normal distribution with The right formulas (Z statistic) Mann Whitney assigns average Rank to ties but then you only Approximately get a Normal Distribution You can get an exact normal Distribution but then who wins in A tie is a luck of the draw. Bottom Line Significance is there is around an 8.5% chance that this could be an Accident and the shifts be the same. The Outcome Quincy was able to go kick the night shift in the wotusee with the T test The 5% significance normally needed to reject the null hypothesis was not achieved with the Mann Whitney Non-Parametric Statistics lack the power achieved by normal statistics Assumption Validity Mann Whitney required us to assume that we had two same shaped distributions From Levene’s test we did when we were looking at dispersion we suspect this might be wrong If one population is more dispersed than the other it may have ranks spread all through the other population even though the center is somewhere else Mann Whitney did not reject the null hypothesis but we might have violated the test assumption and got an invalid result. So What About that Dispersion Issue We know that Levene’s test says the two shifts have different dispersions But if we won’t make a normal distribution assumption Levene’s test may not be valid We have a non-parametric test for shape of distribution Note that the test is not strictly for dispersion Test can work because if two same types of distributions have different dispersions their shapes will be different Kolmogorov-Smirnov Test Kolmogorov-Smirnov We remember using this test to determine if a sample came from a certain type of distribution If normalized sample set follows a normal distribution then the sample set will not depart much from the normal distribution The test works by looking at the cumulative probability for two distributions up to a point It uses the greatest gap as the test statistic We used that to see if we had a normal distribution In fact we could use that to find out whether a sample set matched any distribution what-so-ever Which is what we are trying to do here to see if one distribution is more dispersed than the other. Looking at the Results The significance of the K-S Test is 1.3% ie We are pretty darn sure that these Two data sets have a different shape. Assuming they are about the same Type of shape that would mean the Dispersion is different. Unfortunate Assumptions The Kolmogorov-Smirnov Test assumes that the two distributions have the same median value If two identical distributions have different means obviously you will get large departures in the number of values less than 5 or 7 etc. To make K-S work as a good dispersion test you have to correct for shifts in the means Some people do this test by looking at the calculated mean and then shifting one data set to make the means of the data sets have the same value Kind of cheating but it does focus the sample set differences in on what you wanted. Looking at Our Last Test Wald Wolfowitz test also works off Of rank order. It looks at the Number of rank orders in a row Captured the each distribution. If the sample sets come from Populations that are pretty much The same then the ranks captured Will be about the same for each Sample and we will end up with A bunch of short runs Ie – Big numbers suggest the Populations are the same Little ones suggest something Strange The Tie Issue Our computer calculates the Number of runs with or without Handling ties. If a tie breaks a run then you have More runs than if it takes a Clear win to break a run If we allow ties to break a run We have 13.1% significance and Cannot reject the null hypothesis If ties don’t break there is Something wrong with the null Hypothesis. What Does the WaldWolfowitz Test Tell Us 1- Non-parametric tests can perform badly when ties occur We can get essential certainty to 13.1% risk on rejecting the null hypothesis just from deciding whether a tie breaks a run If we reject the null hypothesis Wald Wolfowitz is still spongy on meaning Actually turns out the test is rather poor on power to Wald Wolfowitz is a Vague Test Rejecting the null hypothesis means that we reject that the two populations were the same Now the only question is how were they different Could be location Could be type of distribution Could be dispersion The Vague Problem with NonParametrics Tests kind of test whether populations are different Use assumptions to tell whats different Mann Whitney tests equivalence of the median But only if you can eliminate differences in type of distribution and dispersion K-S will test shape If you can assume same type of shape and same median it will work for testing dispersion Wald-Wolfowitz can’t be tuned to anything Our Dilemma We can’t get a good test on the median because we don’t know if the dispersion is the same We can’t get a good test on the dispersion because the mean may be different (In fact we have a hunch that both the mean and the dispersion are different) We could adjust for observed differences in median and get a good test for dispersion out of the KS test When we got a null hypothesis rejection we would then have invalidated our Mann Whitney test And Wald Wolfowitz would be inconclusive about location of the median Another Alternative The Median test Works by comparing how many values each sample has above or below the grand median for both combined If the medians are the same then the proportion of each above the grand median should be about the same The test is less powerful than Mann Whitney but it is insensitive to differences in shape and dispersion of the two populations How to do a Median Test As before pull down analyze And highlight Non Parametric Tests This time highlight and click K Independent samples. Define Your Variables and Set Your Test Again set rejects as the test variable And sort it by Day and Night Shift Ask the computer to perform a Median test. Click Ok to Get an Exciting Report You can see the number of counts for Each sample above and below the Grand mean. The test statistic follows a Chi-Squared Distribution With no Correction our Significance is 5.8% Chi-Squared is an approximation Effected by lack of continuity in small Samples. With Correction it is 11.4% Bottom Line Interpretations The Median test was more conclusive than Mann Whitney where we were affected by the difference in dispersion Unfortunately we still fell short of ability to reject at the 5% confidence level Some people today would call 5.8% close enough and would move to do something about the night shift. You can clearly see that Non-Parametrics allows you to work with problems where normal statistics stop applying But we do so with a distinct loss of power in the test