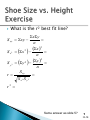* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Six Sigma Class
Survey
Document related concepts
Transcript
1 We first looked at this for the regression analysis. Introduction to (DOE) – one factor test Develops a model relating a response to a factor - allows prediction of responses at levels other than where data was collected ◦ quantifies the strength of the model ◦ identifies outliers Uses terminology involved in simple linear regression ◦ ◦ ◦ ◦ Intercept Slope Prediction Equation Y = f(X) R-squared X Y 2 IX-8 Draw a “best fit” line through the data Place the values you found for bo and b1 in the following template. y= Where + X bo b1 bo = y-intercept b1 = slope = Rise/Run 3 IX-9 xy S xy xy n 2 x S x 2 x 2 n S xy b1 S x2 b 0 y b1 x yˆ b 0 b 1 x 4 IX-12 How tall do we predict someone would be if their shoe size is 9.5? 5 IX-12 r 2 ‘Correlation’ is a fancy word for how well the model predicts the response from the factors. 6 IX-18 What is the r² best fit line? S xy xy S x 2 x 2 S y 2 y 2 r xy n 2 x n 2 y n S xy S x2 S y2 r2 Same answer as slide 5? 7 IX-18 8 IX-18 Did your project reduce variation or shift the mean? How do you demonstrate improvements statistically 9 IX-24 The question one needs to ask during a project is whether the changes made as the result of a Green Belt project have made a difference in the process. The question is, “Has the project made a difference, and if so, how confident are we that the difference is statistically significant?” We strive for 95% confidence or better (α=.05). 10 IX-24 A hypothesis is: Examples: ◦ a tentative explanation for an observation that can be tested by further investigation. ◦ taken to be true for the purpose of investigation; an assumption. ◦ Average gas mileage differs depending on type A or B gas. ◦ Probability of death in auto accidents differs depending on seat belt usage. ◦ The type of aspirin determines the amount of pain relief. ◦ A Six Sigma Green Belt project produced significant results with regard to mean and/or standard deviation improvement. 11 IX-24 We set up 2 hypotheses ◦ H0 is called the null hypothesis what is being tested must contain an = assumed to be true ◦ H1 is called the alternate hypothesis Based on the data we collect, we must decide in favor of either H0 or H1. Which does the evidence support? ◦ can only reject null, or fail to reject null 12 IX-24 Define the problem and state objectives State a “Null Hypothesis” (Ho) State the “Alternative Hypothesis” (H1) Establish significance level (a) and determine the critical value Collect sample data Calculate test statistic and/or p-value DECIDE: What does the evidence suggest? Reject Ho? or Fail to reject Ho? 13 IX-27 Based on a normal distribution Z values from the Standard Normal table Za / 2 (ˆ ) n errorlevel 2 n = sample size Za/2 = 1.96 for 95% confidence = 2.576 for 99% confidence ̂ = estimated standard deviation error level = amount of error allowed (i.e. to estimate within +/-2 standard deviation, the half interval width is 2) 14 IX-31 A test on cigarettes yielded an average nicotine content of 15.6 milligrams and a standard deviation of 2.1 milligrams. If we want to be 99% confident in detecting a 1 milligram change, what sample size would be required? What if we only want to be 95% confident? 15 IX-31 Based on a binomial distribution ( Z a / 2 ) 2 p(1 p) n 2 (p) n = sample size Za/2 = 1.96 for 95% confidence = 2.576 for 99% confidence p = average proportion defectives 1 p = q (proportion non-defectives) p = amount of error allowed 16 IX-31 You have just received a shipment of computer memory chips. Suppose we wanted to have 95% confidence with detecting a change of 1%. Assuming the historical proportion of defectives in no more than 2%, what sample size would be required? 17 IX-31 Up to this point we have talked about point estimators (mean, standard deviation, etc) these represent population parameters. We can also construct an interval that has a predetermined probability of including the true population parameter (). This is a confidence interval. 18 IX-34 A test on a random sample of 9 cigarettes yielded an average nicotine content of 15.6 milligrams and a standard deviation of 2.1 milligrams. Construct a 99% confidence interval for the true average nicotine content. What if we only want 95% confidence? What happens to the 99% confidence interval if we had tested 30 cigarettes originally? 19 IX-35 You have just received a shipment of computer memory chips. From a sample of 100 chips, you find 6 to be defective. Find a 95% confidence interval for the true but unknown proportion of defective chips in the shipment. What if we want 99% confidence? 20 IX-36 1. 2. 3. 4. 5. 6. Let’s set the Statapult up and take some data. Set the Statapult up and reduce variation as much as possible. Confirm with >25 shots. Calculate and record average . Choose a condition to test that you expect will make a difference in the mean. Use two inspectors. Record each inspectors answers separately. Fire 10 shots with the new setting. Calculate sample average, X-bar and sample standard deviation from one of the inspectors. Save the other inspector data for a later example. (1) Create a hypothesis test to determine if the changed condition results in a statistical difference. (2) Determine if there is a difference between the two inspectors. 21 IX-45 1. 2. 3. 4. Let’s set the Statapult up and take some data. Set the Statapult up and reduce variation as much as possible. Confirm with 10 shots. Calculate and record sample standard deviation s, and variance s². Choose a condition to test that you expect will make a difference in the variation. Shoot 10 shots with the new condition and calculate sample standard deviation s, and variance s². Create a hypothesis test to determine if the changed condition results in a statistical difference. 22 IX-48