Download Chapter 11 - Lecture 1

Experiments show O2 is paramagnetic
MOLECULAR STRUCTURE
CHAPTER 11

Objectives:

Extend atomic concepts to electronic
structures of molecules

Utilize two quantum mechanical
theories of molecular electronic structure

Valence bond theory


Bonding as a result of a shared
electron pair between two atoms
Molecular orbital theory

Concept of atomic orbital extended to
molecular orbital

Molecular orbital is a wavefunction
spread over entire molecule
Fig 11.1 A molecular potential energy curve
Equilibrium bond length
Depth of well
v=0
Dissociation energy, Do
Do = De -
1/2ћω
Change in electron
density as two hydrogen
atoms approach each
other.
Fig 11.2 Representations of valence-bond
wavefunctions
Electron 1
Electron 2
A
B
Molecular potential energy curve for H2
Ψ(1,2) = {A(1)B(2) + A(2)B(1)} σ(1,2)
According to Pauli principle: Ψ(1,2) = -Ψ(2,1)
∴ σ(1,2) = - σ(2,1)
and σ(1,2) = √1/2{α(1)β(2) - α(2)β(1)}
with valence-bond model
a singlet state
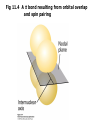
Fig 11.3 Orbital overlap and spin pairing in two
collinear p orbitals to form a σ bond
Fig 11.4 A
π bond resulting from orbital overlap
and spin pairing
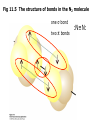
Fig 11.5 The structure of bonds in the N2 molecule
one σ bond
two
π bonds
:N≡N:
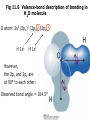
Fig 11.6 Valence-bond description of bonding in
H2O molecule
O atom: 2s2 (2px)2 (2py)1 (2pz)1
H 1s1
H 1s1
However,
the 2py and 2pz are
at 90° to each other:
Observed bond angle = 104.5°
Hybridization – mixing of two or more atomic orbitals to form
a new set of hybrid orbitals.
1. Mix at least 2 nonequivalent atomic orbitals (e.g. s and p).
Hybrid orbitals have very different shape from original
atomic orbitals.
2. Number of hybrid orbitals is equal to number of pure atomic
orbitals used in the hybridization process.
3. Covalent bonds are formed by:
a. Overlap of hybrid orbitals with atomic orbitals or
b. Overlap of hybrid orbitals with other hybrid orbitals
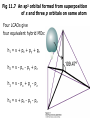
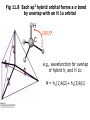
Fig 11.7 An sp3 orbital formed from superposition
of s and three p orbitals on same atom
Four LCAOs give
four equivalent hybrid MOs:
h 1 = s + px + p y + pz
h 2 = s - px - py + pz
h 3 = s - px + p y - pz
h 4 = s + px - p y - pz
Fig 11.8 Each sp3 hybrid orbital forms a σ bond
by overlap with an H 1s orbital
109.5°
e.g., wavefunction for overlap
of hybrid h1 and H 1s:
Ψ = h1(1)A(2)+ h1(2)A(1)
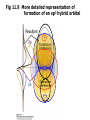
Fig 11.9 More detailed representation of
formation of an sp3 hybrid orbital
Fig 11.10 An sp2 orbital formed from superposition
of s and two p orbitals on same atom
Three LCAOs give
three equivalent hybrid MOs:
h1 = s + √1/2 py
h2 = s + √3/2 px - √1/2 py
h3 = s - √3/2 px - √1/2 py
Remaining unhybridized p orbital
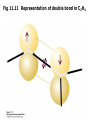
Fig 11.11 Representation of double bond in C2H4
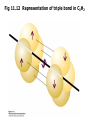
Fig 11.12 Representation of triple bond in C2H2
How do I predict the hybridization of the central atom?
Count the number of lone pairs AND the number
of atoms bonded to the central atom
# of Lone Pairs
+
# of Bonded Atoms
Hybridization
Examples
2
sp
BeCl2
3
sp2
BF3
4
sp3
CH4, NH3, H2O
5
sp3d
PCl5
6
sp3d2
SF6