* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download hash table
Survey
Document related concepts
Transcript
GRIFFITH
COLLEGE
DUBLIN
Data Structures, Algorithms &
Complexity
Hash Tables
Lecture 6
1
Introduction
Many applications require a data structure that
supports only the dictionary operations Insert,
Search, Delete
For example, a compiler maintains a symbol table, in
which the keys of the elements are arbitrary
character strings that correspond to the identifiers of
the language
A Hash Table is an effective data structure for
implementing dictionaries
Lecture 6
2
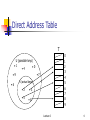
Direct Addressing
An application needs a dynamic set in which each
element has a key drawn from the universe U = {0,
1,…., m-1}, where m is not too large
We assume that no two elements have the same key
We can represent the set using an array, or directaddress-table, T[0..m-1] in which each position, or
slot, corresponds to a key in the universe U.
Searching such a structure on the key involves (1)
time
Lecture 6
3
Direct Address Table
T
0
1
2
3
4
5
6
7
8
9
U (possible keys)
1
0
•4
•7
9
•6
K (actual keys)
•2
•5
•3
•8
Lecture 6
4
Difficulties
The difficulties with direct addressing are obvious
If the Universe is large, then having a table of size
|U| may be impractical.
Also, the set K of keys actually stored may be so
small relative to U that most of the space allocated
for T would be wasted
Hash tables are designed to deal specifically with this
problem which is a common occurrence
Lecture 6
5
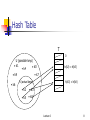
Hash Tables
With direct addressing, an element with key k is
stored in slot k.
With hashing , this element is stored in slot h(k),
where h(k) is a hash function used to compute the
slot from the key k.
Here h maps the universe U of keys into the slots of
a hash table T[0..m-1]
h: U {0, 1, …., m-1}
We say that an element with key k hashes to slot
h(k)
Lecture 6
6
Hash Tables
The point of the hash function is to reduce the range
of array indices that need to be handled.
Instead of reserving memory space for |U| values,
we need to handle only m values so reducing storage
The main problem with this scheme is that two
values may hash to the same slot, a collision
There are a number of techniques available to handle
collisions
Since |U| > m, we cannot avoid collisions
Lecture 6
7
Hash Table
T
0
U (possible keys)
k1
k0
• k4
• k7
k9
• k6
h(k2) = h(k5)
K (actual keys)
• k2
• k5
h(k3) = h(k8)
• k3
• k8
Lecture 6
8
Collision Resolution by Chaining
Chaining is one of the simplest collision resolution
techniques
In chaining we put all the elements that hash to the
same slot in a linked list
Slot j contains a reference to the head of a list of all
the elements that hash to j
If there are no items then the reference is nil
Lecture 6
9
Collision Resolution - Chaining
T
U (possible keys)
k1
k0
• k4
• k7
k9
• k6
k2
K (actual keys)
• k2
• k5
k3
k5
k8
• k3
• k8
Lecture 6
10
Analysis of Hashing
The worst case is where all elements hash to the
same slot, making the search (n) plus the time to
calculate the hash function
This is no better than using a simple linked list
The average performance of hashing depends on
how well the has function distributes the set of keys
among the m slots on average
If we assume that any given element is equally likely
to hash into any of the m slots we call this
assumption simple uniform hashing
Lecture 6
11
The Division Method
In this method for creating hash functions, we map a key k into
one of m slots by using the remainder of k divided by m
h(k) = k mod m
Since it requires only one division operation, hashing by division
is quite fast
We usually avoid certain values of m
For example, m should not be a power of 2
The lower order bits of the key will dominate
This will lead to many collisions
Good values of m are primes not too close to exact powers of 2
Lecture 6
12
The Multiplication Method
This operates in two steps
Multiply the key k by a constant A in the range
0 < A < 1 and extract the fractional part of kA
Multiply this value by m and take the floor of the
result
h(k) = m(k A mod 1)
The advantage of this method is that the value of m
is not critical
Lecture 6
13
Open Addressing
In open addressing all elements are stored in the
hash table itself.
That is, no lists. To insert an element we
successively examine, or probe, the hash table until
we find an empty slot
So, we require that for every key, the probe sequence
<h(k,0), h(k,1),..h(k,m-1)> must be a permutation of
<0, 1, .. , m-1> to ensure every slot is tried as the
table fills up.
Each slot contains either a key value or nil
Lecture 6
14
Open Addressing
Hash-Insert(T,k)
i=0
repeat j = h(k,i)
if T[j] = nil then
return j
else i = i + 1
until i = m
error “hash table overflow”
endalg
Lecture 6
15
Open Addressing
If we have the search algorithm probe the same sequence of
slots that the insertion algorithm examined, we can terminate
the search if we find an empty slot, as this must mean the item
is not present
Hash-Search(T, k)
i=0
repeat j = h(k, i)
if T[j] = k then
return j
endif
i=i+1
until T[j] = nil or i = m
return nil
endalg
Lecture 6
16
Open Addressing
Deletion is difficult from an open addressing system
The problem is that if we simply mark the slot nil,
then it is impossible to retrieve any key whose
insertion probed that slot
One solution is to have a special ‘deleted’ value put
into such slots
When deletion is going to be a large factor, chaining
is often used.
Lecture 6
17
Probing
To improve efficiency a lot of work has gone into
devising good probing techniques.
These include
Linear Probing – simply trying consecutive slots
until an empty one is found – can suffer from
primary clustering
Quadratic Probing – use a quadratic function to
choose next slot to probe – can suffer from
secondary clustering
Double Hashing – a combination of two hash
functions – avoids clustering
Lecture 6
18
Summary
Hash tables are used to store data when the number
of keys is small relative to the range of the keys
Hash tables map all keys from a universal set to a
smaller set of slots
Collisions occur when two keys hash to the same slot
Chaining is one method of solution
Open Addressing with probing is another
Much research has gone into ensuring a uniform
distribution of the keys over the slots available.
Lecture 6
19