* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Bayesian Networks - Blog of Applied Algorithm Lab., KAIST
Survey
Document related concepts
Transcript
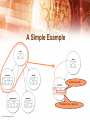
The slides are based on <Data Mining : Practical Learning Tools and Techniques>, 2nd ed., written by Ian H. Witten & Eibe Frank. Images and Materials are from the official lecture slides of the book. Bayesian Networks 4th, December 2009 Presented by Kwak, Nam-ju Table of Contents • • • • • • • • • • • • Probability Estimate vs. Prediction What is Bayesian Network? A Simple Example A Complex One Why does it work? Learning Bayesian Networks Overfitting Searching for a Good Network Structure K2 Algorithm Other Algorithms Conditional Likelihood Data Structures for Fast Learning Probability Estimate vs. Prediction • Naïve Bayes classifier, logistic regression models: probability estimates • For each class, they estimate the probability that a given instance belongs to that class. Probability Estimate vs. Prediction • Why probability estimates are useful? – They allow predictions to be ranked. – Treat classification learning as the task of learning class probability estimates from the data. • What is being estimated is – The conditional probability distribution of the values of the class attribute given the values of the other attributes. Probability Estimate vs. Prediction • In this way, Naïve Bayes classifiers, logistic regression models and decision trees are ways of representing a conditional probability distribution. What is Bayesian Network? • A theoretically well-founded way of representing probability distributions concisely and comprehensively in a graphical manner. • They are drawn as a network of nodes, one for each attribute, connected by directed edges in such a way that there are no cycles. – A directed acyclic graph A Simple Example Summed up into 1 Pr[outlook=rainy | play=no] A Complex One • When outlook=rainy, temperature=cool, humidity=high, and windy=true… • Let’s call E the situation given above. A Complex One • E: rainy, cool, high, and true • Pr[play=no, E] = 0.0025 • Pr[play=yes, E] = 0.0077 An additional example of the calculation Multiply all those!! A Complex One • E: rainy, cool, high, and true • Pr[play=no, E] = 0.0025 • Pr[play=yes, E] = 0.0077 A Complex One Summed up into 1 Why does it work? • Terminologies – T: all the nodes, P: parents, D: descendant Non-descendants – Non-descendant: T-D Why does it work? • Assumption (conditional independence) – Pr[node | parents plus any other set of non-descendants] = Pr[node | parents] • Chain rule • The nodes are ordered to give all ancestors of a node ai indices smaller than i. It’s possible since the network is acyclic. Why does it work? Ok, that’s what I’m talking about!!! Learning Bayesian Networks • Basic components of algorithms for learning Bayesian networks: – Methods for evaluating the goodness of a given network – Methods for searching through space of possible networks Learning Bayesian Networks • Methods for evaluating the goodness of a given network – Calculate the probability that the network accords to each instance and multiply these probabilities all together. – Alternatively, use the sum of logarithms. • Methods for searching through space of possible networks – Search through the space of possible sets of edges. Overfitting • While maximizing the log-likelihood based on the training data, the resulting network may overfit. What are the solutions? – Cross-validation: training instances and validation instances (similar to ‘early stopping’ in learning of neural networks) – Penalty for the complexity of the network – Assign a prior distribution over network structures and find the most likely network using the probability by the data. Overfitting • Penalty for the complexity of the network – Based on the total # of independent estimates in all the probability tables, which is called the # of parameters Overfitting • Penalty for the complexity of the network – K: the # of parameters – LL: log-likelihood Akaike Information – N: the # of instances in the training data Criterion – AIC score = -LL+K – MDL score = -LL+(K/2)logN Minimum Description Length – Those two scores are supposed to be minimized. Overfitting • Assign a prior distribution over network structures and find the most likely network by combining its prior probability with the probability accorded to the network by the data. Searching for a Good Network Structure • The probability of a single instance is the product of all the individual probabilities from the various conditional probability tables. • The product can be rewritten to group together all factors relating to the same table. • Log-likelihood can also be grouped in such a way. Searching for a Good Network Structure • Therefore log-likelihood can be optimized separately for each node. • This can be done by adding, or removing edges from other nodes to the node being optimized. (without making cycles) Which one is the best? Searching for a Good Network Structure • AIC and MDL can be dealt with in a similar way since they can be split into several components, one for each node. K2 Algorithm • Starts with given ordering of nodes (attributes) Result depends on the initial order • Processes each node in turn • Greedily tries adding edges from previous nodes to current node • Moves to next node when current node can’t be optimized further Pictures from Wikipedia and http://nltk.googlecode.com/svn/trunk/doc/book/ch06.html K2 Algorithm • Some tricks – Use Naïve Bayes classifier as a starting point. – Ensure that every node is in the Marcov blanket of the class node. (Marcov blanket: parents, children, and children’s parents) Naïve Bayesian Classifier Marcov blanket Other Algorithms • Extended K2 – sophisticated but slow – Do not order the nodes. – Greedily add or delete edges between arbitrary pairs of nodes. • Tree Augmented Naïve Bayes (TAN) Pictures from http://www.usenix.org/events/osdi04/tech/full_papers /cohen/cohen_html/index.html Other Algorithms • Tree Augmented Naïve Bayes (TAN) – Augment a tree to a Naïve Bayes classifier. – When the class node and its outgoing edges are eliminated, the remaining edges should form a Naïve Bayes classifier tree. Tree Other Algorithms • Tree Augmented Naïve Bayes (TAN) – MST of the network will be a clue for maximizing likelihood. Conditional Likelihood • What we actually need to know is the conditional likelihood, which is the conditional probability of the class given the other attributes. • However, what we’ve tried to maximize is, in fact, just the likelihood. O X Conditional Likelihood • Computing the conditional likelihood for a given network and dataset is straightforward. • This is what logistic regression does. Data Structures for Fast Learning • Learning Bayesian networks involves a lot of counting. • For each network structure to be searched, the data must be scanned to get the conditional probability tables. (Since the ‘given term’ of the table of a certain node changes frequently, we should rescan the data in order to get the brand new conditional probabilities many times.) Data Structures for Fast Learning • Use a general hash tables. – Assuming that there are 5 attributes, 2 with 3 values and 3 with 2 values. – There’re 4*4*3*3*3=432 possible categories. – This calculation includes cases of missing values. (i.e. null) – This can cause memory problems. Data Structures for Fast Learning • AD (all-dimensions) tree – Using a general hash table, there will be 3*3*3=27 categories, even though only 8 categories are actually used. Data Structures for Fast Learning • AD (all-dimensions) tree Only 8 categories are required, compared to 27. Data Structures for Fast Learning • AD (all-dimensions) tree - construction – Assume each attribute in the data has been assigned an index. – Then, expand node for attribute i with the values of all attributes j > i – Two important restrictions: • Most populous expansion for each attribute is omitted (breaking ties arbitrarily) • Expansions with counts that are zero are also omitted – The root node is given index zero Data Structures for Fast Learning • AD (all-dimensions) tree Data Structures for Fast Learning • AD (all-dimensions) tree Q. # of (humidity=normal, windy=true, play=no)? Data Structures for Fast Learning • AD (all-dimensions) tree Q. # of (humidity=normal, windy=false, play=no)? ? Data Structures for Fast Learning • AD (all-dimensions) tree Q. # of (humidity=normal, windy=false, play=no)? #(humidity=normal, play=no) – #(humidity=normal, windy=true, play=no) = 1-1=0 Data Structures for Fast Learning • AD tree only pay off if the data contains many thousands of instances. Pictures from http://news.ninemsn.com.au/article.aspx?id=805150 Questions and Answers • Any question?