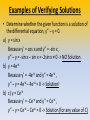Download 5.7 Differential Equations - Part 2

Warm-up
Solve
= k(y – 80) This represents Newton’s Law of Cooling,
where y is the core temperature of an
object and 80 is the ambient temperature
in Fahrenheit degrees.
It’s as easy as 1-2-3!
1) Start by separating variables.
2) Integrate both sides.
3) Solve for dy/dx.
Homework Review
• Anticipated Problem (P.368 #74):
When an object is removed from a furnace, its core
temperature is 1500 deg. F. The ambient temperature is
80 deg. F. In one hour the core cools to 1120 deg. F.
What is the core temperature after 5 hours?
Differential Equations – Part 2
Separation of Variables
Text – Section 5.7
Verifying Solutions
• In the last class, we learned that the general
solution of a differential equation could be made
particular by using initial conditions to solve for
any unknown constants.
• You can also verify that a solution, whether
general or particular, satisfies a differential
equation by plugging the solution into the
original equation. Note: When we plug a
solution, we must plug for all occurrences of y
and its derivatives in the original equation.
Examples of Verifying Solutions
• Determine whether the given function is a solution of
the differential equation, y” – y = 0.
a) y = sin x
Because y’ = cos x and y” = -sin x ,
y” – y = -sin x – sin x = -2sin x ≠ 0 -> NO Solution.
b) y = 4e-x
Because y’ = -4e-x and y” = 4e-x ,
y” – y = 4e-x – 4e-x = 0 -> Solution!
b) c) y = Ce-x
Because y’ = -Ce-x and y” = Ce-x ,
y” – y = Ce-x – Ce-x = 0 -> Solution (for any value of C)
Your Turn!
• Determine whether the given function is a
solution of the differential equation,
xy’ – 2y = x3ex
a) y = x2
b) y = x2(2 + ex)
Solving a Differential Equation and
Finding a Particular Solution
• Solve the equation, xy’ – 3y = 0.
• Find the particular solution, if y = 2, when x = -3.
Solving a Differential Equation and
Finding a Particular Solution
• Solve the equation, xy dx +
(y2 – 1) dy = 0
• Find the particular solution, if y(0) = 1.
Finding a Particular Solution Curve
• Find the equation of the curve that passes
through the point (1,3) and has a slope of y/x2 at
the point (x,y).
Applications
• #1 - The rate of change of the number of coyotes N(t) in
a population is directly proportional to 650 – N(t),
where t is the time in years. When t = 2, the population
has increased to 500. Find the population when t = 3.
Applications
• #2 – Describe the orthogonal trajectories for the family
of curves given by y = C/x for C ≠ 0.
– > xy = C
– > Implicit differentiation: xy’ + y = 0
–>
= - , slope of given family
– > What is the slope of the orthogonal family?