* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download File
Eigenvalues and eigenvectors wikipedia , lookup
Linear algebra wikipedia , lookup
System of polynomial equations wikipedia , lookup
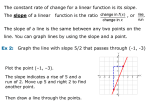
Cubic function wikipedia , lookup
Quadratic equation wikipedia , lookup
Quartic function wikipedia , lookup
History of algebra wikipedia , lookup
Signal-flow graph wikipedia , lookup
Elementary algebra wikipedia , lookup
Objectives ► The Slope of a Line ► Point-Slope Form of the Equation of a Line ► Slope-Intercept Form of the Equation of a Line ► Vertical and Horizontal Lines 1 Objectives ► General Equation of a Line ► Parallel and Perpendicular Lines ► Modeling with Linear Equations: Slope as Rate of Change 2 The Slope of a Line The slope of a line is the ratio of rise to run: If a line lies in a coordinate plane, then the run is the change in the x-coordinate and the rise is the corresponding change in the y-coordinate between any two points on the line (see Figure 2). Figure 2 3 The Slope of a Line This gives us the following definition of slope. The slope is independent of which two points are chosen on the line. 4 The Slope of a Line We can see that this is true from the similar triangles in Figure 3: Figure 3 5 Example 1 – Finding the Slope of a Line Through Two Points Find the slope of the line that passes through the points P(2, 1) and Q(8, 5). Solution: Since any two different points determine a line, only one line passes through these two points. From the definition the slope is . This says that for every 3 units we move to the right, the line rises 2 units. 6 Example 1 – Solution cont’d The line is drawn in Figure 5. Figure 5 7 Point-Slope Form of the Equation of a Line 8 Example 2 – Finding the Equation of a Line with Given Point and Slope (a) Find an equation of the line through (1, –3) with slope (b) Sketch the line. Solution: (a) Using the point-slope form with m = x1 = 1, and y1 = –3, we obtain an equation of the line as y+3= (x – 1) 2y + 6 = –x + 1 x + 2y + 5 = 0 Slope m = point (1, –3) Multiply by 2 Rearrange 9 Example 2 – Solution cont’d (b) The fact that the slope is tells us that when we move to the right 2 units, the line drops 1 unit. This enables us to sketch the line in Figure 7. Figure 7 10 Slope-Intercept Form of the Equation of a Line Suppose a nonvertical line has slope m and y-intercept b (see Figure 8). Figure 8 This means that the line intersects the y-axis at the point (0, b), so the point-slope form of the equation of the line, with x = 0 and y = b, becomes y – b = m(x – 0) 11 Slope-Intercept Form of the Equation of a Line This simplifies to y = mx + b, which is called the slope-intercept form of the equation of a line. 12 Example 4 – Lines in Slope-Intercept Form (a) Find the equation of the line with slope 3 and y-intercept –2. (b) Find the slope and y-intercept of the line 3y – 2x = 1. Solution: (a) Since m = 3 and b = –2, from the slope-intercept form of the equation of a line we get y = 3x – 2 13 Example 4 – Solution cont’d (b) We first write the equation in the form y = mx + b: 3y – 2x = 1 3y = 2x + 1 Add 2x Divide by 3 From the slope-intercept form of the equation of a line, we see that the slope is m = and the y-intercept is b= 14 Vertical and Horizontal Lines 15 Example 5 – Vertical and Horizontal Lines (a) An equation for the vertical line through (3, 5) is x = 3. (b) The graph of the equation x = 3 is a vertical line with x-intercept 3. (c) An equation for the horizontal line through (8, –2) is y = –2. (d) The graph of the equation y = –2 is a horizontal line with y-intercept –2. 16 Example 5 – Vertical and Horizontal Lines The lines are graphed in Figure 10. Figure 10 17 General Equation of a Line We have proved the following. 18 Example 6 – Graphing a Linear Equation Sketch the graph of the equation 2x – 3y – 12 = 0. Solution 1: Since the equation is linear, its graph is a line. To draw the graph, it is enough to find any two points on the line. The intercepts are the easiest points to find. x-intercept: Substitute y = 0, to get 2x – 12 = 0, so x = 6 y-intercept: Substitute x = 0, to get –3y – 12 = 0, so y = –4 19 Example 6 – Solution cont’d With these points we can sketch the graph in Figure 11. Figure 11 Solution 2: We write the equation in slope-intercept form: 2x – 3y – 12 = 0 2x – 3y = 12 Add 12 20 Example 6 – Solution –3y = –2x + 12 y= x–4 cont’d Subtract 2x Divide by –3 This equation is in the form y = mx + b, so the slope is m = and the y-intercept is b = –4. 21 Example 6 – Solution cont’d To sketch the graph, we plot the y-intercept and then move 3 units to the right and 2 units up as shown in Figure 12. Figure 12 22 Parallel and Perpendicular Lines 23 Example 7 – Finding the Equation of a Line Parallel to a Given Line Find an equation of the line through the point (5, 2) that is parallel to the line 4x + 6y + 5 = 0. Solution: First we write the equation of the given line in slope-intercept form. 4x + 6y + 5 = 0 6y = –4x – 5 Subtract 4x + 5 Divide by 6 24 Example 7 – Solution cont’d So the line has slope m = Since the required line is parallel to the given line, it also has slope m = From the point-slope form of the equation of a line, we get y–2= (x – 5) 3y – 6 = –2x + 10 2x + 3y – 16 = 0 Slope m = point (5, 2) Multiply by 3 Rearrange Thus, the equation of the required line is 2x + 3y – 16 = 0. 25 Parallel and Perpendicular Lines 26 Modeling with Linear Equations: Slope as Rate of Change When a line is used to model the relationship between two quantities, the slope of the line is the rate of change of one quantity with respect to the other. For example, the graph in Figure 17(a) gives the amount of gas in a tank that is being filled. Tank filled at 2 gal/min Slope of line is 2 Figure 17(a) 27 Modeling with Linear Equations: Slope as Rate of Change The slope between the indicated points is The slope is the rate at which the tank is being filled, 2 gallons per minute. 28 Modeling with Linear Equations: Slope as Rate of Change In Figure 17(b) the tank is being drained at the rate of 0.03 gallon per minute, and the slope is –0.03. Tank drained at 0.03 gal/min Slope of line is –0.03 Figure 17(b) 29 Example 11 – Slope as Rate of Change A dam is built on a river to create a reservoir. The water level w in the reservoir is given by the equation w = 4.5t + 28 where t is the number of years since the dam was constructed and w is measured in feet. (a) Sketch a graph of this equation. (b) What do the slope and w-intercept of this graph represent? 30 Example 11 – Solution (a) This equation is linear, so its graph is a line. Since two points determine a line, we plot two points that lie on the graph and draw a line through them. When t = 0, then w = 4.5(0) + 28 = 28, so (0, 28) is on the line. When t = 2, then w = 4.5(2) + 28 = 37, so (2, 37) is on the line. 31 Example 11 – Solution cont’d The line that is determined by these points is shown in Figure 18. Figure 18 (b) The slope is m = 4.5; it represents the rate of change of water level with respect to time. This means that the water level increases 4.5 ft per year. The -intercept is 28 and occurs when t = 0, so it represents the water level when the dam was constructed. 32