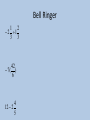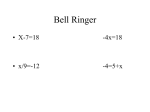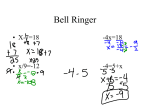Download Writing and Solving 1-Step Integer Equations

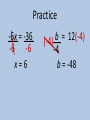
Bell Ringer
1 2
 2 1
3 3
42
 7( )
6
4
12  2
5
SOLVING 1-STEP
INTEGER EQUATIONS
Objective: To solve one-step integer
equations using addition,
subtraction, multiplication, and
division
Solve an Equation
• To find all values of a variable
that make an equation true
A one-step equation is as
straightforward as it sounds.
You will only need to perform
one step in order to solve the
equation.
Solving One-Step Equations
• Inverse Operation
• Operations that “undo” each other
• For example, addition “undoes”
subtraction and subtraction
“undoes” addition.
• Multiplication is the inverse of
division
Solving Equations Using Addition or
Subtraction:
• If a number has been added to the
variable, subtract that number from
both sides of the equation.
• If a number has been subtracted
from the variable, add that number
to both sides of the equation.
Example 1: Solve m + 7 = 11
m + 7 = 11
- 7 -7
m = 4
To undo the
addition of 7,
subtract 7 from
both sides of the
equal sign.
Check the solution.
Replace the
variable
with your
answer.
m + 7 = 11
(4) + 7 = 11
11 = 11 
Example 2: Solve -6 = m - 4
-6 = m - 4
+4
+4
-2 = m
To undo the
subtraction of 4,
add 4 to both sides
of the equal sign.
Check the solution.
Replace the
variable
with your
answer.
-6 = m - 4
-6 = (-2) - 4

-6 = -6
Practice
j - 3 = -12
+3 +3
j=-9
-4 + r = 26
+4
+4
r = 30
Solving Equations Using
Multiplication or Division
• If a variable has been multiplied by a
nonzero number, divide both sides
by that number.
• If a variable has been divided by a
number, multiply both sides by that
number.
Example 3: Solve 3y = 261
3y = 261
3
3
y = 87
To undo the
multiplication by 3,
divide 3 from both
sides of the equal
sign.
Check the solution.
Replace the
variable
with your
answer.
3y = 261
3(87) = 261
261 = 261 
Example 4:
Use the multiplication property of - 1
-1 is being
multiplied
to w
-w = 42
-1w = 42
-1 -1
w = -42
To undo the
multiplication of
-1 , divide both
sides by -1.
Check the solution.
Replace the
variable
with your
answer.
-w = 42
-(-42) = 42
42 = 42 
Practice
-6x = -36
-6
-6
x=6
b
=
12
(-4)
(-4)
-4
b = -48
Practice: Solve and Check
• 1. x-(-8)=4
• 3. x/7=-12
2. -5x=19
Practice: Solve and Check
• 4. x+7=-2
5. -4x=6
Practice: Solve and Check
• 6. 9=5+x
7. -5.1+x=-7.25