Download 9-1 Quadratic Equations & Functions

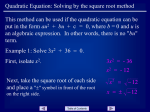
9-1 Quadratic Equations and Functions
Preview
Warm Up
California Standards
Lesson Presentation
9-1 Quadratic Equations and Functions
Warm Up
1. Evaluate x2 + 5x for x = 4 and x = –3.
36; –6
2. Generate ordered pairs for the function
y = x2 + 2 for x-values –2, –1, 0, 1, and 2.
x
–2
–1
0
1
2
y
6
3
2
3
6
9-1 Quadratic Equations and Functions
California
Standards
21.0 Students graph
quadratic functions and know that
their roots are the x-intercepts.
Also covered: 17.0
9-1 Quadratic Equations and Functions
Vocabulary
quadratic equation
quadratic function
parabola
minimum value
maximum value
vertex
9-1 Quadratic Equations and Functions
Solutions of the equation
y = x2 are shown in the graph.
Notice that the graph is not
linear. The equation y = x2 is a
quadratic equation. A
quadratic equation in two
variables can be written in the
form y = ax2 + bx + c, where a,
b, and c are real numbers and
a ≠ 0. The equation y = x2 can
be written as y = 1x2 + 0x + 0,
where a = 1, b = 0, and c = 0.
9-1 Quadratic Equations and Functions
Notice that the graph of
y = x2 represents a
function because each
domain value is paired with
exactly one range value. A
function represented by a
quadratic equation is a
quadratic function.
9-1 Quadratic Equations and Functions
Quadratic Equations and Their Graphs
For any quadratic equation in two variables
• all points on its graph are solutions to the
equation.
• all solutions to the equation appear on its
graph.
9-1 Quadratic Equations and Functions
Additional Example 1A: Determining Whether a
Point Is on a Graph
Without graphing, tell whether each point is on
the graph of
(4, 16)
Substitute (4, 16) into
?
=
?
16 = 8 + 8
16 = 16
Since (4, 16) is a solution of
(4, 16) is on the graph.
,
9-1 Quadratic Equations and Functions
Additional Example 1B: Determining Whether a
Point Is on a Graph
Without graphing, tell whether the function is on
the graph of
(–2, 10)
Substitute (–2, 10) into
?
=
?
10 = 2 + 8
10 = 10 
Since (–2, 10) is a solution of
(–2, 10) is on the graph.
,
9-1 Quadratic Equations and Functions
Additional Example 1C: Determining Whether a
Point Is on a Graph
Without graphing, tell whether each point is on
the graph of
(–4, 0)
Substitute (–4, 0) into
?
=
?
0= 8+ 8
0 ≠16 
Since (–4, 0) is not a solution of
(–4, 0) is not on the graph.
,
9-1 Quadratic Equations and Functions
Check It Out! Example 1a
Without graphing, tell whether the point is
on the graph of x2 + y = 2.
(1, 1)
Substitute (1, 1) into x2 + y = 2.
x2 + y = 2
?
12 + 1 = 2
?
1 + 1= 2
2 = 2
Since (1, 1) is a solution of x2 + y = 2, (1, 1) is
on the graph.
9-1 Quadratic Equations and Functions
Check It Out! Example 1b
Without graphing, tell whether the point is
on the graph of x2 + y = 2.
Substitute
into x2 + y = 2.
x2 + y = 2
Since
is not a solution
of x2 + y = 2,
on the graph.
is not
9-1 Quadratic Equations and Functions
Check It Out! Example 1c
Without graphing, tell whether the point is
on the graph of x2 + y = 2.
(–3.5, 10.5)
Substitute (–3.5, 10.5) into x2 + y = 2
x2 + y = 2
?
(–3.5)2 + 10.5 = 2
?
12.25 + 10.5 = 2
22.75 ≠ 2
Since (–3.5, 10.5) is not a solution of x2 + y =2,
(–3.5, 10.5) is not on the graph.
9-1 Quadratic Equations and Functions
The graph of a quadratic function
is a curve called a parabola. To
graph a quadratic function,
generate enough ordered pairs to
see the shape of the parabola.
Then connect the points with a
smooth curve.
9-1 Quadratic Equations and Functions
Additional Example 2A: Graphing Quadratic
Functions
Graph the quadratic function.
x
y
–2
4
3
1
3
–1
0
1
2
0
1
3
4
3
Make a table of
values. Choose
values of x and use
them to find values
of y.
Graph the points.
Then connect the
points with a
smooth curve.
9-1 Quadratic Equations and Functions
Additional Example 2B: Graphing Quadratic
Functions
Graph the quadratic function.
y = –4x2
x
y
–2
–16
–1
–4
0
0
1
–4
2
–16
Make a table of
values. Choose
values of x and
use them to find
values of y.
Graph the points.
Then connect the
points with a
smooth curve.
9-1 Quadratic Equations and Functions
Helpful Hint
When choosing values of x, be sure to choose
positive values, negative values, and 0.
9-1 Quadratic Equations and Functions
Check It Out! Example 2a
Graph each quadratic function.
y = x2 + 2
x
y
–2
6
–1
3
0
2
1
3
2
6
Make a table of values.
Choose values of x and
use them to find values
of y.
Graph the points. Then
connect the points with a
smooth curve.
9-1 Quadratic Equations and Functions
Check It Out! Example 2b
Graph the quadratic function.
y = –3x2 + 1
x
y
–2
–11
–1
–2
0
1
1
–2
2
–11
Make a table of values.
Choose values of x and
use them to find values
of y.
Graph the points. Then
connect the points with a
smooth curve.
9-1 Quadratic Equations and Functions
As shown in the graphs in Examples 2A and 2B,
some parabolas open upward and some open
downward. Notice that the only difference
between the two equations is the value of a.
When a quadratic function is written in the form
y = ax2 + bx + c, the value of a determines the
direction the parabola opens.
• A parabola opens upward when a > 0.
• A parabola opens downward when a < 0.
9-1 Quadratic Equations and Functions
Additional Example 3A: Identifying the Direction
of a Parabola
Tell whether the graph of the quadratic
function opens upward or downward. Explain.
Write the function in the form
y = ax2 + bx + c by solving for y.
Add
to both sides.
Identify the value of a.
Since a > 0, the parabola
opens upward.
9-1 Quadratic Equations and Functions
Additional Example 3B: Identifying the Direction
of a Parabola
Tell whether the graph of the quadratic
function opens upward or downward. Explain.
y = 5x – 3x2
y = –3x2 + 5x
Write the function in the
form y = ax2 + bx + c.
a = –3
Identify the value of a.
Since a < 0, the parabola opens downward.
9-1 Quadratic Equations and Functions
Check It Out! Example 3a
Tell whether the graph of each quadratic
function opens upward or downward. Explain.
f(x) = –4x2 – x + 1
f(x) = –4x2 – x + 1
a = –4
Identify the value of a.
Since a < 0 the parabola opens downward.
9-1 Quadratic Equations and Functions
Check It Out! Example 3b
Tell whether the graph of each quadratic
function opens upward or downward. Explain.
y – 5x2 = 2x – 6
y – 5x2 = 2x – 6
+ 5x2
+ 5x2
y = 5x2 + 2x – 6
a=5
Write the function in the form
y = ax2 + bx + c by solving
for y. Add 5x2 to both
sides.
Identify the value of a.
Since a > 0 the parabola opens upward.
9-1 Quadratic Equations and Functions
The minimum value of a function is the least
possible y-value for that function. The
maximum value of a function is the greatest
possible y-value for that function.
The highest or lowest point on a parabola is the
vertex. Therefore, the minimum or maximum
value of a quadratic function occurs at the
vertex.
9-1 Quadratic Equations and Functions
9-1 Quadratic Equations and Functions
Additional Example 4: Identifying the Vertex
and the Minimum or Maximum
Identify the vertex of each parabola. Then give
the minimum or maximum value of the function.
B.
A.
The vertex is (–3, 2), and
the minimum is 2.
The vertex is (2, 5), and
the maximum is 5.
9-1 Quadratic Equations and Functions
Check It Out! Example 4
Identify the vertex of each parabola. Then give
the minimum or maximum value of the function.
a.
b.
The vertex is (–2, 5) and
the maximum is 5.
The vertex is (3, –1), and
the minimum is –1.
9-1 Quadratic Equations and Functions
Unless a specific domain is given, the domain of a
quadratic function is all real numbers. One way to
find the range of a quadratic function is by looking
at its graph.
For the graph of y = x2 – 4x +
5, the range begins at the
minimum value of the function,
where y = 1. All y-values
greater than or equal to 1
appear somewhere on the
graph. So the range is y  1.
9-1 Quadratic Equations and Functions
Caution!
You may not be able to see the entire graph,
but that does not mean the graph stops.
Remember that the arrows indicate that the
graph continues.
9-1 Quadratic Equations and Functions
Additional Example 5: Finding Domain and Range
Find the domain and range.
Step 1 The graph opens
downward, so identify the
maximum.
The vertex is (–5, –3), so
the maximum is –3.
Step 2 Find the domain and
range.
D: all real numbers
R: y ≤ –3
9-1 Quadratic Equations and Functions
Check It Out! Example 5a
Find the domain and range.
Step 1 The graph opens
upward, so identify the
minimum.
The vertex is (–2, –4), so
the minimum is –4.
Step 2 Find the domain and
range.
D: all real numbers
R: y ≥ –4
9-1 Quadratic Equations and Functions
Check It Out! Example 5b
Find the domain and range.
Step 1 The graph opens
downward, so identify the
maximum.
The vertex is (2, 3), so the
maximum is 3.
Step 2 Find the domain and
range.
D: all real numbers
R: y ≤ 3
9-1 Quadratic Equations and Functions
Lesson Quiz: Part I
1. Without graphing, tell whether (3, 12) is on the
graph of y = 2x2 – 5. no
2. Graph y = 1.5x2.
9-1 Quadratic Equations and Functions
Lesson Quiz: Part II
Use the graph for Problems 3-5.
3. Identify the vertex.
(5, –4)
4. Does the function have a
minimum or maximum? What is
it? maximum; –4
5. Find the domain and range.
D: all real numbers;
R: y ≤ –4