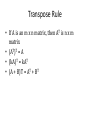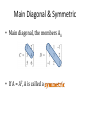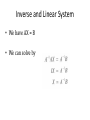Download Matrix

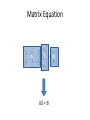
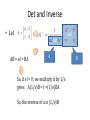
Matrix
REVIEW LAST LECTURE
Keyword
•
•
•
•
Parametric form
Augmented Matrix
Elementary Operation
Gaussian Elimination
• Row Echelon form
• Reduced Row Echelon form
• Leading 1’s
• Rank
• Homogeneous System
Goal of Elementary Operation
• To arrive at an easy system
Theorem 3
• Suppose a system of equation on
variables has a solution, if the rank of the
augmented matrix is
• the set of the solution involve exactly
parameters
The number
of leading
1’s
Homogeneous Equation
When b = 0
What is the
solution?
MATRIX REVIEW
Matrix Review
Square matrix
(number of row
equals number of
column
a13
c21
a22
A has 2 rows 3
columns
A is a 2 x 3
matrix
column matrix
Or
column vector
Matrix Review
• Scalar multiplication
• kA = [kaij]
Matrix Addition Rules
• A+B=B+A
• A + (B + C) = (A + B) + C
• There is an m x n matrix 0, such that 0 + A = A
for each A
• There is an m x n matrix, -A, such that A + (-A)
= 0 for each A
• k(A + B) = kA + kB
• (k+p)A = kA + pA
• (kp)A = k(pA)
Transpose
• Swap the index of rows and columns
• A = [aij]
• AT = [aji]
Transpose Rule
• If A is an m x n matrix, then AT is n x m
matrix
• (AT)T = A
• (kA)T = kAT
• (A + B)T = AT + BT
Main Diagonal & Symmetric
• Main diagonal, the members Aii
• If A = AT, A is called a
Example
• A = 2AT
• Solve for A
A = 2AT = 2[2AT]T = 2[a(AT)T] = 4A
0 = 3A
Hence A = 0
Dot Product
• Step in multiplication
• We need to compute
• 3*6 + -1 * 3 + 2 * 5
• The multiplication of (3 -1 2) and (6 3 5) is
called a dot product of row 1 and column 3
Identify Matrix
• A matrix whose main diagonal are 1’s and
0’s are elsewhere
• In most case, we assume that the identity
matrix is a square matrix
Multiplication Rules
• IA = A, BI = B
• A(BC) = (AB)C
• A(B + C) = AB + AC;
• A(B – C) = AB – AC
• (B + C)A = BA + CA;
• (B – C)A = BA – CA;
• k(AB) = (kA)B = A(kB) In most case
• (AB)T = BTAT
AB != BA
(no commutative!!)
Example
• When AB = BA? (when will they commutes?)
• (A – B)(A + B) = A2 – B2
MATRIX AND LINEAR EQUATION
Matrix and Linear Equation
Linear
equation
2x1
matrix
2 x 3 and
3x1
matrix
Matrix
equation
factoring
Matrix Equation
A
X
AX = B
B
Matrix Equation
Coefficient
matrix
Solution
AX = B
Constance
matrix
Associated homogeneous system
• Given a particular system AX = B
• There is a related system AX = 0
• Called associated homogeneous system
Solution of a linear system
• Let
• X1 be a solution to AX = B
• X0 be a solution to AX = 0
• X1 + X0 is also a solution of AX = B
• Why?
• A(X1 + X0) = AX1 + AX0 = B + 0 = B
Theorem 2
• Suppose X1 is a particular solution to the
system AX = B of linear equations.
• Then every solution X2 to AX = B has the
form
• X2 = X1 + X0
• For some solution X0 of the associated
homogeneous system AX = 0
Proof
• Suppose that X* is
solution to AX = B
• So, AX* = B
X1 is our
particular
• We write Xz = X* – X1
solution to AX = B
• Then AXz = A(X* + X1) = AX* + AX1 = B – B = 0
• Xz is the solution of AX = 0
• Hence, X* = Xz + X1 is the solution of AX = B
Implication of Theorem 2
• Given a particular system AX = B
• We can find all solutions by
• Find a particular solution to AX = B
• Reduce the problem into finding all solution to
AX = 0
Example
• Find all solution to
• Gaussian Elimination gives parametric form
• x = 4 + 2t
• y=2+t
• z=t
Basic Solution
Solve the homogeneous system AX = 0
 1 2 3 2
A   3 6 1 0
 2 4 4 2
Do the elimination
 1 2 3 2 0   1 2 0 1/ 5 0 





3
6
1
0
0

0
0
1

3
/
5
0

 

 2 4 4 2 0  0 0 0
0 0 
Basic Solution
 1 2 3 2 0   1 2 0 1/ 5 0 





3
6
1
0
0

0
0
1

3
/
5
0

 

 2 4 4 2 0  0 0 0
0 0 
x1 = 2s + (1/5), x2 = s, x3 = (3/5)t, x4 = t
1 

2s  t 

x
 1
 2  1/ 5 
5
x   s 
1   0 
  s t 
  sX  tX
X   2   
1
2

 x3 




3
0
3/ 5
t

  
  

5
 x4  

0  1 
 t 
Basic Solution
• A basic Solution is a solution to the
homogeneous system
Linear Combination
• The solution to the previous system is
sX1 + tX2
• Solutions in this form are called a linear
combination of X1 and X2
Linear Combination
• Consider the previous solution
 2  1/ 5 
1   0 

X  s t 
 0  3 / 5 
  

0
1
  

Linear Combination
• Consider the previous solution
 2 1/ 5 
 2
1 
1   0 
1 
0
  s    t /5 
X  s t 
 0  3 / 5
0
 3
  

 
 
0
1
0
  

 
5
We can let r =t / 5… Hence, it is also
another parametric form
but [1 0 3 5]T is a solution as well!!
Hence, a scalar multiple of a basic
solution is a basic solution as well
Relation to Rank
• A system AX = 0
• Having n variable and m equation (A is m x n
matrix)
• Suppose the rank of A is r
• Then there are n – r parameter (from theorem 3
of the last slide)
• We will have exactly n – r basic solutions
• Every solution is a linear combination of
these basic solutions
BLOCK MULTIPLICATION
Multiplication by Block
Block Multiplication
Compatibility
• Block multiplication is possible when
partition is compatible.
• i.e., size of partitioning allows multiplication of
the block
Can we divide
here?
MATRIX INVERSE
Solving equation
• How to solve a scalar equation
• ax = b
• Multiply both side by 1/a
ax/a = b/a
x = b/a
We need multiplicative
inverse
Matrix Inverse
• A matrix B is an inverse of a matrix A
• If and only if
is written as
and
Example
• Find the inverse of
• Let
• If B is the inverse, we have AB = I
Cannot
be I
Existence of an Inverse
• From the previous example
• There is a matrix having no inverse!!!
• Zero matrix cannot have an inverse
Non-Square matrix
•
•
•
•
What should be an inverse of non-square?
Let A is m x n matrix
What should be A-1?
We can have B = n x m such that
• AB = Im
and BA = In
• But this gives m = n
• If m < n, there exists a basic solution X (a 1 x n
matrix) for AX = 0
• So X = InX = (BA)X = B(AX) = B(0) = 0  contradict
 1 2 3 2
A   3 6 1 0
 2 4 4 2
Non square matrix has no inverse
Theorem 2.3.1
• If B and C are both inverse of A, then B = C
• If we have inverse, it must be unique.
Proof
• Since B and C are inverses
• CA = I = AB
• Hence
• B = IB = (CA)B = C(AB) = CI = C
Inverse
• For A
• A-1 is unique
• A-1 is square
First introduction to Det of 2 x 2 matrix
• Det  determinant
• Det of
• is (ad – bc)
Adjugate of 2 x 2
Adjugate of B
Det and Inverse
• Let
det
AB = eI = BA
e
So, if e != 0, we multiply it by 1/e
gives A(1/e)B = I =(1/e)BA
So, the inverse of a is (1/e)B
adj
B
Determinant
• Det exists before matrix
• Det is used to determine whether a linear
system has a solution
Inverse and Linear System
• We have AX = B
• We can solve by
Inversion Method
• A method to determine the inverse of A
based on solving linear equation system
• We have A = 2 x 2 matrix
• We need to find A-1
• We write the inverse as
Inversion Method
• We have AA-1 = I
• Gives
• Each are a system
• A is the coefficiency matrix
Solving A
• Find the equivalent systems in a reduced
row echelon form
• Gives
• This can be done by elementary operation
• In fact, we do this at the same time for both
equation
Inversion Method
• A short hand form [A I] [I A-1]
Double
matrix
Matrix Inversion Algorithm
• If A is a square matrix
• There exists a sequence of elementary row
operation that carry A to the identity matrix of
the same size.
• This same series carries I to A-1
Conclusion
• Matrix
• Det
• Inverse