Download Dia 1 - van der Veld

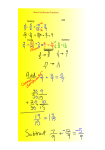
Multivariate Statistics
Matrix Algebra II
W. M. van der Veld
University of Amsterdam
Overview
• The determinant of a matrix
• The matrix inverse
• System of equations
The determinant of a matrix
• The determinant of a matrix is a scalar and is denoted as |A|
or det(A). Det(A) only exists when A is a square matrix.
• It has very important mathematical properties, but it is very
difficult to provide a substantive definition.
• The determinant is necessary to compute the inverse of a
matrix (A-1).
– The inverse of a matrix is needed for solving systems of linear equations;
multivariate statistics often comes down to this.
– When the determinant is zero, there exists no solution to a system of
linear equations.
• Let’s see how the value of the determinant is found.
The determinant of a matrix
• How to do it? The most simple case, a 2 by 2 matrix .
• Det(A)=|A|=?
Cofactors
 1 3
A  

0 4
1 3
Det ( A )  A 
 1* 4  3 * 0  4
0 4
 
 
The determinant of a matrix
• One step further, a 3 by 3 matrix.
• Det(A)=|A|=?
1  2  2


A  5 1
3 
8 0

4


  
  
  
1 3
5 3
A  1*
 2 *
0 4
8 4
Cofactor
5 1
 2*

8 0
 1(1 4  3  0 )  2(5  4  3  8 )  2(5  0  1 8 ) 
 (4  0)  ( 40  48)  (0  16)  12
The determinant of a matrix
• You should have noted that for matrices larger than first order,
computation of the determinant is a recursive process. This
process stops each time a 1 by 1 determinant is encountered,
and involves multiplication by the cofactors.
The determinant of a matrix
• Let A be a matrix of order n x n. If we omit one or more rows
or columns from A, we obtain a matrix of smaller order, called
a minor of the matrix.
• Similarly, we have minors of a determinant, and in particular,
if we omit from the determinant the ith row and the jth column,
the resulting minor will be square and its determinant will be
symbolized |Mij|. This determinant is called a cofactor (cij) if
we give it a sign equal to (-1)i+j, so that: cij = (-1)i+j |Mij|.
Using this notation we can write a formula for the expansion of
a determinant of order n:
n
A  ai1ci1  ai 2ci 2    aincin  aigcig In this version the
determinant is
g 1
expanded according
to it’s ith row.

The determinant of a matrix
• The following rules are important for determinants, and can
help you sometimes to simplify calculations:
– The determinant of A has the same value as the determinant of A’.
– The value of the determinant changes sign if one row (column) is
interchanged with another row (column).
– If a determinant has two equal rows (columns), its value is zero.
– If a determinant has two rows (columns) with proportional elements,
its value is zero.
– If all elements in a row (column) are multiplied by a constant, the
value of the determinant is multiplied by that constant.
– If a determinant has a row (column) in which all elements are zero,
the value of the determinant is zero.
– The value of the determinant remains unchanged if one row
(column) is added to or subtracted form another row (column).
Moreover, if a row (column) is multiplied by a constant and then
added to or subtracted from another row (column) the value remains
unchanged.
The determinant of a matrix
• What is the determinant of:
 2 4 8


A   1 2 3
 3 2 1


 1 0
B  

 0 1
1 4 
 5 10 
C  
 D  

 3 12 
12 24 
The matrix inverse
• Let A be a square matrix. If we can find a matrix B of the
same order as A such that AB=BA=I, then B is said to be the
inverse of A and is symbolized A-1. A-1, if exists, can be found
as follows.
• Let C be the matrix of cofactors of A (i.e., cij is the cofactor
obtained from the minor |Mij|); then
A 1  C / A
• Where C’ is the transpose of C (or if one prefers, C’ is the
matrix of cofactors of A’). It is immediately seen that the
inverse is undefined if A is not square (since then there is no
determinant |A|), and also if |A| is equal to zero.
The matrix inverse
• Illustration that AA-1 = A-1A = I.
1 4 
A  

3 2
  .2
A  
 .3
1
.4 

- .1 
1 4   0.2 0.4 
AA  

 
 3 2  0.3  0.1
1
 1( 0.2)  4(0.3) 1(0.4)  4( 0.1) 
AA  
 
 3( 0.2)  2(0.3) 3(0.4)  2( 0.1) 
1
 ( 0.2  1.2) (0.4  0.4)   1 0 
AA  
  
  I
 ( 0.6  0.6) (1.2  0.2)   0 1 
1
The matrix inverse
• How did I get A-1?
1 4 
A  

3
2


A
A
Compute determinant
1 4
 2  12  10
3 2
2  
C  





 2  4
C  


3
1


 
 
Now Compute C
 2  3
C  





 2  3
C  


4



Calculate A-1
 2  4



3
1
    0.2 0.4 
A 1  C  / A  
 0.3  0.1
 10


 2  3
C  


4
1


C transpose => C’
The matrix inverse
•
Another way to calculate A-1. This way introduces you to solving systems
of equations.
1 4 
A  

3 2
1
1
AA  
3
1 4  x11 x12  1 0 
  
AA  I  


x
x
3
2
0
1

 21 22  

4  x11 x12   1x11  4 x21 1x12  4 x22   1 0 




2  x21 x22   3x11  2 x21 3x12  2 x22   0 1 
1
1x11  4 x21  1
x11  1  0.2
5
3x11  2 x21  0  2;
 5x11  0 x21  1 
1x11  4 x21  1  3;
3x11  2 x21  0
0 x11  10 x21  3 
x21   3
 10
x12   2
1x12  4 x22
3x12  2 x22
5
 0.4  5x12  0 x22
1x12  4 x22
3x12  2 x22
 0.3
x22  1
  .2
A1  
 .3
1x11  4 x21
3x11  2 x21
1x12  4 x22
3x12  2 x22
 10
.4 

- .1 
 0.1
0 x12  10 x22




1
0
0
1
0
 1  2;
 2 
 0  3;
1
1 
The matrix inverse
• Rules for algebra with inverse matrices:
– AA-1 = A-1A = I
– (AB)-1 = B-1A-1
– (ABC)-1 = C-1B-1A-1
• Proof that (AB)-1 = B-1A-1.
System of equations
• In the introduction I already mentioned that the basic linear
equation y=bx will be very important for multivariate
methods.
• Here we will discuss how to solve systems of such linear
equations.
System of equations
• Illustration. Suppose we have the following set of equations:
-3=1x1+4x2
1=3x1+2x2
• The basic way to think about this problem set is finding the
intersection, i.e. for which unknowns are the equations
satisfied.
• This can be solved in a simple way (old style).
 3  1x1  4 x2
 1  3x1  2 x2
 5  5 x1 
* 2, add
x1  1
etc.  x2  ?
• The solution is basically the intersection of the lines
represented by the equation.
• You won’t be surprised that there is a more general way to
solve systems of linear equations, using matrix algebra.
System of equations
• Solution for m equations with n unknowns: m=n.
a12  a1n  x1 
 k1   a11
  
 
 k2   a21 a22  a2 n  x2 
k  Ax
   











k 
 
a



a

a
x
m2
mn  n 
 n   m1
• What to do? Normally you divide by A so that you obtain a
solution for x (give example: 15=3x).
• Matrix division is defined as multiplication by the inverse, so:
if
k  Ax  A 1k  A 1Ax  A 1k  Ix 
1
A kx
System of equations
• Example. Suppose we have the following set of equations:
-3=1x1+4x2
1=3x1+2x2
• We already solved this one, resulting in x1=1 and x2=-1.
• The set of equations can be written as a matrix operation.
  3  1

 1 

3

 
4  x1 







2  x2 
k  Ax
System of equations
• Thus, we have to find the inverse of: A => A-1 = C’/|A|
1
A
3

4



2
3
 22 3
C
 4 
 1
 


  
• We have to take the transpose of C
 4
 2
C  

 3

1


System of equations
• We have to divide by |A|.
1
A 
3
4
 (1  2)  (4  3)  10
2
• Thus the inverse matrix is.
A
1
1  2


 10 
 3
 4

1 

System of equations
• Thus a solution for:
-3=1x1+4x2
1=3x1+2x2 is found via
k  Ax
  3  1

 1 

3

 
A 1k  x
1  2

 10 
 3
 4   3  x1 











1  1   x2 
1  (2  3)  ( 4 1)   x1 







 10  ( 3  3)  (1 1)   x2 

1   10   1   x1 











 10  10    1  x2 

4  x1 







2  x2 
System of equations
Exercise, solve:
x1 + 2x2 = 0
3x1 + 7x2 = 1
1 2
A  

3 7
A-1Ax = Ix = x = A-1k
 0
k   
1
 7  2  0  0  2   2
A k  
    
     x
  3 1  1  0  1  1 
1
• So if Ax = k solve via x = A-1k.
• .... But it is not always so simple …
System of equations
• Sometimes, the requirement that m=n seems to be fulfilled,
so that there should exist a solution.
• But consider the following cases.
 8  2

16 

4
  
1  x1 
(Row 2 = 2 x Row 1)






2  x2 
1

1
2

1
2
3
1

2  (Row 3 = Row 1 + Row 2)
3

4

1
4

2
4
6
6

5  (Column 3 = Column 1 + Column 2), etc.
10 

System of equations
• These situations are called linear dependence:
– Given vectors: x1, x2,…, xn-1
– Another vector xn is linearly dependent if there exists
constants α1, α2,…, αn-1 such that:
xn= α1x1+α2x2+ …+αn-1xn-1
• Otherwise the vector xn is linearly independent.
• In case of linear dependence; |A|= 0.
• And then the inverse is not defined: A-1=C’/|A|.
• And when the inverse is not defined we cannot find a solution
via: A-1k=x.
System of equations
• Generally a unique solution exists only if m=n, and |A|≠0
• When are there ‘problems’?
– If m<n there are many solutions, the problem is underdetermined.
8x1+10x2+14x3=9
4x1+12x2+16x3=10
– if m>n there are no solutions, the problem is overdetermined.
8x1+10x2=9
4x1+12x2=10
4x1+10x2=2
System of equations
• Using the idea of linear dependency, the rank of a matrix can
be introduced.
• rank(A) = number of linearly independent rows or columns.
• Given an mxn matrix, with m ≥ n, then if
– |A| ≠ 0  rank(A) = n  full rank, solvable
– |A| = 0  rank(A) < n  rank deficient
• We will get back to the issue of rank.
Overdetermined Systems
• Find Ax “closest” to k
• Least-squares distance measure
Φ  ( Ax  k )( Ax  k )
• Minimization problem:
• Normal equations: (A’A)x = A’k
• Solution: x = (A’A)-1A’k
– A’A must be nonsingular; i.e. |A’A|≠0
– (A’A)-1A’ is called the left inverse matrix
Underdetermined Systems
• Find “smallest” x that satisfies equations
• Minimum norm objective
1
Φ  xx
2
• Constrained minimization problem:
• Solution: x = A’(AA’)-1k
– AA’ must be nonsingular
– A’(AA’)-1 is called the right inverse
min Φ
x
subject to : Ax  k