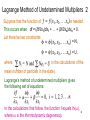Download Part IV

Photon Statistics 1
• A single photon in the state r has energy r = ħωr.
• The number of photons in any state r may vary from 0 to .
• The total energy of blackbody radiation is ER = ∑r nrr ,
where nr is the number of photons in the r’th state, so that
Zph(T, V) = ∑R exp (–ER).
• The state R of the complete system may be represented by
a set of occupation numbers (n1, n2, … nr, …).
• We show that ln Zph(T, V) = – ∑r ln [1 – exp(–εr)],
• and <nr> = – (1/) ∂(lnZph)/∂εr,
• which leads to
n(ω) = 1/(e
βħω
– 1).
1
Photon Statistics 2
2
Photon Statistics 3
This equation shows how to determine the mean number of
systems of energy εr.
3
Photon Statistics 4
For a continuous EM (photon) distribution, (ω) = ħω,
so that
n(ω) = 1/(e
βħω
– 1).
4
Density of States 1
• For a particle in a cube of side L, the wavefunction Ψ is zero at
the walls, so that
Ψ(n1,n2,n3) = sink1x sink2y sink3z,
where ki = niπ/L (i = 1,2,3), and each k-state is characterized
by the set of positive integers (n1, n2, n3).
• Neighboring states are separated by Δki = π/L , so that the
volume per state in k-space is (π/L)3 = π3/V.
In this 2-dimensional figure,
each point represents an
allowed k-state, associated
with an area in k-space of
(π/L)2.
5
Density of States 2
• The volume of a spherical shell of radius k is 4πk2dk, which
would contain 4πk2dk/(π3/V) = 4V k2dk/π2, where (π3/V) is the
volume in k-space associated with each state (n1, n2, n3).
• However, since only positive values of ni represent physical
situations, the number of k-states in range k to k + dk is (1/8)th
of that for the total shell; i.e. g’(k)dk = Vk2dk/(2π2).
6
Density of States 3
• In dealing with g’(k)dk = Vk2dk/(2π2), we transform from the
magnitude of the wave vector k to the angular frequency ; i.e.
g()d = g’(k)dk = g’(k)(dk/d)d.
• Since c = /k, g’(k) = Vk2/(2π2) = V2/(2π2c2), and dk/d = 1/c,
g()d = V2/(2π2c3) d.
• Thus, the number of photons in the range  to  + d equals
the number of photon states in that range g()d
times
the occupation of each state n(ω) = 1/(e βħω – 1).
• Thus, the energy density u(ω) is given by
u(ω)dω = (1/V) ħω n(ω) g(ω) dω.
Planck’s Radiation Law
• The, the energy density u(ω) is given by
u(ω)dω = (1/V) ħω n(ω) g(ω) dω.
• Inserting the values
g(ω) dω = V ω2 dω/π2c3 , n(ω) = 1/(eħω – 1) ,
we obtain
u(ω,) = ħω3 dω / π2c3(eħω – 1) .
• This is Planck’s radiation law, which on integration over all
frequencies gives the Stefan-Boltzmann law
u(T) = aT4,
where a = π2k4/15 ħ3c3 .
Note: letting x = ħ, u(,x)dω = (4π2c3ħ3)–1∫x3dx/(ex – 1).
8
Finding the Grand Partition Function ZG
9
Occupation Numbers 1
10
Occupation Numbers 2
11
Bose Einstein and Fermi-Dirac Statistics
• The symmetry requirements placed on a system of identical
quantum particles depends on their spin.
• Particles with integer spin (0, 1, 2,…) follow Bose-Einstein
statistics, in which the sign of the total wave function is
symmetrical with respect to the interchange of any two
particles; i.e.
Ψ( ∙ ∙ ∙ Qj ∙ ∙ ∙ Qk∙ ∙ ∙ ) = Ψ( ∙ ∙ ∙ Qk∙ ∙ ∙ Qi ∙ ∙ ∙ ).
• Particles with half-integer spin (1/2, 3/2, …) follow Fermi-Dirac
statistics, in which the sign of the total wave function is
antisymmetrical with respect to the interchange of any two
particles; i.e.
Ψ( ∙ ∙ ∙ Qj ∙ ∙ ∙ Qk∙ ∙ ∙ ) = – Ψ( ∙ ∙ ∙ Qk∙ ∙ ∙ Qi ∙ ∙ ∙ ).
Thus, two particles cannot be in the same state, since Ψ = 0,
12
when particles j and k are in the same state.
Two-Particle Systems
• Writing the wavefunction for particle j in state A as ψj(qA) etc.,
we have the following situations:
• Maxwell-Boltzmann statistics: Ψ = ψj(qA)ψk(qB).
• Bose-Einstein (BE) statistics: Ψ = ψj(qA)ψk(qB) + ψj(qB)ψk(qA).
In this case, the total wave function Ψ is antisymmetrical.
Examples of bosons are photons and composite particles,
such as H1 atoms or He4 nuclei.
• Fermi-Dirac (FD) statistics: Ψ = ψj(qA)ψk(qB) – ψj(qB)ψk(qA).
In this case, the total wave function Ψ is symmetrical.
Ψ = 0, if both particles are placed in the same state – the Pauli
exclusion principle.
Examples of bosons are electrons, protons, neutrons, and
composite particles, such as H2 atoms or He3 nuclei.
13
Grand Partition Function ZG
• To obtain the grand partition function ZG , we consider a
system in which the number of particles N can vary, which is in
contact with a heat reservoir.
• The system is a member of a grand canonical ensemble, in
which T, V and μ (the chemical potential) are constants.
• Assume that there are any number of particles in the system,
so that 0 ≤ N ≤ No → , and an energy sequence for each
value of N,
UN1 ≤ UN2 ≤ … ≤ UNr …
in which,
Vo = V + Vb, Uo = U + Ub, No = N + Nb,
where Vb etc. refer to the reservoir and Vo etc. to the total.14
Comparison of ZG with Z
Bath type
Heat bath
Heat and particle bath
Probability
pr = exp (– Er)/Z
pN,r = exp (μN – EN,r)/Z
Statistical Z = r=1 exp (– Er) ZG= N=0 r=1 exp (μN – EN,r)
parameter Partition function
Grand partition function
• The state N,r of the system may be written as a set of
particle occupation-numbers (n1, n2,…, nr, …), with
ni = (1/)[∂(lnzGi)/∂μ].
• Fermions (particles with half-integer spin): ni = 0 or 1.
• Bosons (particles with integer spin): ni = 0,1, 2,…… ∞.
15
Fermi-Dirac Statistics
ni is the mean no of spin-1/2 fermions in the i’th state.
All values of μ, positive or negative are allowable, since
ni always lies in the range 0 ≤ ni ≤ 1.
16
Bose-Einstein Statistics
ni is the mean no of bosons in the i’th state.
∑ni = N, the total number of particles in the system of like particles.
ni must be positive and finite, i  μ for all i.
For an ideal gas, i = p2/2m  min = 0, so that μ must be negative.
For a photon gas, μ = 0.
17
Density of States 4
• For a set of spin-zero bosons,
g’(k)dk = V k2dk /(2π2).
• For a set of spin-½ fermions,
g’(k)dk = 2V k2dk /(2π2),
since each set of quantum numbers (n1, n2, n3), has two
possible spin states.
• The number of states in the range  to  + d is given by
f()d = g’(k)dk = g’(k)(dk/d)d.
• Now
so that
 = p2/2m = (kħ)2/2m,
k = √(2m)/ħ ,
dk/d = (1/2ħ)(2m/)1/2.
18
Density of States 5
Bose-Einstein condensation (spin 0 system)
• The number of states in the range  to  + d is given by
f()d = g(k)dk = g(k)(dk/d)d,
with
g(k) = Vk2/(2π2),
k = √(2m)/ħ , dk/d = (1/2ħ)(2m/)1/2.
• Hence,
f()d = Vk2(dk/d)d/2π2 = V[4πm/ħ3](2m/)1/2d;
i.e.
f()d = (2πV/h3)(2m)3/21/2 d.
Free electron theory (spin ½ system)
f()d = (4πV/h3)(2m)3/21/2 d.
19
Density of States 6
• Suppose that for an N-particle system with continuous ε,
i.
the number of states in the range ε to ε + dε is f()d;
ii.
the mean number of particles of energy  is <n()>.
• The number of particles with energies in the range ε to ε + dε is
dN(ε) = <n()> f()d.
• Thus, the total no. of particles is given by N = ∫dN(ε), and the
total energy is given by U = ∫ε dN(ε) = ∫ε <n()> f()d, where
the integration limits are 0 and ∞.
• The values of <n()> for quantum systems are given by
<n()> = 1/{exp[β(ε – μ)] ± 1}.
• The distribution f()d is called the density of states.
20
Mean number of bosons or fermions
If there is a fixed number of particles N, ∑<n(ε)> = N
21
Classical limit
• Quantum statistics gives
<nr> = 1/{exp[β(εr – μ)] ± 1}.
• In the classical limit, the energy states r are infinitesimally
close, so that
<nr> → 0, <nr>–1 → ∞, exp[β(εr – μ)] » 1
and
<nr> → exp[β(μ – εr)] = exp(βμ). exp(– εr) ,
where z is the single-particle partition function.
• The single-particle Boltzmann distribution is
pr = <nr>/N = exp(– εr).z .
• Thus,
N = z exp(βμ).
22
Summary
• Consider N particles of an ideal quantum gas, with closely
spaced states, which may be taken as a continuum.
• Such is the case for the energy of a molecule of an ideal
monatomic gas ε = p2/2m.
• The number of states in the range ε to ε + dε is given by
f(ε) dε = C ε1/2 dε,
where C = (2πV/h3)(2m)3/2 for spin 0 bosons,
and (4πV/h3)(2m)3/2 for spin ½ fermions.
• The occupation numbers of each state are given by the BE and
FD distribution functions
<n(ε)> = 1/{exp[β(ε – μ)] – 1} and 1/{exp[β(ε – μ)] +1}
respectively.
The distribution of particles is given by dN(ε) = <n()> f()d.
LOW TEMPERATURE FD DISTRIBUTION
• As β → 0, exp[β(ε – μ)] behaves as follows:
• If ε < μ, exp[β(ε – μ)] → exp(-∞) = 0, so that <n(ε)> = 1;
if ε > μ, exp[β(ε – μ)] → exp(∞) = ∞, so that <n(ε)> = 0.
• Thus dN(ε) = f(ε)dε for ε < μ, and dN(ε) = 0 for ε > μ.
The Fermi energy F is defined as F ≡ μ(T → 0).
Free-Electron Theory: Fermi Energy 1
The Fermi energy F ≡ μ(T=0)
At T=0, the system is in the state of lowest energy, so that the N lowest
single-particle states are filled, giving a sharp cut-off in n() at T = TF.
At low non-zero temperatures, the occupancies are less than unity, and
states with energies greater than μ are partially occupied.
Electrons with energies close to μ are the ones primarily excited.
The Fermi temperature TF = F/k lies in the range 104 – 105 K for metals with
one conduction electron per atom.
25
Below room temperature, T/TF < 0.03, and μ ≈ F.
Free-Electron Theory: Heat capacity
Simplified calculation for T << TF
Assume that only those particles within an
energy kT of F can be excited and have
mean energies given by “equipartition”; i.e.
Neff  N(kT/F) = NT/TF.
Thus, U  Neff(3/2)kT = (3/2)NkT2/TF,
so that
CV = dU/dT  3NkT/TF.
In a better calculation, 4.9 replaces 3.
Thus, for a conductor at low temperatures,
with the Debye term included,
CV = AT3 + γT,
so that
CV/T = AT2 + γ.
26
Free-Electron Theory: Fermi Energy 2
The number of electrons with energies between  and  + d is given by
dN() = n() f() d, where n() = 1/{[exp( – μ)] + 1}, .
27
Free-Electron Theory: Calculation of <n>.
Now U = 0 n()f() d.
28
LOW TEMPERATURE B-E DISTRIBUTION
• The distribution of particles dN(ε) = <n()> f()d cannot work
for BE particles at low temperatures, since all the particles
enter the ground-state, while the theoretical result indicates
that the density of states [f(ε) = C ε1/2] is zero at ε = 0.
• The thermodynamic approach to Bose-Einstein
Condensation shows the strengths and weaknesses of the
statistical method:
mathematical expressions for the phenomena are obtained
quite simply, but a physical picture is totally lacking.
• The expression dN(ε) = <n()> f()d works down to a phase
transition, which occurs at the Bose or condensation
temperature TB, above which the total number of particles is
given by N = ∫ dN(ε).
• Below TB , appreciable numbers of particles are in the
ground state.
Bose-Einstein Condensation 1
• The number of particles with energies in the range ε to ε + dε is
dN(ε) = <n()> f()d,
with
<n()> = 1/{exp[β(ε – μ)] – 1}
and
f()d = (2πV/h3)(2m)3/21/2 d.
• Thus,
dN(ε) = (2πV/h3)(2m)3/21/2 d /{exp[β(ε – μ)] – 1},
and the total number of particles N is given by
N = (2πV/h3)(2m)3/2 ∫1/2 d /{exp[β(ε – μ)] – 1},
which is integrated from  = 0 to ∞.
30
Bose-Einstein Condensation 2
• Since the number of particles are fixed, with
N = (2πV/h3)(2m)3/2 ∫1/2 d /{exp[β(ε – μ)] – 1},
the integral
• ∫1/2 d /{exp[β(ε – μ)] – 1}
must be positive and independent of temperature.
• Since min= 0 for an ideal gas, the chemical potential μ ≤ 0, the
factor
exp(β |μ|) – 1 = exp(|μ|/kT) – 1,
must be constant, so that (|μ|/T) is independent of temperature.
• This can happen only down to the Bose Temperature TB, at
which μ becomes 0.
What happens below TB?
31
Bose-Einstein Condensation 3
• At the Bose (or condensation) temperature TB, μ ≈ 0, so that
N = (2πV/h3)(2m)3/2 ∫1/2 d /{exp(ε/kTB) – 1},
which yields on integration, TB = (h2/2πmk)(N/2.612V)2/3.
• The expression f()d = K1/2 d, with K = (2πV/h3)(2m)3/2,
indicates that for T > TB, the number of particles in the
ground state ( = 0) is negligible, since f() = K1/2 → 0.
Behavior of μ above TB.
Bose-Einstein Condensation 4
33
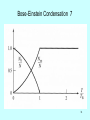
Bose-Einstein Condensation 5
For T >TB, the number of particles in the ground state (N) is zero.
34
Bose-Einstein Condensation 6
35
Bose-Einstein Condensation 7
36
Bose-Einstein Condensation 8
37
Bose-Einstein Condensation 9
Classical high-temperature value
38
Bose-Einstein Condensation 10
39
Appendix
Alternative Approach to Quantum Statistics
PHYS 4315
R. S. Rubins, Fall 2008
Lagrange Method of Undetermined Multipliers 1
Simple example
• How to find an extremum for a function f(x,y), subject to the
constraint φ(x,y) = constant.
• Suppose f(x,y) = x3 +y3, and φ(x,y) = xy = 4.
Method 1
Eliminating y, f(x,y) = x3 +(4/x)3, so that df/dx = 3x2 - 3(4/x)4
When df/dx = 0, x6 = 64,  x = 2, y = 2.
Method 2 (Lagrange method)
and
= α, so that
In this example, α is a Lagrange undermined multiplier.
41
Lagrange Method of Undetermined Multipliers 2
Suppose that the function of
is needed.
This occurs when df = (∂f/∂x1)dx1 + … + (∂f/∂xn)dxn = 0.
Let there be two constraints
= N,
= U,
where
in the calculations of the
mean number of particles in the state j.
Lagrange’s method of undetermined multipliers gives
the following set of equations:
In the calculations that follow, the function f equals ln(ω), 42
where ω is the thermodynamic degeneracy.
Alternate Fermi-Dirac Calculation 1
If the j’th state has degeneracy gj, and contains Nj particles,
Nj ≤ gj for all j, since the limit is one particle per state; e.g.
The number of ways of dividing N indistinguishable particles
into two groups is
In the Fermi-Dirac case,
.
43
Alternate Fermi-Dirac Calculation 2
The total no. of microstates is obtained by summing over all j; i.e.
Therefore,
Using Stirling’s theorem, ln N! ≈ N ln N – N, we obtain
44
Alternate Fermi-Dirac Calculation 3
Since the constraints are
,
we let φ(N1…Nj…) = N, and ψ(N1 …Nj…) = U, so that
,
where α and β are Lagrange multipliers.
Inserting the expression for ln ωFD and remembering that
we obtain
45
.
Alternate Fermi-Dirac Calculation 4
reduces to
Thus <nj> =
.
The constraint α has been replaced by μ/kT, where
μ is the chemical potential, and β by –1/kT.
46
Alternate Bose-Einstein Calculation 1
The j’th energy level has gj quantum states, and contains a
total of Nj identical particles, with up to Nj particles in each state.
All possible microstates can be obtained by rearranging (gj – 1)
partitions and Nj dots, in a diagram like that shown below.
The number of microscopes for a given Nj and gj is
.
47
Alternate Bose-Einstein Calculation 2
The total no. of microstates is obtained by summing over all j; i.e.
Therefore,
Using Stirling’s theorem, ln N! ≈ N ln N – N, we obtain
48
Alternate Bose-Einstein Calculation 3
Using the method of Lagrange multipliers as before,
where α and β are Lagrange multipliers.
Inserting the expression for ln ωFD, we obtain
hence
49
.
Alternate Bose-Einstein Calculation 4
reduces to
Thus <nj> =
.
The constraint α has been replaced by μ/kT, where
μ is the chemical potential, and β by –1/kT.
50