* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Concepts 1.1
Survey
Document related concepts
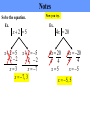
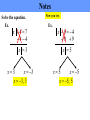
Transcript
Bell Work 11/4/14 Solve for the indicated variable. 1. 5a 2 7b for a 2. 3a 8 5 for a b Yesterday’s Homework 1. Any questions? 2. Please pass your homework to the front. • Make sure the correct heading is on your paper. • Is your NAME on your paper? • Make sure the homework is 100% complete. • Incomplete work will NOT be accepted. Heading 5/24/2017 2.7 Solving Absolute-Value Equations TSWBAT: solve equations that involve absolute value symbols. Students solve equations and inequalities involving absolute values. Notes • Absolute Value x = The distance the point is from zero. Ex. What is the absolute value of 2? 2 • ALWAYS positive. • NEVER negative. Find the absolute value. Ex. Ex. 7 7 How far is 2 from 0? What is 2 ? 2 2 2 Now you try. 9 9 Ex. 13 13 Ex. 79 79 Notes Find the absolute value. Ex. Ex. What two numbers x 5 x 9 are 5 away from zero! x 5 x 5 x 5, 5 x 9 x 9 x 9, 9 Now you try. Ex. x 1 x 1 x 1 x 1, 1 Ex. x 2 x No Solution Notes Solve the equation. Ex. x2 5 x 2 5 x 2 5 2 2 2 2 x 3 x 7 x 7, 3 Now you try. Ex. 4 x 20 4x 20 4 4 x 5 4 x 20 4 4 x 5 x 5, 5 Notes Solve the equation. Ex. 3x 9 6 Now you try. Ex. 2x 6 2 3x 9 6 3x 9 6 2x 6 2 2x 6 2 9 9 9 9 6 6 6 6 3x 3 3x 15 2x 8 2 x 4 3 3 3 3 2 2 2 2 x 1 x 5 x 2 x 4 x 5, 1 x 4, 2 Notes Solve the equation. Ex. x 47 4 4 x 3 x 3 x 3 x 3, 3 Now you try. Ex. x 9 4 9 9 x 5 x 5 x 5 x 5, 5 Notes Solve the equation. Ex. x 6 7 11 7 7 x6 4 x6 4 6 6 x 2 x 6 4 6 6 x 10 x 10, 2 Now you try. Ex. 3x 2 14 2 2 3x 12 3x 12 3 3 x4 3x 12 3 3 x 4 x 4, 4 Notes Solve the equation. Ex. 3 2 x 8 15 3 15 15 3 2 x 8 18 3 3 2x 8 6 2x 8 6 8 8 2x 14 2 2 x7 2x 8 6 8 8 2x 2 2 2 x 1 x 1, 7 Notes Now you try. Solve the equation. Ex. 2 3x 5 8 6 8 8 2 3x 5 14 2 2 3x 5 7 3x 5 7 5 5 3x 12 3 3 x4 3x 5 7 5 5 3x 2 3 3 x 23 2 x , 4 3 Summary value To solve equations involving absolute ______ bars first make sure that the absolute value bars are isolated to one side. Next _______ branch off into two ________ problems, one set to the original positive number and equations negative Finally solve both _________ one set to the ________. separately. Today’s Homework Rules for Homework 1. Pencil ONLY. 2. Must show all of your work. • NO WORK = NO CREDIT 3. Must attempt EVERY problem. 4. Always check your answers. Homework 2.7 Solve the equation. 1. x 7 2. x 3 3. x4 9 4. 7 x 21 5. 3x 12 6 6. 4x 8 4 7. x 5 11 8. x 4 3 2 9. 3x 6 2 11 10. 5 2 x 8 12 8 Ticket Out the Door Complete the Ticket Out the Door without talking!!!!! Talking = time after the bell! Put your NAME on the paper. When finished, turn your paper face DOWN. Solve the equation. 2x 8 4