Download Document

Chap. 4: Finite Fields
Jen-Chang Liu, 2005
Adapted from lecture slides by
Lawrie Brown
The next morning at daybreak, Star flew indoors,
seemingly keen for a lesson. I said, "Tap eight."
She did a brilliant exhibition, first tapping it in 4,
4, then giving me a hasty glance and doing it in
2, 2, 2, 2, before coming for her nut. It is
astonishing that Star learned to count up to 8
with no difficulty, and of her own accord
discovered that each number could be given
with various different divisions, this leaving no
doubt that she was consciously thinking each
number. In fact, she did mental arithmetic,
although unable, like humans, to name the
numbers. But she learned to recognize their
spoken names almost immediately and was able
to remember the sounds of the names. Star is
unique as a wild bird, who of her own free will
pursued the science of numbers with keen
interest and astonishing intelligence.
— Living with Birds, Len Howard
Introduction

Finite fields: increasing importance in
cryptography


AES, Elliptic Curve, IDEA, Public Key
Goal: mathematics for GF(2n)
Ciphertext: 2n
Plaintext: 2n
11010…0111
01100…0100
T(Plaintext, Key)
1. Arbitrary mapping => large transform table
2. Mathematical form, ex. Hill cipher
Outline






Group, rings, and fields
Modular arithmetic
Finite fields of the form GF(p), p is a prime
Euclid’s algorithm (find GCD)
Polynomial arithmetic
Finite fields of the form GF(2n)
Motivation for abstract math


Abstract math.: 數學物件的集合，運算方式
在一個數學物件的集合中，可操作的運算種
類？(+, - , x, /)
Group +,+,-,x Ring
+,-,x,/ Field
Group

Group: {G, •}








G: a set of elements
•: binary operation to each pair (a,b) in G
obeys:
Ex. Integers and +
closure: a•b is also in G
1+2=3
associative law: (a•b)•c = a•(b•c) (1+2)+3=1+(2+3)
has identity e:
e•a = a•e = a
3+0=0+3=3
has inverses a-1: a•a-1 = e
2+(-2)=0
if commutative

a•b = b•a
then forms an abelian group
Cyclic Group

Def: exponentiation as repeated
application of operator

example:
a3 = a•a•a

and let identity be:

cyclic group



e=a0
every element is a power of some fixed element
i.e. b = ak for some a and every b in group
a is said to be a generator of the group
EX. integers with addition: 1 as the generator
Ring





Ring: {R, +, x}
 R: a set of “numbers”
 +,x: two operations (addition & multiplication)
Ring obeys
set of even integers (pos, neg, and 0)
{R,+}: an abelian group
multiplication:
 has closure
 is associative: ax(bxc)=(axb)xc
 distributive over addition:
ax(b+c) = axb + axc
trivial
2x4 = 8
2x(4x6) = (2x4)x6
2x(4+6)=2x4+2x6
if multiplication operation is commutative, it forms
a commutative ring axb = bxa
Field


Field: {F, +, x}

F: a set of numbers

+,x: two operations (addition & multiplication)
Field obeys:



Ring
{F, +}: abelian group for addition
{F\0, x}: abelian group for multiplication (ignoring
0)


i.e. with multiplication inverse => division is possible
Ex. Real number, {Z, +, x} 不是，無乘法反元素
Field for n-bit block?
Ciphertext: 2n
Plaintext: 2n
11010…0111
01100…0100
+: addition
x: multiplication
?
Problems: 1. the set of plaintext (and ciphertext) is finite
2. how to define +,-,x,/ operations
Ex. 2-bit input
00
01
10
11
如何定義+,-,x,/ 運算？
Outline






Group, rings, and Fields
Modular arithmetic
Finite fields of the form GF(p)
Euclid’s algorithm (find GCD)
Polynomial arithmetic
Finite fields of the form GF(2n)
Modulo operator

modulo operator: a mod n to be the
remainder (>0) when a is divided by n
a  a / n  n  (a mod n)
, a and n are integers
Modulo operator (cont.)

Integers a and b are congruence modulo n
a ≡ b mod n



when divided by n, a & b have same remainder
eg. 100 ≡ 34 mod 11
b is called the residue of a: b= a mod n


integers can always write: a = qn + b
usually have 0 <= b <= n-1
-12 mod 7 = 2
Integers Modulo 7 Example
...
-21 -20 -19 -18 -17 -16 -15
-14 -13 -12 -11 -10 -9 -8
-7 -6 -5 -4 -3 -2 -1
0
1
2
3
4
5
6
7
8
9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31 32 33 34
...
congruence
Z7: residue class
modulo 7
Question:


(mod n) maps all integers into the set
Zn={0, 1, 2, …, n-1}
Can we perform arithmetic (+,-,x,/) with
this set?
Modular Arithmetic



We can do modular arithmetic with any set
of integers: Zn={0, 1, … , n-1}
Under normal arithmetic (+,-,x)
Properties:
1. [(a mod n)+(b mod n)] mod n = (a+b) mod n
2. [(a mod n)- (b mod n)] mod n = (a-b) mod n
3. [(a mod n)x (b mod n)] mod n = (axb) mod n
Modulo 8 Example: add
Find
Additive
inverse
=> group
Modulo 8 Example: multiply
Not all have
Multi. Inverse
 Not a
field
Does not
produce all
elements in
Z8
Modular Arithmetic (cont.)

Peculiarities compared with ordinary arith.

if (a+b)≡(a+c) mod n then b≡c mod n

Existence of (-a):
((-a)+a+b)≡((-a)+a+c) mod n

if (ab)≡(ac) mod n then b≡c mod n ?

Existence of (a-1) ?
((a-1) ab)≡((a-1) ac) mod n
Not always true, eg. n=8
Multiplicative inverse exists iff. a is relatively prime to n
Question

Do we have a finite field within Zn ?
Modulo 7 example: addition
Yes for
additive
inverse
Modulo 7 Example: multiply
 Yes for
multi. inverse
Question


Do we have a finite field within Zn ?
Galois field
 GF(p): ZP ,the modulo p is a prime number
 Under ordinary arithmetic
n
 GF(p ): Z n , p is a prime number
p
3
 2 does not form a field under normal
arithmetic
 Under polynomial arithmetic
Outline






Group, rings, and Fields
Modular arithmetic
Finite fields of the form GF(p)
Euclid’s algorithm (find GCD)
Polynomial arithmetic
Finite fields of the form GF(2n)
Galois Fields: GF(p)
Theorem: Zn={0,1,…,n-1} is a commutative
ring. Any integer aZn in has a multiplicative
inverse iff a is relatively prime to n
 In other words,
 If n is a prime number, then all nonzero
integers in Zn are relatively prime to n
=> all nonzero integers in Zn have multiplicative
inverses
=> Zn is a finite field
=> GF(p), p is a prime

Galois Fields: GF(p)


GF(p) is the set of integers {0,1, … , p-1}
with arithmetic operations modulo prime p
these form a finite field


since have multiplicative inverses
hence arithmetic is “well-behaved” and can
do addition, subtraction, multiplication, and
division without leaving the field GF(p)
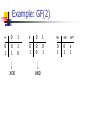
Example: GF(2)
+
0
1
x
0
1
w
-w
w-1
0
1
0
1
1
0
0
1
0
0
0
1
0
1
0
1
x
1
XOR
AND
Q: How to find the multiplicative
inverse?


For GF(7), it is easy to build a table
For GF(1759), how to find the multiplicative
inverse of 550?
Outline






Group, rings, and Fields
Modular arithmetic
Finite fields of the form GF(p)
Euclid’s algorithm (find GCD) and extended
Euclid’s algorithm (find multiplicative inverse)
Polynomial arithmetic
Finite fields of the form GF(2n)
Greatest Common Divisor (GCD)


a common problem in number theory
GCD (a,b) of a and b is the largest number
that divides evenly into both a and b


eg. GCD(60,24) = 12
GCD(.,.)=1: no common factors (except 1)
and hence numbers are relatively prime


eg. GCD(8,15) = 1
hence 8 & 15 are relatively prime
Euclid's GCD Algorithm

uses theorem that: (a>b>0)

GCD(a,b) = GCD(b, a mod b)
To prove: The set of common divisors of a and b
= The set of common divisors of a and (a mod b)
Example GCD(1970,1066)
1970 = 1 x 1066 + 904
1066 = 1 x 904 + 162
904 = 5 x 162 + 94
162 = 1 x 94 + 68
94 = 1 x 68 + 26
68 = 2 x 26 + 16
26 = 1 x 16 + 10
16 = 1 x 10 + 6
10 = 1 x 6 + 4
6 = 1 x 4 + 2
4 = 2 x 2 + 0
gcd(1066, 904)
gcd(904, 162)
gcd(162, 94)
gcd(94, 68)
gcd(68, 26)
gcd(26, 16)
gcd(16, 10)
gcd(10, 6)
gcd(6, 4)
gcd(4, 2)
gcd(2, 0)
Finding Inverses

can extend Euclid’s algorithm:
EXTENDED EUCLID(m, b)
1.(A1, A2, A3)=(1, 0, m);
(B1, B2, B3)=(0, 1, b)
2. if B3 = 0
return A3 = gcd(m, b); no inverse
3. if B3 = 1
return B3 = gcd(m, b); B2 = b–1 mod m
4. Q = A3 div B3
5. (T1, T2, T3)=(A1 – Q B1, A2 – Q B2, A3 – Q B3)
6. (A1, A2, A3)=(B1, B2, B3)
7. (B1, B2, B3)=(T1, T2, T3)
8. goto 2
Inverse of 550 in GF(1759)
B2=A2-Q*B2=0-3*1=-3
(商)
4
1
inverse
0
Recall: inverse matrix in Hill
cipher



9 4

Find inverse matrix for K  
5 7
Note that 26 is not a prime, not every
element in {0,1,2,…,25} has multiplicative
inverse
Inverse formula:
K
1
 7  4  1  7 22 
1

  


9  7  5  4   5 9  43  21 9 
Inverse of Hill cipher
Q
1
1
1
8
A3 B3
26 17
17
9
9
8
8
1
1
0
A2 B2
0
1
1
-1
-1
2
2
-3
Multiplicative inverse
 7 22   161 506 
1  7 22 
  23
  

K  
17  21 9 
 21 9   483 207 
 5 12 

 
15 25 
1
Outline






Group, rings, and Fields
Modular arithmetic
Finite fields of the form GF(p)
Euclid’s algorithm (find GCD)
Polynomial arithmetic
Finite fields of the form GF(2n)
Motivation for GF(2n)

For a 8-bit block




Z256 ={0,1,…,255} is not a field => no division
The largest prime < 256 is 251
Z251 ={0,1,…,250} is a field => 251,…,255 are
wasted
Is that possible to find a field for Z256 ?

Yes. Define new arithmetic operations for Z256
Mapping from GF(2n) to
polynomials

Ex. 8-bit block
10010111
=>
1x  0 x  0 x  1x  0 x  1x  1x  1x
7
6
5
4
3
2
1
• To build the field for {0,1,2,…,2n-1}
=> Require modular polynomial arithmetic
0
Polynomial Arithmetic

Polynomials

3 polynomial arithmetic available:



ordinary polynomial arithmetic
Polynomial with coefficients in Zp; arithmetic on
the coefficients is performed modulo p
Polynomial with coefficients in Zp, and the
polynomials are defined modulo a polynomial
m(x); arithmetic on the coefficients is
performed modulo p
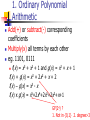
1. Ordinary Polynomial
Arithmetic



Add(+) or subtract(-) corresponding
coefficients
Multiply(x) all terms by each other
eg. 1101, 0111
f(x) = x3 + x2 + 1 and g(x) = x2 + x + 1
f(x) + g(x) = x3 + 2x2 + x + 2
f(x) – g(x) = x3 - x
f(x) x g(x) = x5+2x4+2x3+2x2+x+1

GF(24) ?
1. Not in {0,1} 2. degree>3
2. Polynomial Arithmetic with
Modulo Coefficients


Polynomial coefficients are in a field F={p,+,x}
We are most interested in coefficients in GF(2)
eg. 1101, 0111
3
2
2
 let f(x) = x + x + 1 and g(x) = x + x + 1
f(x) + g(x) = x3 + x
f(x) x g(x) = x5 + x + 1

GF(24) ?
degree > 3
3. Modular Polynomial Arithmetic
for GF(2n)

Polynomial coefficients are in a field
F={p,+,x}


Ex. coefficients are in GF(2)
If multiplication results in poly. of degree >
n-1
Reduce it by modulo some irreducible poly. m(x)
 f(x) = q(x) m(x) + r(x)
=> r(x) = f(x) mod m(x)


if m(x) has no divisors other than itself & 1
say it is irreducible (or prime) polynomial
GF(23)
=m(x)
Modular Polynomial Arithmetic

Computation in field GF(2n)




polynomials with coefficients modulo 2
whose degree is less than n
hence must reduce modulo an irreducible poly
of degree n (for multiplication only)
Can always find an inverse

Extended Euclid’s Inverse algorithm to find
Computational Considerations



since coefficients are 0 or 1, can represent
any such polynomial as a bit string
addition becomes XOR of these bit strings
multiplication is shift & XOR

modulo reduction done by repeatedly
substituting highest power with remainder of
irreducible poly (also shift & XOR) – see
textbook for details
Summary
Ciphertext: 2n
Plaintext: 2n
11010…0111
01100…0100
Mathematics
within GF(2n)