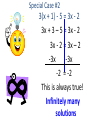Download Solving Equations With Variables on Both Sides of the = sign

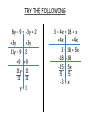
Solving Equations With Variables
on Both Sides of the equal sign
Introduction
• We’ve already worked on solving
– 1-step equations: x – 3 = 4
– 2-step equations: 2x + 8 = -10
– Multi-step equations: 5(a – 3) + a = 21
What happens if there is a variable on
both sides of the equal sign though?
3x + 2 = 4x - 1
Goal: Get the variable on one side of the equal (=) sign then
solve.
•To do this we have to move the smaller variable.
• How do we move a variable?
Apply the inverse operation to the whole term!
EXAMPLE
3x + 2 = 4x - 1
-3x
-3x
2=x-1
+1
3=x
+1
Important Notes
•Apply operations directly
below like terms!
•Bring equal sign straight
down
TRY THE FOLLOWING
8y – 9 = -3y + 2
+3y
+3y
11y – 9 = 2
+9
+9
11y = 11
11 11
y=1
3 – 4x = 18 + x
+4x
+4x
3 = 18 + 5x
-18 -18
-15 = 5x
5
5
-3 = x
Multi-Step Example
3(x + 4) = 2(x - 1)
3x + 12 = 2x - 2
-2x
-2x
x + 12 = - 2
-12 -12
x = - 14
• Distributive Property
• Then Solve!
Special Case #1
2x + 5 = 2x - 3
-2x
-2x
5 = -3
But is this possible?
NO!!!
So the answer is
NO SOLUTIONS
Special Case #2
3(x + 1) - 5 = 3x - 2
3x + 3 – 5 = 3x - 2
3x - 2 = 3x – 2
-3x
-3x
-2 = -2
This is always true!
Infinitely many
solutions
Your Favorite and Mine……
WORD PROBLEMS
Mr. Szabo needed to rent a moving van.
Company A charges a rate of $90 per hour
plus a $50 truck fee. Company B charges a
$70 per hour plus fee plus a $90 truck fee.
For what numbers of hours of rental is the
cost for the two companies the same?
Define our variables first!
• Let h = the number of hours of rental
Company A
$90 per hour plus $50
Company B
=
$70 per hour plus $90
90h + 50 = 70h + 90
-70h
-70h
20h + 50 = 90
-50 -50
20h = 40
20 20
h=2
Word Problem Answer
The rental cost for the two companies is the
same after 2 hours of rental.
Hours
Company A
Company B
h
90h + 50
70h + 90
0
$50
$90
1
$140
$160
2
$230
$230
3
$320
$300
LET’S PRACTICE