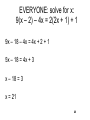Download Document

Welcome to MM150!
Unit 3 Seminar
To resize your pods:
Place your mouse here.
Left mouse click and hold.
Drag to the right to enlarge the pod.
To maximize chat,
minimize roster by
clicking here
MM150 Unit 3 Seminar Agenda
• Sections 3.1 -3.4
Examples
• Variables: x, y, z, a
• Algebraic Expression:
a+b
4x – 7
6y
x/4
They can be longer, like these:
3x2 – 7y3 + 12z – 2
a+b+c+d+e+f+g
Equations
• 2 + x = 11
• 3y - 9 = 36
• x/t = 64
• The solution to 2 + x = 11 is 9. We can
check the solution by substituting 9 for x.
• 2 + x = 11
• 2 + 9 = 11
4
• 11 = 11 This is a true statement.
Equations
• What happens if we end up with a false
statement?
• Is 10 a solution to 3y - 9 = 36? Check the
solution.
• 3y - 9 = 36
• 3(10) - 9 = 36
• 30 - 9 = 36
5
• 21 = 36 This statement is false.
Evaluating Expressions
• Exponents:
• x2
AND
34
AND
-7y3 AND 59
• 2*2*2*2*2*2*2, you can rewrite this as 27
x*x*x*x is x4
(2a)(2a)(2a) is (2a)3
(x + 6)(x + 6) is (x + 6)2
• x^2 is the same as x2
• 2^3 = 23 = 2*2*2 = 8
Be careful!
(-2)4 = (-2)(-2)(-2)(-2) = 16
-24 = -(2*2*2*2) = -16
6
•
Perimeter is the distance around a closed figure. The perimeter of a triangle can be
written as a + b + c, where a, b, and c are the side lengths of the triangle.
Example: The sides of a triangle have lengths of 3 meters, 7 meters, and x
meters. Determine the perimeter of the triangle if x is 10 meters .
Evaluate with x = 10
3 + 7 + 10 = 20 meters
•
The perimeter of the triangle is 20 meters.
Area is the measurement of surface measured in square units. The area of a
rectangle can be written as l * w, where l is the length and w is the width.
Example: Find the area of a rectangular yard enclosed by a fence 12 yards
long and 8 yards wide.
Evaluate with l = 12 and w = 8
12 * 8 = 96 square yards
Therefore, the area is 96 square yards.
EVERYONE:
•
Volume is space within a figure measured in cubed units. The volume of a cube can
be written as l * w * h, where l is the length, w is the width and h is the height.
Example: Find the volume of a cube with a length of 10 feet, a width of 4 feet and a
height of 3 feet.
Evaluate with l = 10, w = 4 and h = 3
8
EVERYONE: Answer
•
Volume is space within a figure measured in cubed units. The volume of a cube can
be written as l * w * h, where l is the length, w is the width and h is the height.
Example: Find the volume of a cube with a length of 10 feet, a width of 4 feet and a
height of 3 feet.
Evaluate with l = 10, w = 4 and h = 3
10 * 4 * 3 = 120 cubic feet
The volume is 120 cubic feet.
9
Terms
• Examples of terms:
Constants: 3, -5, 0, 1/7, Pi
Variables: a, b, c, x, y, z
Products: 3x, ab2, -99ay5
Expressions can be one term (monomial): x, 5t,
-10y
Expressions can have two terms (binomial): y + 9, -6s - 11
Expressions can have three terms (trinomial): x2 + 7x - 10
Expressions can have four terms or more (polynomial):
x2y + xy - 11y + 23
NOTE: Decreasing power of the variable.
10
Like and Unlike Terms
• 5x and 3x are like terms
6ab and -9ab are like terms
16x2 and x2 are like terms
-0.35ac5 and -400ac5 are like terms
You can simplify like terms! For example,
12a + 4a = 16a
57x – 33x = 24x
9x2 + 3x2 + x2 = 13x2
-ab + (-4ab) = -5ab
You cannot simplify unlike terms!!
2x + 2y + 3x = 5x + 2y
11
11
Addition Property of Equality
For real numbers a, b, and c,
if a = b, then a + c = b + c.
Example:
If x = 4,
then x + 2 = 4 + 2
Non example:
If y = 9, then y + 7 = 9
Here we only added 7 to one side
Here we added 2 to both sides
12
Solving Equations
• x - 7 = 18
• x - 7 + 7 = 18 + 7
• x = 25
• 12 = -4 + x
• 12 + 4 = -4 + x + 4
• 16 = x
• EVERYONE: 6 = x - 22. What is x?
13
Example: 5 + 6 + x = 11 – 2
11 + x = 9
11 + x – 11 = 9 – 11
x = -2
14
EVERYONE: solve for x:
2–8=x–5–1
-6 = x – 6
0=x
15
Multiplication Property of
Equality
For real numbers a, b, and c, where c is not
0, if a = b, then a * c = b * c.
Example:
If x = 4,
then x * 2 = 4 * 2
Non example:
If y = 9, then y * 7 = 9
Here we only multiplied 7 to one side
Here we multiplied by 2 to both sides
16
Solving Equations
• Example: (2/3)x = 4/5
(3/2)(2/3)x = (3/2)(4/5)
x = 12/10
x = 6/5
Example: x/6 = -1/2
6(x/6) = 6(-1/2)
x = -6/2
x = -3
17
Division Property of Equality
For real numbers a, b, and c, where c is not
0, if a = b, then a/c = b/c.
Example:
If x = 4,
then x/2 = 4/2
Non example:
If y = 9, then y/7 = 9
Here we only divided one side
Here we divided both sides by 2
18
Solving Equations
• Example: -3x = 18
-3x/(-3) = 18/(-3)
x = -6
Example: 9x = -8
9x/9 = -8/9
x = -8/9
Example: -x = -3
-1(-x) = -1(-3)
x=3
-x/(-1) = -3/(-1)
19
Example: 3 – 12x = 3x + 20
3 = 15x + 20
-17 = 15x
-17/15 = x
20
EVERYONE: solve for x:
22 + 3 – 6x = 2x + x + 11
25 – 6x = 3x + 11
25 = 9x + 11
14 = 9x
14/9 = x
21
Example:
3(2x – 5) – 7 = x(x + 4) – x2
6x – 15 – 7 = x2 + 4x – x2
-22 = -2x
11 = x
22
EVERYONE: solve for x:
9(x – 2) – 4x = 2(2x + 1) + 1
9x – 18 – 4x = 4x + 2 + 1
5x – 18 = 4x + 3
x – 18 = 3
x = 21
23
Example: (1/2)x + 5/4 = 7/4
4[(1/2)x + (5/4)] = 4[7/4]
4[(1/2)x] + 4[5/4] = 4[7/4]
2x + 5 = 7
2x = 2
x=1
24
Example: 0.3x + 1.4 = 2.25x – 9.02
100[0.3x] + 100[1.4] = 100[2.25x] – 100[9.02]
30x + 140 = 225x – 902
140 = 195x – 902
1042 = 195x
1042/195 = x
25
Special Cases
• Example: 2x + 3 = 3 + 2x
2x + 3 – 2x = 3 + 2x – 2x
3=3
Example: x + 3 = x – 5
x+3–x=x–5–x
3 = -5
26
Solving for a Variable
• Example: solve a + b = c for a
a+b–b=c–b
a=c–b
Example: solve A = (1/2)bh for h
2*A = 2*(1/2)bh
2A = bh
2A/b = bh/b
2A/b = h
27
Translating to Math
•
Ex. three plus a number
3+x
Ex. ten more than a number
N + 10
Ex. 9 minus a number
9–x
Ex. 20 decreased by an unknown number
***Ex. 4 less than a number
Ex. 4 times a number
20 – n
x–4
4 * x OR 4x
Ex. a number times a different number
Ex. 7 divided by a number
7/x
Ex. A number divided by 2
n/2
x * y OR
xy.
28
Ex. A number squared increased by six
x2 + 6
Page 139 #34
• PetSmart has a sale offering 10% off of all
pet supplies. If Amanda spent $15.72 on
pet supplies before tax, what was the
price of the pet supplies before the
discount?
•
•
•
•
•
Name the price before discount x.
x - x * 0.10 = 15.72
x - 0.10x = 15.72
0.9x = 15.72
x is about $17.47
29
Page 140 #46
•
A bookcase with three shelves is built by a student. If the height of the
bookcase is to be 2 ft longer than the length of a shelf and the total amount
of wood to be used is 32 ft, find the dimensions of the bookcase.
•
Let x = width (length of shelf) and let x + 2 = height
•
From picture in book, there are 4 pieces of wood for width and 2 pieces of
wood for the height.
•
4x + 2(x + 2) = 32
•
4x + 2x + 4 = 32
•
6x + 4 = 32
•
6x = 28
•
x = 28/6
•
x = 14/3 = 4 2/3
•
So, width of bookcase is 4 2/3 ft and height is 6 2/3 ft.
30