Download Unit 1: Functions

Unit 1: Functions
Lesson 1: Relations and Functions
Learning Goals:
 I can determine if a relation is a function
Unit 1: Functions
Lesson 1: Relations and Functions
So far, we have seen mathematical relationships written
like this:
These examples are relations: They
are rules describing the
• y = 3x + 1 relationship between the dependent
• y = 2x2 -2 and independent variables.
A relation is a connection (or
2
• y = x
relationship) between two sets of
numbers, such as height vs. time or
• y = 5x
cost vs. weight
• Etc, etc.
The Dependent Variable is:
The Independent Variable is:
Unit 1: Functions
Lesson 1: Relations and Functions
Example: The height, h, of an object thrown up in
the air is dependent on the time, t. “h” is
dependent on “t”, therefore h is the dependent
variable and t is the independent variable.
Unit 1: Functions
Lesson 1: Relations and Functions
These examples
represent function
notation and are read as,
“ f of x”, or “f at x”.
Unit 1: Functions
Lesson 1: Relations and Functions
Function notation represents a relation
where there is only one unique value of
the function (f) for any value of x.
In other words, each x-value
(independent variable) has only one yvalue (dependent variable)
Unit 1: Functions
Lesson 1: Relations and Functions
How do you know whether something is
a function?
• If you put in a value for “x” and
there is only one value for “y” it is a
function.
• If you put in a value for “x” and get
more than one value for “y”, it is not
a function.
Unit 1: Functions
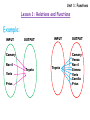
Lesson 1: Relations and Functions
Example:
INPUT
OUTPUT
INPUT
Camary
Rav 4
Yaris
Prius
Toyota
Toyota
OUTPUT
Camary
Venza
Rav 4
Sienna
Yaris
Corolla
Prius
Unit 1: Functions
Lesson 1: Relations and Functions
A function can be represented by:
1) A Table of Values
2) A Set of Ordered Pairs
3) A Mapping Diagram
4) A Graph
5) An Equation
Unit 1: Functions
Lesson 1: Relations and Functions
Table of Values: It is a function if each x-value only
corresponds to
one y-value
x
-2
-1
0
-1
y
3
2
1
0
x
1
3
7
2
y
5
6
8
8
Unit 1: Functions
Lesson 1: Relations and Functions
Ordered Pairs: It is a function if for each xvalue there is only
one y-value
f = {(1,-4), (2, 5), (8, 9), (0, 6)}
g = {(1, -3), (2, -3), (3, 0), (2, 0)}
Unit 1: Functions
Lesson 1: Relations and Functions
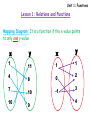
Mapping Diagram: It is a function if the x-value points
to only one y-value
x
1
4
7
10
y
x
11
1
8
0
10
-1
9
y
1
2
3
4
Unit 1: Functions
Lesson 1: Relations and Functions
Graph: It is a function if it passes the vertical
line test.
Vertical Line Test: Draw a vertical line through
the graph. If the line crosses the graph more
than once it is not a function.
Unit 1: Functions
Lesson 1: Relations and Functions
Equation: Anything in the form
y = mx + b is a function.
Anything in the form
y = ax2+ bx + c is a function. To
check anything else, graph it!
Unit 1: Functions
Lesson 1: Relations and Functions
Determine whether the following relations are
functions or not
a) y = 2x + 1
b) y = 2x2 - 3
c) x2 + y2 = 4
Unit 1: Functions
Lesson 1: Relations and Functions
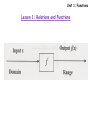
Domain: The set of all the input values that are
defined for a function. (Formerly referred to as
the x-values or the independent variable.) Written
from smallest to largest number.
Range: The set of all the output values for the
function. Can be determined by subbing in the
values from the domain. (Formerly referred to as
the y-values or the dependent variable.) Also
written from smallest to largest number.
Unit 1: Functions
Lesson 1: Relations and Functions
Unit 1: Functions
Lesson 1: Relations and Functions
Example: Write the domain and range for this
function using set notation.
x
1
3
7
2
y
5
6
8
8
Unit 1: Functions
Lesson 1: Relations and Functions
Example: Write the domain and range for this
function using set notation.
f = {(1,-4), (2,5), (8, 9), (0, 6)}
Unit 1: Functions
Lesson 1: Relations and Functions
Example: Write the domain and range for this
function using set notation.
x
1
4
7
10
y
11
8
10
9
Unit 1: Functions
Lesson 1: Relations and Functions
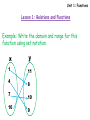
Example: Write the domain and range for this
function using set notation.
Unit 1: Functions
Lesson 1: Relations and Functions
Practice
Level 4: pg. 10-12 # 1 – 12, 14
Level 3: pg. 10-12 # 1 – 10, 14
Level 2: Pg. 10-12 #1-7, 14
Level 1: Pg. 10-12 #1 -3, 14