Download Slide 1

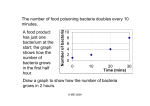
Chapter 2 – Linear and Exponential Functions
2.1 – Introducing Linear Models
2.2 – Introducing Exponential Models
2.3 – Linear Model Upgrades
2.1
A linear function models any process that has a constant rate of
change.
m = change in y-value
change in x-value
The graph of a linear function is a straight line.
A linear function has the form:
y = f(x) = b + mx
where
f is the name of the function.
b is the starting value or y intercept (f(0)).
m is the constant rate of change or slope.
slope intercept form
2.1
In summer of 2001, the exchange rate for the Mexican peso was 9.2.
x
(dollar)
0
1
2
3
10
y
(peso)
0
9.2
18.4
27.6
92
x
0 to 1
1 to 2
0 to 3
1 to 10
change in x
1
1
3
9
y
0 to 9.2
9.2 to
18.4
0 to 27.6
9.2 to 92
change in y
9.2
9.2
27.6
82.8
m
9.2/1
9.2
9.2/1
9.2
27.6/3
9.2
82.8/9
9.2
CONSTANT RATE OF CHANGE
Mexican peso conversion is a linear function with respect to US dollar.
2.1
In summer of 2001, the exchange rate for the Mexican peso was 9.2.
pesos
dollars
straight line graph
Mexican peso conversion is a linear function with respect to US dollar.
2.1
In summer of 2001, the exchange rate for the Mexican peso was 9.2.
p(d) = 9.2*d
linear formula: f(x) = b + mx
starting value/y-intercept (b) is 0.
rate of change/slope (m) is 9.2.
Mexican peso conversion is a linear function with respect to US dollar.
2.1
Jason decides to purchase a $3000 DJ system that has a life expectancy of
10 years. He assumes the value of the equipment will depreciate linearly by
the same amount ($300) each year .
x
(age)
0
1
2
3
4
5
6
7
8
9
10
y
(value)
3000
2700
2400
2100
1800
1500
1200
900
600
300
0
x
0 to 1
1 to 2
0 to 5
3 to 10
change in x
1
1
5
7
y
3000 to
2700
2700 to
2400
3000 to
1500
2100 to 0
change in y
-300
-300
-1500
-2100
m
-300/1
-300
-300/1
-300
-1500/5
-300
-2100/7
-300
CONSTANT RATE OF CHANGE
Value of DJ system is a linear function with respect to age.
2.1
Jason decides to purchase a $3000 DJ system that has a life expectancy of
10 years. He assumes the value of the equipment will depreciate linearly by
the same amount ($300) each year .
value
(dollars)
age (years)
straight line graph
Value of DJ system is a linear function with respect to age.
2.1
Jason decides to purchase a $3000 DJ system that has a life expectancy of
10 years. He assumes the value of the equipment will depreciate linearly by
the same amount ($300) each year .
v(t) = 3000 - 300*t
linear formula: f(x) = b + mx
starting value/y-intercept (b) is 3000 [$].
rate of change/slope (m) is -300 [$ per year].
Value of DJ system is a linear function with respect to age.
2.1
Under America Online’s Unlimited Usage plan, a member is charged $21.95
per month regardless of the number of hours spent online. Express the
monthly bill as a function of the number of hours used in one month.
t
(hours)
0
1
2
10
20
100
bill
(dollars)
21.95
21.95
21.95
21.95
21.95
21.95
x
0 to 1
1 to 2
2 to 10
1 to 20
change in x
1
1
8
19
y
21.95 to
21.95
21.95 to
21.95
21.95 to
21.95
21.95 to
21.95
change in y
0
0
0
0
m
0/1
0
0/1
0
0/8
0
0/19
0
CONSTANT RATE OF CHANGE
Monthly bill is a linear function with respect to number of hours used.
2.1
Under America Online’s Unlimited Usage plan, a member is charged $21.95
per month regardless of the number of hours spent online. Express the
monthly bill as a function of the number of hours used in one month.
bill (dollars)
time (hours)
STRAIGHT LINE GRAPH
Monthly bill is a linear function with respect to number of hours used.
2.1
Under America Online’s Unlimited Usage plan, a member is charged $21.95
per month regardless of the number of hours spent online. Express the
monthly bill as a function of the number of hours used in one month.
U(t) = 21.95
linear formula: f(x) = b + mx
starting value/y-intercept (b) is 21.95 [$].
rate of change/slope (m) is 0 [$ per hour].
Monthly bill is a linear function of number of hours spent online.
2.1
Not all straight line graphs are linear functions.
Consider the equation x = 3.
x
3
3
3
3
3
y
-4
-1
0
3
5
x
3 to 3
3 to 3
3 to 3
3 to 3
change in x
0
0
0
0
y
-4 to
1
-4 to 0
-1 to 0
0 to 5
change in y
5
4
1
5
m
5/0
u
4/0
u
1/0
u
5/0
u
linear formula: f(x) = b + mx
7/81
7
10/81
21
An exponential function models any process in which function
values change by a fixed ratio or percentage.
The graph of an exponential function is curvy.
An exponential function has the form:
y = f(x) = c * ax
where
f is the name of the function.
c is the starting value or y intercept (f(0)).
a is the growth factor.
2.2
Harmful kitchen bacteria can double their numbers every 20 minutes. A
single bacterium on a wet countertop might in just eight hours, reproduce to
nearly 17 million.
t
(20 minute intervals)
0
1
2
3
4
5
P
(number of bacteria)
1
2
4
8
16
32
t
0 to 1
1 to 2
change in t
1
1
P
1 to 2
2 to 4
change in P
1
2
m
1/1
1
2/1
2
NO CONSTANT RATE OF CHANGE [increasing].
2.2
Harmful kitchen bacteria can double their numbers every 20 minutes. A
single bacterium on a wet countertop might in just eight hours, reproduce to
nearly 17 million.
t
(20 minute intervals)
0
1
2
3
4
5
P
(number of bacteria)
1
2
4
8
16
32
ratio of consecutive output values
t
P(t+1)/P(t)
0
P(1)/P(0) = 2 / 1 = 2
1
P(2)/P(1) = 4 / 2 = 2
2
P(3)/P(2) = 8 / 4 = 2
Growth factor is 2 [doubling].
Harmful kitchen bacteria can double their numbers every 20 minutes. A
single bacterium on a wet countertop might in just eight hours, reproduce to
nearly 17 million.
bacteria
population
time (20-minute intervals)
GRAPH IS CONCAVE UP [increasing rate of change].
Harmful kitchen bacteria can double their numbers every 20 minutes. A
single bacterium on a wet countertop might in just eight hours, reproduce to
nearly 17 million.
P(t) = 2t
exponential formula: f(x) = c*ax
starting value/y-intercept (c) is 1 [bacteria].
growth factor (a) is 2.
Bacteria population is an exponential function of time.
After 8 hours (24 20-minute time intervals):
P(24) = 224 = 16,777,216 bacteria
During the late twentieth century, WHO adopted as one of its goals the
elimination of polio throughout the world. From 1988 to 1996, cases of polio
decreased by roughly 25% annually.
t
(years since 1988)
0
1
2
3
P
(polio cases)
38,000
38000-.25*38000
= 28500
28500-.25*28500
= 21375
21375-.25*21375
= 16031
t
0 to 1
1 to 2
change in t
1
1
P
38000
to
28500
28500
to
21375
change in P
-9500
-7125
m
-9500
-7125
NO CONSTANT RATE OF CHANGE [increasing].
During the late twentieth century, WHO adopted as one of its goals the
elimination of polio throughout the world. From 1988 to 1996, cases of polio
decreased by roughly 25% annually.
t
(years since
1988)
0
1
2
3
P
(polio cases)
38,000
38000-.25*38000
= 28500
28500-.25*28500
= 21375
21375-.25*21375
= 16031
ratio of consecutive output values
t
P(t+1)/P(t)
0
P(1)/P(0) = 28500 / 38000 = .75
1
P(2)/P(1) = 21375 / 28500 = .75
2
P(3)/P(2) = 16031 / 21375 = .7499
“growth” factor is 0.75 [decreasing by 25% means 75% remains]
During the late twentieth century, WHO adopted as one of its goals the
elimination of polio throughout the world. From 1988 to 1996, cases of polio
decreased by roughly 25% annually.
number of polio
cases
years since 1988
GRAPH IS CONCAVE UP [increasing rate of change].
During the late twentieth century, WHO adopted as one of its goals the
elimination of polio throughout the world. From 1988 to 1996, cases of polio
decreased by roughly 25% annually.
P(t) = 38000*(.75)t
exponential formula: f(x) = c*ax
starting value/y-intercept (c) is 38000 [polio cases].
growth factor (a) is 0.75.
Number of polio cases is an exponential function of time.
Chapter 2 – Linear and Exponential Functions
HWp81: #1-23
TURN IN: #5, #9, #20 (reference #19), #22,