Download EE121Lec13

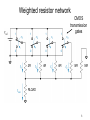
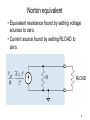
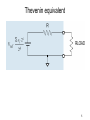
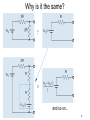
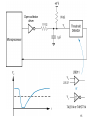
EE121
John Wakerly
Lecture #13
Digital-to-analog conversion
Analog-to-digital conversion
1
Digital-to-analog conversion
Vout = k (x020 + x020 + x020 + … + xn-12n-1) / 2n
reference voltage in “multiplying” DAC
k / 2n = “step size”
2
Weighted resistor network
CMOS
transmission
gates
3
Norton equivalent
• Equivalent resistance found by setting voltage
sources to zero.
• Current source found by setting RLOAD to
zero.
4
Thevenin equivalent
5
Weighted-resistor network problems
• Resistor values span a wide range
– n-bit DAC ==> resistors from 2R to 2nR
– 8-bit DAC ==> 2R to 512R, e.g., 2K to 512K
– Difficult to fabricate wide ranges of resistance in
semiconductor processes.
• Different resistors in the network have different
accuracy requirements.
– 5% resistance change at MSB has 2.5% effect
– 5% resistance change at LSB (8-bit) has .02% effect
– MSB of 16-bit DAC (as in CD player) would require
accuracy of one part in 215 (.003%) to have less than
one step-size error.
6
Solution: Ladder Network
• Same Norton and Thevenin equivalents
• Uses only two resistor values, R and 2R
– Easy to control resistance ratios on-chip
7
Why is it the same?
and so on...
8
Analog-to-digital conversion
• Analog comparator = 1-bit A-to-D
9
Combinational A-to-D
• Fastest conversion time
– used in digital scopes, video sampling, etc.
• Good for only a few bits of resolution
10
Sequential A-to-D
• Idea: Use one comparator, repetitively, and a
DAC to try different digital values until correct
result is found.
“COMP”
(logic signal)
RESULT
11
Counter-ramp A-to-D
• Initialize result register to 0
• Keep incrementing result register until the
DAC produces a votage greater than Vin.
• Maximum of 2n steps for n-bit conversion.
• ABEL code:
state IDLE: if START then LOOK with result := 0;
else IDLE with result := result;
state LOOK:
if (COMP == 1) then DONE with result := result;
else if (result == MAX) then DONE with result := result;
else LOOK with result := result + 1;
state DONE: if START then DONE with result := result;
else IDLE with result := result;
12
Successive-approximation A-to-D
• Like a binary search in software -- n steps to
search 2n possible results (n-bit result).
• First step -- determine MSB of result:
– Set result to 100…00. Is COMP 1 or 0?
– COMP=1 ==> MSB = 1; else MSB = 0.
• Second step -- determine next lower bit:
– Set result to x10…00. Is COMP 1 or 0? (x = bit
found at previous step).
– COMP=1 ==> next lower bit =1; else 0.
• And so on, for n steps through the LSB
• Lab assignment -- create state machine and
result register for this algorithm in ABEL.
13
Apple ][ A-to-D converter
• Converts analog position into numeric value.
• Idea:
– Use a potentiometer whose resistance is a function
of position (e.g., on a joystick).
– Combine the resistance with a capacitance and
measure the RC time constant use a program loop.
14
15
Next Time
• Read-only memories (review)
• Read-write memories
• SRAMs
• DRAMs
16