Download this slide show on Kirchhoff

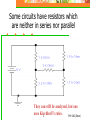
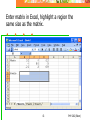
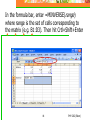
Kirchhoff’s Rules
When series and parallel
combinations aren’t enough
PHY 202 (Blum)
1
Some circuits have resistors which
are neither in series nor parallel
They can still be analyzed, but one
uses Kirchhoff’s
rules.
2
PHY 202 (Blum)
Not in series
The 1-k resistor is not in series with the 2.2-k since the
some of the current that went through the 1-k might go
through the 3-k instead of the 2.2-k resistor.
3
PHY 202 (Blum)
Not in parallel
The 1-k resistor is not in parallel with the 1.5-k since their
bottoms are not connected simply by wire, instead that 3-k
lies in between.
4
PHY 202 (Blum)
Kirchhoff’s Node Rule





A node is a point at which wires meet.
“What goes in, must come out.”
Recall currents have directions, some currents will
point into the node, some away from it.
The sum of the current(s) coming into a node must
equal the sum of the current(s) leaving that node.
 I2
I1 
I 1 + I 2 = I3
The node rule is about currents!
5
 I3
PHY 202 (Blum)
Kirchhoff’s Loop Rule 1
“If you go around in a circle, you get
back to where you started.”
 If you trace through a circuit keeping
track of the voltage level, it must return
to its original value when you complete
the circuit


Sum of voltage gains = Sum of voltage losses
6
PHY 202 (Blum)
Batteries (Gain or Loss)
Loop direction
Whether a battery is a gain or a loss
depends on the direction in which you
are tracing through the circuit
Loop direction

Loss
Gain
7
PHY 202 (Blum)
Resistors (Gain or Loss)
Loop direction
Current direction
Loss
I
Gain
8
I
Current direction
Whether a resistor is a gain or a loss
depends on whether the trace direction
and the current direction coincide or not.
Loop direction

PHY 202 (Blum)
Neither Series Nor Parallel
JB
JA
JC
Draw loops such that each current element is included
in at least one loop. Assign current variables to each
loop. Current direction and lop direction are the same.
9
PHY 202 (Blum)
Currents in Resistors



Note that there are two currents associated with the
2.2-kΩ resistor. Both JA and JC go through it.
Moreover, they go through it in opposite directions.
When in Loop A, the voltage drop across the 2.2-kΩ
resistor is 2.2(JA-JC)
On the other hand, when in Loop C, the voltage drop
across the 2.2-kΩ resistor is 2.2(JC-JA) the opposite
sign because we are going through the resistor in the
opposite direction.
PHY 202 (Blum)
10
Loop equations
5 = 1  (JA - JB) + 2.2  (JA - JC)
 0 = 1 (JB - JA) + 1.5  JB + 3 (JB JC)
 0 = 2.2 (JC - JA) + 3 (JC - JB) + 1.7 JC

 “Distribute” the parentheses
5 = 3.2
JA – 1 JB - 2.2 JC
 0 = -1 JA + 5.5
JB – 3 JC
 0 = -2.2JA – 3 JB + 6.9 JC

11
PHY 202 (Blum)
Loop equations as matrix equation
5 = 3.2
JA – 1 JB - 2.2 JC
 0 = -1 JA + 5.5
JB – 3 JC
 0 = -2.2JA – 3 JB + 6.9 JC

 3.2  1  2.2  J A  5
  1 5.5  3   J   0

 B   
 2.2  3 6.9   J C  0
12
PHY 202 (Blum)
Enter matrix in Excel, highlight a region the
same size as the matrix.
13
PHY 202 (Blum)
In the formula bar, enter =MINVERSE(range)
where range is the set of cells corresponding to
the matrix (e.g. B1:D3). Then hit Crtl+Shift+Enter
14
PHY 202 (Blum)
Result of matrix inversion
15
PHY 202 (Blum)
Prepare the “voltage vector”, then highlight a range the same size as the
vector and enter =MMULT(range1,range2) where range1 is the inverse
matrix and range2 is the voltage vector. Then Ctrl-Shift-Enter.
Voltage vector
16
PHY 202 (Blum)
Results of Matrix Multiplication
17
PHY 202 (Blum)