Download PPT

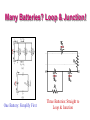
Physics 2113
Jonathan Dowling
Lecture 21: MON 12 OCT
Circuits III
RC Circuits: Charging a Capacitor
In these circuits, current will change for a while, and then stay constant.
We want to solve for current as a function of time i(t)=dq/dt.
The charge on the capacitor will also be a function of time: q(t).
The voltage across the resistor and the capacitor also change with time.
To charge the capacitor, close the switch on a.
E + VR (t) + VC (t) = 0
VC=Q/C
VR=iR
E - i(t)R - q(t) /C = 0
E - ( dq /dt ) R - q(t) /C = 0
A differential equation for q(t)! The solution is:
Time constant:  = RC
q(t) = CE (1- e-t / RC )
Time i drops to 1/e.
-t / RC
® i(t) º dq /dt = (E /R)e
i(t)
E/R
CE
t
t
RC Circuits: Discharging a Capacitor
Assume the switch has been closed
on a for a long time: the capacitor will
be charged with Q=CE.
+++
---
Then, close the switch on b: charges find their way across the circuit,
establishing a current.
V +V = 0
R
C
-i(t)R + q(t) /C = 0 ® ( dq /dt ) R + q(t) /C = 0
+
-C
-t / RC
-t / RC
q(t)
=
q(0)e
=
CEe
Solution:
i(t) = dq /dt = (q(0) /RC)e-t / RC = (E /R)e-t / RC
i(t)
E/R
t
t
(a) Compare i(0) = E / R
i1 = 6, i2 = 4, i3 = 1, i4 = 2
i1 > i2 > i4 > i3
(b) Compare t = RC
t 1 = 6, t 2 = 6, t 3 = 5, t 4 = 10
t 4 > t1 = t 2 > t 3
Time constant:  = RC
Time i drops to 1/e≅1/2.
i(t)
E/R
t
Example
The three circuits below are connected to the same ideal
battery with emf E. All resistors have resistance R, and all
capacitors have capacitance C.
•Which capacitor takes the longest in getting charged?
•Which capacitor ends up with the largest charge?
• What’s the final current delivered by each battery?
•What happens when we disconnect the battery?
Simplify R’s into
into Req. Then apply charging
formula with ReqC = 
Ifcapacitorsbetween
resistorsinparallel
uselooprule.
Example
In the figure, E = 1 kV, C = 10 µF, R1 = R2 = R3 = 1
M. With C completely uncharged, switch S is suddenly
closed (at t = 0).
• What’s the current through each resistor at t=0?
• What’s the current through each resistor after a long
time?
• How long is a long time?
At t=0 replace capacitor with
solid wire (open circuit) then use
loop rule or Req series/parallel.
Att>>0replacecapacitor
withbreakinwire,i3=0,and
useloopruleonR1 andR2
branchonly.Alongtimeis
t>>𝜏.
RC Circuits: Charging a Capacitor
In these circuits, current will change for a while, and then stay constant.
We want to solve for current as a function of time i(t)=dq/dt.
The charge on the capacitor will also be a function of time: q(t).
The voltage across the resistor and the capacitor also change with time.
To charge the capacitor, close the switch on a.
E + VR (t) + VC (t) = 0
VC=Q/C
VR=iR
E - i(t)R - q(t) /C = 0
E - ( dq /dt ) R - q(t) /C = 0
A differential equation for q(t)! The solution is:
Time constant:  = RC
q(t) = CE (1- e-t / RC )
Time i drops to 1/e.
-t / RC
® i(t) º dq /dt = (E /R)e
i(t)
E/R
CE
t
t
RC Circuits: Discharging a Capacitor
Assume the switch has been closed
on a for a long time: the capacitor will
be charged with Q=CE.
+++
---
Then, close the switch on b: charges find their way across the circuit,
establishing a current.
V +V = 0
R
C
-i(t)R + q(t) /C = 0 ® ( dq /dt ) R + q(t) /C = 0
+
-C
-t / RC
-t / RC
q(t)
=
q(0)e
=
CEe
Solution:
i(t) = dq /dt = (q(0) /RC)e-t / RC = (E /R)e-t / RC
i(t)
E/R
t
t
• Fire Hazard: Filling gas can in pickup truck with plastic bed liner.
• Safe Practice: Always place gas can on ground before refueling.
• Touch can with gas dispenser nozzle before removing can lid.
• Keep gas dispenser nozzle in contact with can inlet when filling.
One Battery? Simplify!
Resistors
Key formula: V=iR
In series: same current dQ/dt
Req=∑Rj
In parallel: same voltage
1/Req= ∑1/Rj
P = iV = i2R = V2/R
Capacitors
Q=CV
same charge Q
1/Ceq= ∑1/Cj
same voltage
Ceq=∑Cj
U = QV/2 = Q2/2C = CV2
Many Batteries? Loop & Junction!
One Battery: Simplify First
Three Batteries: Straight to
Loop & Junction
1
1
1
=
+ ® R23par = 12W
par
R23
R2 R3
Too Many Batteries!