Download IB Physics

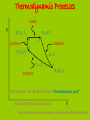
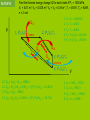
IB Physics
Topic 10 – Thermodynamic Processes
Mr. Jean
The plan:
• Video clip of the day
– https://www.youtube.com/watch?v=nBVL3lp9f
Go
– https://www.youtube.com/watch?v=s3tjOEtoAr
g
• Returning Exams
• Thermodynamic processes
Returning Exams:
• Review your exams
• If you have any questions we can go over
some of the solutions briefly.
Gravitational Waves:
• https://www.youtube.com/watch?v=gwi_VKd6Wo
Combining the gas laws gives
PV = (a constant)×T
Therefore, for n moles of an ideal gas;
P = Pressure
PV = nRT
V = Volume
n = number of moles
R = Universal gas constant
T = Temperature (KELVIN)
Deduce an expression
for the work involved in a
volume change of a gas
at constant pressure.
The work done by this force is w = Fs = PAs,
since F=PA
but As is the change in the volume occupied by the gas, ΔV.
therefore;
W = PDV
State the first law of thermodynamics.
We can add energy to a gas by heating Q
(temperature gradient)
Or by working (mechanical energy) = W
Q = ΔU + W
Q = Heat energy added to the
ΔU = Internal energy
increase of the gas
W = Work done by the gas.
Students should be familiar with
the terms system and
surroundings. They should also
gas appreciate that if a system and
its surroundings are at different
temperatures and the system
undergoes a process, the
energy transferred by nonmechanical means to or from
the system is referred to as
thermal energy (heat).
1. Change of p (and T) at
constant volume; an
isovolumetric change.
2. Change of V (and T) at
constant pressure; an
isobaric change.
3. Change in p and V at
constant temperature;
an isothermal change.
4. Change in p and V in an
insulated container (no
heating of the gas); an
adiabatic change.
The product of pressure and volume represents a quantity of
work. This is represented by the area below a p-V curve.
Therefore, the area enclosed by the four curves represents the
net work done by the engine during one cycle.
Second Law of Thermodynamics: It is impossible to
extract an amount of heat QH from a hot reservoir
and use it all to do work W . Some amount of heat QC
must be exhausted to a cold reservoir.
Entropy is a measure of the disorder (of the
energy) of a system
Every time we change energy from one form to
another, we increase the entropy of the
Universe even though local entropy may
decrease.
Thermodynamic Processes
A system can change its state
A state is a unique set of values for P, V, n, & T
(so PV = nRT is also called a “State Equation”)
When you know the state of a system you know U since
U =  NkT =  nRT =  PV, for a monatomic gas
A “process” is a means of going from 1 state to another
There are 4 basic processes with n constant
“iso” means “same”
Isobaric, a change at constant pressure
Isochoric or isovolumetric, a change at constant volume, W = 0
Isothermal, a change at constant temperature (DU = 0, Q = W)
Adiabatic, a process is one in which no heat is gained or
lost by the system.
Thermodynamic Processes
Isobar
P
(P1,V1) T1
(P2,V2) T2
1
Isochore
(P4,V4) T4
2
Adiabat
4
Q=0
T3 = T4
Isotherm
3
(P3,V3) T3
The trip from 12341 is call a “thermodynamic cycle”
Each part of the cycle is a process
V
All state changes can be broken down into the 4 basic processes
Thermodynamic Processes
Isobar, expansion at constant pressure, work is done
P
1
Isochoric
4
pressure
change, W = 0
2
Adiabatic expansion;
no heat, Q = 0
3
Isothermal
compression
W = Q, U is
constant
The area enclosed by the cycle
is the total work done, W
The work done, W, in a cycle is
+ if you travel clockwise
V
Heat Engines and Refrigerators
Engines use a working fluid, often a gas, to create
motion and drive equipment; the gas moves from 1
state (P, V, n, & T define a state) to another in a cycle
The Stirling Cycle:
2 isotherms
2 isochores
Stirling designed this engine in the early
18th century – simple and effective
The Stirling Engine
Isobaric expansion of a piston
in a cylinder
The work done W = Fd = PAd = PDV
The work done is the area under the process W = PDV
4 stroke engine
Isochoric expansion of a
piston in a cylinder
The work done W = 0 since there is no change in volume
Thus DU = Q – W = Q
Adiabatic expansion of
an ideal gas
The work done W = 0 here because chamber B is empty and P = 0
Thus DU = Q – W = 0, that is adiabatic expansion
against no resistance does not change the internal
energy of a system
EXAMPLE
How much work is done by the system when the system is taken from:
(a) A to B (900 J)
(b) B to C (0 J)
(c) C to A (-1500 J)
Each rectangle on the graph
represents 100 Pa-m³ = 100 J
(a) From A B the area is 900 J,
isobaric expansion
(b) From B  C, 0, isovolumetric change of pressure
(c) From C A the area is -1500 J
EXAMPLE
10 grams of steam at 100 C at constant pressure rises to 110 C:
P = 4 x 105 Pa
DT = 10 C
DV = 30.0 x 10-6 m3
c = 2.01 J/g
What is the change in internal energy?
DU = Q – W
DU = mcDT – PDV
DU = 189 J
So heating the steam produces a
higher internal energy and expansion
EXAMPLE
Aluminum cube of side L is heated in a chamber at atmospheric pressure.
What is the change in the cube's internal energy if L = 10 cm and DT = 5 °C?
DU = Q – W
Q = mcDT
m = V0
V0 = L3
W = PDV
DV = V0DT
DU = mcDT – PDV
cAl = 0.90 J/g°C
DU = V0cDT – PV0DT
Al = 72(10-6) °C-1
DU = V0DT (c – P)
Patm = 101.5 kPa
Al = 2.7 g/cm³
DU = L³DT (c – P)
DU = 0.10³(5)((2700)(900) – 101.5(10³)(72(10-6))
DU = 12,150 J
NB: P is neglible
EXAMPLE
Find the work done for a cycle if P1 = 1000 kPa, V1 = 0.01 m³,
V2 = 0.025 m³, V3 = V4 = 0.04 m³, T1 = 400 K, T2 = 600K, n = 2 mol
W = Area enclosed
= P1DV12 +  (P2+P3)DV23 –  (P1+P4)DV41
P
1, (P1,V1) T1 Isobar
2, (P2,V2) T2
3, (P3,V3) T3
Isochore
4, (P4,V4) T4
1. P2 = P1 = 1000 kPa
2. T4 = T1 = 400 K
3. T3 = T2 = 600 K
4. P3 = P2V2/V3 = 625 kPa
5. P4 = P1V1/V4 = 250 kPa
V
W = Area enclosed
= P1DV12 +  (P2+P3)DV23 +  (P1+P4)DV41
= (15 + 12.188 – 18.75)(10³) = 8.44 kJ
EXAMPLE
P
Find the internal energy for each state if P1 = 1000 kPa, V1 = 0.01 m³,
V2 = 0.025 m³, V3 = V4 = 0.04 m³, T1 = 400 K, T2 = 600K, n = 2 mol
1, (P1,V1) T1 Isobar
2, (P2,V2) T2
1. P2 = P1 = 1000 kPa
2. T4 = T1 = 400 K
3. T3 = T2 = 600 K
4. P3 = P2V2/V3 = 625 kPa
5. P4 = P1V1/V4 = 250 kPa
3, (P3,V3) T3
Isochore
4, (P4,V4) T4
6. U1 =  nRT1 = 9972 J
7. U4 = U1 = 9972 J
8. U2 =  nRT2 = 14958 J
9. U3 = U2 = 14958 J
V
EXAMPLE
Find the thermal energy change Q for each state if P1 = 1000 kPa,
V1 = 0.01 m³, V2 = 0.025 m³, V3 = V4 = 0.04 m³, T1 = 400 K, T2 = 600K,
n = 2 mol
Q12
P
1, (P1,V1) T1 Isobar
2, (P2,V2) T2
1. P2 = P1 = 1000 kPa
2. T4 = T1 = 400 K
3. T3 = T2 = 600 K
4. P3 = P2V2/V3 = 625 kPa
5. P4 = P1V1/V4 = 250 kPa
Q34
Q41
Q34
3, (P3,V3) T3
Isochore
4, (P4,V4) T4
10. Q12 = DU12 + W12 = 34986 J
11. Q23 = W23 (DU23 = 0) W23 =  (P2+P3)DV23 = 12.188 kJ
12. Q34 = DU34 = -4986 J
13. Q41 = W41 (U41 = 0) W41 =  (P4+P1)DV41 = - 18.75 kJ
V
6. U1 =  nRT1 = 9972 J
7. U4 = U1 = 9972 J
8. U2 =  nRT2 = 14958 J
9. U3 = U2 = 14958 J
Heat Engines and Refrigerators
The Wankel Rotary engine is a powerful and simple
alternative to the piston engine used by Nissan and
invented by the German, Wankel in the 1920s
The Wankel Cycle:
2 adiabats
2 isochores
The Wankel Engine