Download Summer-students-2009-part1 - Indico

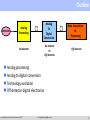
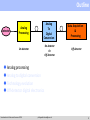
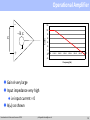
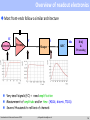
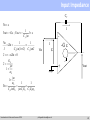
Introduction to Electronics in HEP Experiments
Philippe Farthouat
CERN
Introduction to Electronics Summer 2009
[email protected]
Credits and sources of information
 I have “stolen” a lot from the previous summer student lectures
from Christophe de la Taille and Jorgen Christiansen and from
colleagues from the PH electronics group (PH-ESE)
 Useful and more complete information can be found in the following
sites:
 CERN technical training ELEC 2005:
http://indico.cern.ch/conferenceDisplay.py?confId=62928
 LEB/LECC/TWEPP workshops from last 12 years:
http://lhc-electronics-workshop.web.cern.ch/lhc%2Delectronics%2Dworkshop/
 PH-ESE seminars:
http://indico.cern.ch/categoryDisplay.py?categId=1591
Introduction to Electronics Summer 2009
[email protected]
2
Outline
Detector
Analog
Processing
Analog
To
Digital
Conversion
On-detector
On-detector
Or
Off-detector
Data Acquisition
&
Processing
Off-detector
 Analog processing
 Analog to digital conversion
 Technology evolution
 Off-detector digital electronics
Introduction to Electronics Summer 2009
[email protected]
3
Outline
Detector
Analog
Processing
Analog
To
Digital
Conversion
On-detector
On-detector
Or
Off-detector
Data Acquisition
&
Processing
Off-detector
 Analog processing
 Analog to digital conversion
 Technology evolution
 Off-detector digital electronics
Introduction to Electronics Summer 2009
[email protected]
4
Analog Processing
 A few basic reminders
 Modelisation of the detector
 Charge and current amplifiers
 Noise
 Example of a preamplifier design
Introduction to Electronics Summer 2009
[email protected]
5
The foundations of electronics
 Voltage generators or source
 Ideal source : constant voltage,
independent of current (or load)
 In reality : non-zero source impedance RS
 Current generators
 Ideal source : constant current,
independent of voltage (or load)
 In reality : finite output source
impedance RS
 Ohms’ law
 Z = R, 1/jωC, jωL
 Note the sign convention
Introduction to Electronics Summer 2009
[email protected]
V RS → 0
RS → ∞
i
i
V
Z
6
Frequency domain & time domain
 Frequency domain :

V(ω,t) = A sin (ωt + φ)
 Described by amplitude and phase (A, φ)
Transfer function : H(ω) [or H(s)]
 The ratio of output signal to input signal in the
frequency domain assuming linear electronics
 Vout(ω) = H(ω) Vin(ω)

vin(ω)
H(ω)
vout(ω)
h(t)
vout(t)
F -1
 Time domain




Impulse response : h(t)
The output signal for an impulse (delta)
input in the time domain
The output signal for any input signal
vin(t) is obtained by convolution * :
Vout(t) = vin(t) * h(t) = ∫ vin(u) * h(t-u) du
vin(t)
 Correspondance through Fourier transforms
X()  Fx(t) 


 jt
x(t)
e
dt

 A few useful Fourier transforms in appendix below
Introduction to Electronics Summer 2009
[email protected]
7
Appendix: Fourrier Transform
F() 


 jt
x(t)
e
dt

Usualfunctions
 (t) 1
1
 (t) 
j
1
eat 
j  a
1
1 eat 
j ( j  a)
1
t n1eat 
( j  a) n
IMPEDANCES
Capacitor
Q  CV
I(t)  CV '(t)
I( )  CjV ( )
V ( )
1
Z( ) 

I( ) jC
Linearity
ah1 (t)  bh2 (t)  aF1 ( )  bF2 ( )
Inductor
V (t)  LI'(t)
V ( )  LjI( )
V ( )
Z( ) 
 jL
I( )
Integration,derivation
h(t)  F( ); h'(t)  jF( )
F( )
h(t)  F( );  h(t)dt 
j
Introduction to Electronics Summer 2009
[email protected]
8
Using Ohm’s law
 Example of photodiode readout
Used in high speed optical links
 Signal : ~ 10 µA when illuminated
 Modelisation :

volts
 Ideal current source Iin
 pure capacitance Cd
 Simple I to V converter : R

light
R = 100 kΩ gives 1V output for 10 µA
10 Gb/s optical receiver
 Speed ?
Transfer function H(ω) = vout/iin
 H has the dimension of Ω and is often called
« transimpedance » and even more often

(improperly) « gain »
H( ) 

1
jCd 
1
R

V
I in
Cd
100K
1
C d ( j 
1
)
RC d
1/RCd is called a « pole » in the transfer function
Introduction to Electronics Summer 2009
[email protected]
9
Frequency response
 Bode plot


Magnitude (dB) 20log H( )  20log
1
1
Cd ( j 
)
RC d
-3dB bandwidth : f-3dB = 1/2πRCd
Magnitude
100 dBΩ
80 dBΩ
 R=105Ω, Cd=10pF => f-3dB=160 kHz

 At f-3dB the signal is attenuated by 3dB = √2,
the phase is -45°

Above f-3dB , gain rolls-off at -20dB/decade
(or -6dB/octave)
Phase
Introduction to Electronics Summer 2009
[email protected]
10

Time response
 Impulse response
h(t)  F 1 (


R

1
1
Cd ( j 
)
RC d
)
10Gb/s eye
diagramresponse
(10 ps/div)
Impulse
t
exp( )

τ (tau) = RCd = 1 µs : time constant

 Step response : rising exponential
h(t)  F 1 (
1
1

)
j C ( j  1 )
d
RC d
pulse response
t
 R(1 exp( ))

 Rise time : t10-90% = 2.2 τ
 « eye diagram »
tr 10-90%
 Speed : ~ 10 µs = 100 kb/s !
 5 orders ofmagnitude away from a 10
Gb/s link !
Introduction to Electronics Summer 2009
[email protected]
11
Feedback
 Y is a source linked to X
 y=μx
 Open loop
 x=δe
 y=µx
 s=σy=σμδe
 Closed loop
x  e   y
y  x  e   y
e
y
1  
e
s  y 
1  
s


e 1  
Introduction to Electronics Summer 2009
e
x
µ
y
σ
δ
s
ß
 μ is the open loop gain
 βμ is the loop gain
[email protected]
12
Interest of feedback
e
x
µ
y
σ
δ
s
ß
 In electronics
 μ is an amplifier gain
 β is the feedback loop
 If μ is large enough the gain of the system is independent of the
amplifier gain
s




e 1   
Introduction to Electronics Summer 2009
[email protected]
13
Operational Amplifier
-
120
-A e
80
A (dB)
e
100
60
40
20
0
+
1.0E+00
-20
1.0E+01
1.0E+02
1.0E+03
1.0E+04
1.0E+05
1.0E+06
1.0E+07
-40
Frequency (Hz)
 Gain A very large
 Input impedance very high
 i.e input current = 0
 A(ω) as shown
Introduction to Electronics Summer 2009
[email protected]
14
How does it work?
 Direct gain calculation
Vin   e  I R1
Vout   Ae ; Vout  ( R1  R 2) I
Vout
A

Vin 1  A R1
R1  R 2
R2
-
-A e
e
 Feedback equation
s


e 1  
R1
;   1
R1  R 2
Vout
A

Vin 1  A R1
R1  R 2
I
R1
+
Vout
  A;  
Vin
 Ideal Opamp
A  ;
Vout R1  R 2

Vin
R1
Introduction to Electronics Summer 2009
[email protected]
15
Overview of readout electronics
 Most front-ends follow a similar architecture
fC
Detector
V
Preamp
V
Shaper
bits
ADC
DAQ
&
Processing
 Very small signals (fC) -> need amplification
 Measurement of amplitude and/or time (ADCs, discris, TDCs)
 Several thousands to millions of channels
Introduction to Electronics Summer 2009
[email protected]
16
Readout electronics : requirements
Low noise
High speed
Low power
Large
dynamic
range
High
reliability
Radiation
hardness
Low
cost !
Low
material
(and even less)
Introduction to Electronics Summer 2009
[email protected]
17
Detector(s)
 A large variety
 A similar modelization
PMT for Antares
6x6 pixels,4x4 mm2
CMS Pixel module
ATLAS Liquid Argon
Electromagnetic calorimeter
Introduction to Electronics Summer 2009
[email protected]
18
Detector modelization
 Detector = capacitance Cd
 Silicon : 0.1-10 pF
 PMs : 3-30pF
 Ionization chambers 10-1000 pF
 Signal : current source
 Silicon : ~1fC/100µm
 PMs : 1 photoelectron -> 105-107 e Wire chambers : a few 103 e Modelized as an impulse (Dirac) : i(t)=Q0δ(t)
I in
Cd
Detector modelisation
Typical PM signal
 Missing :
 High Voltage bias
 Connections, grounding
 Neighbours
 Calibration…
Introduction to Electronics Summer 2009
[email protected]
19
Reading the signal
 Signal
 Signal = current source
 Detector = capacitance Cd
 Quantity to measure
+
I in
Cd
 Charge => integrator needed + ADC
Time => discriminator + TDC
 Integrating on Cd
 Simple : V = Q/Cd
 « Gain » : 1/Cd : 1 pF -> 1 mV/fC
 Need a follower to buffer the voltage…
 Input follower capacitance : Ca // Cd
 Gain loss, possible non-linearities
 Crosstalk
 Need to empty Cd…
Introduction to Electronics Summer 2009
[email protected]
Q/Cd
Impulse response
20
Ideal charge preamplifier
 Ideal opamp in transimpedance
 Shunt-shunt feedback
 Transimpedance : vout/iin
Cf
-
 Vin-=0 =>Vout(ω)/iin(ω) = - Zf = - 1/jω Cf

Integrator : vout(t) = -1/Cf ∫ iin(t)dt
+
I in
Cd
vout(t) = - Q/Cf
« Gain » : 1/Cf : 0.1 pF -> 10 mV/fC
 Cf determined by maximum signal

 Integration on Cf
 Simple : V = - Q/Cf
 Unsensitive to preamp capacitance CPA
 Turns a short signal into a long one
 The front-end of 90% of particle physics
detectors…
 But always built with custom circuits…
Introduction to Electronics Summer 2009
[email protected]
Charge sensitive preamp
- Q/Cf
Impulse response
with ideal preamp
21
Non-ideal charge preamplifier
 Finite opamp gain

Z f
Vout ( )

Iin ( ) 1 Cd
G 0C f
Small signal loss in Cd / G0 Cf << 1
(ballistic deficit)

 Finite opamp bandwidth
 First order open-loop gain
 G(ω) = G0/(1 + j ω/ω0)
G0 : low frequency gain
G0ω0 : ωc gain bandwidth product
 Preamp risetime
 Due to gain variation with ω
 Time constant : τ (tau) = Cd / G0ω0 Cf
 Rise-time : t 10-90% = 2.2 τ
 Rise-time optimised with G0ω0 (ωc) or Cf
Introduction to Electronics Summer 2009
[email protected]
Impulse response with
non-ideal preamp
22
Input Impedance
Cf
Vin  e
I
1
Ie
Vout  Ge ; Vout  
C f j
1
1
Vin

 Zin 
C f j (1 G) C f jG
I
G    Zin  0
G0
G
j
1
I
Vin
e
+
0
1
Zin 
-G e
Vout
j
1
1
0


C f jG0 jC f G0 C f G0 0
Introduction to Electronics Summer 2009
[email protected]
23
Charge preamp seen from the input
 Input impedance with ideal opamp





Zin = Zf / G+1
Zin->0 for ideal opmap
« Virtual ground » : Vin = 0
Minimizes sensitivity to detector impedance
Minimizes crostalk
Input impedance of charge preamp
 Input impedance with real opamp
Z in 


1
1

jG0C f G0 0C f
Resistive term : Rin 
1
G0 0C f

1
 cC f
 Example : ωC = 109 rad/s Cf= 2 pF
=> Rin = 500Ω

Determines the input time constant :
t = ReqCd
 Good stability

Introduction to Electronics Summer 2009
[email protected]
24
Pile up
Rf
 It is necessary to discharge the
feedback capacitor
 Successive input pulses would
add up until saturation
 Several ways to do it, the simpler
being to put a resistor in parallel
Cf
-
-A e
+
Time
0
2
4
6
1.5
8
10
12
1
Input current
0.5
0
RC network
-0.5
-1
1
Input & Output
Input and Output
1.5
Capacitor only
Input current
0.5
0
-0.5
0
4
6
8
10
12
14
16
-1
Output
-1.5
-2
Time
-1.5
Introduction to Electronics Summer 2009
2
[email protected]
25
Crosstalk
 Capacitive coupling between
neighbours
 Crosstalk signal is differentiated
and with same polarity
 Small contribution at signal peak
 Proportionnal to Cx/Cd and
preamp input impedance
 Slowed derivative if RinCd ~ tp =>
non-zero at peak
 Inductive coupling
 Inductive common ground return
 “Ground apertures” = inductance
 Connectors : mutual inductance
Introduction to Electronics Summer 2009
[email protected]
26
Current preamplifiers
 Transimpedance configuration
 Vout()/iin() = - Rf / (1+Zf/GZd)
 Gain = Rf
 High counting rate
 Typically optical link receivers
Rf
Current sensitive
preamp
 Easily oscillatory
 Unstable with capacitive detector
 Inductive input impedance
1
 Resonance at : Fres 
2 Leq Cd
R
 Quality factor : Q 
L
eq
Cd
 Q > 
1/2 -> ringing

Damping with capacitance Cf in parallel

to Rf
 Easier with fast amplifiers
Step response of current sensitive preamp
Introduction to Electronics Summer 2009
[email protected]
27
Charge vs Current preamps
 Charge preamps
 Best noise performance
 Best with short signals
 Best with small capacitance
 Current preamps
 Best for long signals
 Best for high counting rate
 Significant parallel noise
Current
Charge
 Charge preamps are not slow, they are
long
 Current preamps are not faster, they are
shorter (but easily unstable)
Introduction to Electronics Summer 2009
[email protected]
28
Electronics noise
 Definition of Noise
 Random fluctuation superimposed to interesting signal
 Statistical treatment
 Three types of noise
 Fundamental noise (Thermal noise, shot noise)
 Excess noise (1/f …)
 Parasitics -> EMC/EMI (pickup noise, ground loops…)
Introduction to Electronics Summer 2009
[email protected]
29
Electronics noise
 Modelization
Noise generators : en, in
 Noise spectral density of en & in : Sv(f) & Si(f)

 Sv(f)
 Si(f)
Noise spectral density
= | F (en)|2 (V2/Hz)
= | F (in) |2 (A2/Hz)
 Rms noise Vn

Vn2 = ∫ en2(t) dt = ∫ Sv(f) df
 When going through a device H(2πf)

Svout(f) = |H(2πf)|2 Svin(f)
rms
Rms noise vn
Introduction to Electronics Summer 2009
[email protected]
30
Calculating electronics noise
 Fundamental noise
Thermal noise (resistors) : Sv(f) = 4kTR
 Shot noise (junctions) : Si(f) = 2qI
 1/f noise in CMOS devices

 Noise referred to the input
All noise generators can be referred to the input
as 2 noise generators :
 A voltage one en in series : series noise
 A current one in in parallel : parallel noise
 Two generators : no more, no less… why ?
Thermal noise generator

 To take into account the source impedance
en
Noiseless
 Golden rule
 Always calculate the signal before the noise
what counts is the signal to noise ratio
 Don’t forget noise generators are V2/Hz =>
calculations in module square
 Practical exercice next slide
Introduction to Electronics Summer 2009
Noisy
[email protected]
Noise generators referred to the input
31
Noise in charge pre-amplifiers
 2 noise generators at the input


Parallel noise : ( in2) (leakage
currents)
Series noise : (en2) (preamp)
 Output noise spectral density :
2
e
in  n 2
2
2
2
in
en C d
| Zd |
Sv ( ) 
 2 2
2
 2C f 2
 Cf
Cf
2


Noise spectral density
at Preamp output
Parallel noise in 1/ω2
Series noise is flat, with a
« noise gain » of Cd/Cf
 rms noise Vn
Parallel
noise
Vn2 = ∫ Sv(ω) dω/2π -> ∞ (!)
 Benefit of shaping…

Introduction to Electronics Summer 2009
[email protected]
Series
noise
32
Equivalent Noise Charge (ENC) after CRRCn
 Noise reduction by optimising useful
bandwidth
Step response of CR RCn shapers
Low-pass filters (RCn) to cut-off high frequency
noise
 High-pass filter (CR) to cut-off parallel noise
 -> pass-band filter CRRCn

 Equivalent Noise Charge : ENC






Noise referred to the input in electrons
ENC = Ia(n) enCt/√τ  Ib(n) in* √τ
Series noise in 1/√τ
Paralle noise in √τ
1/f noise independant of τ
Optimum shaping time τopt= τc/√2n-1
ENC vs tau for CR RCn shapers
 Peaking time tp (5-100%)

ENC(tp) independent of n
 Complex shapers are obsolete :
Power of digital filtering
 Analog filter = CRRC ou CRRC2

Introduction to Electronics Summer 2009
[email protected]
33
Equivalent Noise Charge (ENC) after CRRCn
 A useful formula : ENC (e- rms) after a CRRC2 shaper :
ENC  174
en Ctot
166in t p
tp
en in nV/ √Hz, in in pA/ √Hz are the preamp noise spectral densities
 Ctot (in pF) is dominated by the detector (Cd) + input preamp capacitance (CPA)
 tp (in ns) is the shaper peaking time (5-100%)


 Noise minimization
Minimize source capacitance
 Operate at optimum shaping
time
 Preamp series noise (en) best
with high trans-conductance
(gm) in input transistor

=> large current, optimal
size

Introduction to Electronics Summer 2009
[email protected]
34
ENC for various technologies
 ENC for Cd=1, 10 and 100 pF at ID = 500 uA
 MOS transistors best between 20 ns – 2 µs
 Parameters

Bipolar :







Introduction to Electronics Summer 2009
[email protected]
gm = 20 mA/V
RBB’=25 Ω
en= 1 nV/√Hz
IB=5uA
in = 1 pA/√Hz
CPA=100fF
PMOS 2000/0.35
 gm = 10 mA/V
 en = 1.4 nV/√Hz
 CPA = 5 pF

1/f :
35
MOS input transistor sizing
 Capacitive matching : strong inversion
 gm proportionnal to W/L √ID
 CGS proportionnal to W*L
 ENC propotionnal to (Cdet+CGS)/ √gm
 Optimum W/L : CGS = 1/3 Cdet
 Large transistors are easily in
moderate or weak inversion at small
current
© P O’Connor BNL
 Optimum size in weak inversion
 gm proportionnal to ID (indep of W,L)
 ENC minimal for CGS minimal, provided
the transistor remains in weak
inversion
Introduction to Electronics Summer 2009
[email protected]
36
Design in micro-electronics
 Performant design is at transistor level
 Simples models
 Hybrid π model
 Similar for bipolar and MOS
 Essential for desgin
 Three basic bricks
 Common emitter (CE) = V to I
(transconductance)
 Common collector (CC) = V to V
(voltage buffer)
 Common base (BC) = I to I
(current conveyor)
 Numerous « composites »
 Darlington, Paraphase, Cascode, Mirrors…
Introduction to Electronics Summer 2009
[email protected]
Low frequency hybrid model of bipolar
BC
CE
CC
37
Example : designing a charge preamp (1)
 From the schematic of principle
 Using of a fast opamp (OP620)
 Removing unnecessary components…
 Similar to the traditionnal schematic
«Radeka 68 »
 Optimising transistors and currents
Schematic of a OP620 opamp ©BurrBrown
Introduction to Electronics Summer 2009
[email protected]
Cf
+
Charge preamp ©Radeka 68
38
Example : designing a charge preamp (2)
 Simplified schematic
 Optimising components
 What transistors (PMOS, NPN ?)
 What bias current ?
 What transistor size ?
 What is the noise contributions
of each component, how to
minimize it ?
 What parameters determine the
stability ?
 Waht is the saturation
behaviour ?
 How vary signal and noise with
input capacitance ?
 How to maximise the output
voltage swing ?
 What the sensitivity to power
supplies, temperature…
Introduction to Electronics Summer 2009
Q1 : CE
IC1=500µA
Q2 : CB
IC2=100µA
Q3 : CC
IC3=100µA
Simplified schematic of charge preamp
[email protected]
39
Example : designing a charge preamp (3)
 Small signal equivalent model
 Transistors are reaplaced by hybrid π model
 Allows to calculate open loop gain
Small signal equivalent model of charge preamp
vin
gm1
vout
R0 C0
R0 = Rout2//Rin3//r04
 Gain (open loop) :
vout/vin = - gm1 R0 /(1 + jω R0 C0)
 Ex : gm1=20mA/V , R0=500kΩ, C0=1pF => G0=104 ω0=2106 G0ω0=2 1010 = 3 GHz !
Introduction to Electronics Summer 2009
[email protected]
40
Example : designing a charge preamp (4)
 Complete schematic

Adding bias elements
Input
Cf
Introduction to Electronics Summer 2009
[email protected]
Output
41
Example : designing a charge preamp (5)
 Complete simulation
 Checking hand calculations against 2nd order effects
 Testing extreme process parameters (« corner simulations »)
 Testing robustness (to power supplies, temperature…)
Saturation behaviour
Simulated open loop gain
10 ns 20 ns
Qinj=4.25 pC
Qinj=1.75 pC
Qinj=3.75 pC
Qinj=3.25 pC
Qinj=2.75 pC
Qinj=1.25 pC
Qinj=0.75 pC
Qinj=0.25 pC
mV
Qinj=2.25 pC
3.30
3.10
2.90
2.70
2.50
(V)
2.30
2.10
1.90
1.70
1.50
1.30
0.0
10
20
30
40
50
Time (ns)
1 MHz
Introduction to Electronics Summer 2009
[email protected]
42
Example : designing a charge preamp (6)
 Layout
 Each component is drawn
 They are interconnected by metal layers
 Checks
 DRC : checking drawing rules
(isolation, minimal dimensions…)



ERC : extracting the corresponding
electrical schematic
LVS (layout vs schematic) : comparing
extracted schematic and original design
Simulating extracted schematic with
parasitic elements
100 µm
 Generating GDS2 file
 Fabrication masks : « reticule »
Introduction to Electronics Summer 2009
[email protected]
43
Device available
 Acces to microelectronics
preamp
driver
Q1
FET
Cf
Q2
6 cm
Charge preamp in SMC hybrid techno
Q3
100 µm
Z0
Charge preamp in 0.8µm BiCMOS
Cf
Zf
Introduction to Electronics Summer 2009
[email protected]
44
Summary
 Charge sensitive preamplifiers
 Output proportionnal to the incoming charge
vout(t) = - Q/Cf
 « Gain » : 1/Cf : Cf = 1 pF -> 1 mV/fC
 Transforms a short pulse into a long one
 Low input impedance -> current sensitive
 Virtual resistance Rin-> stable with capacitive
detector
 The front-end of 90% of particle physics
detectors…
 But always built with custom circuits…
Charge preamplifier
architecture
 Noise minimization
 Minimize source capacitance
 Operate at optimum shaping time
 Preamp series noise (en) better with high
trans-conductance (gm) in input transistor
Introduction to Electronics Summer 2009
[email protected]
45