Download Angles

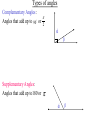
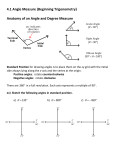
4.1 Radian and Degree
Measure
Trigonometry- from the Greek “measurement
of triangles”
Deals with relationships among sides and
angles of triangles and is used in astronomy,
navigation, and surveying.
Angles
• An angle is two rays with the same initial point.
• The measure of an angle is the amount of rotation
required to rotate one side, called the initial side, to
the other side, called the terminal side.
• The shared initial point of the two rays is called the
vertex of the angle.
Angles in standard position
• Standard position - the vertex is at the origin
of the rectangular coordinate system and the
initial side lies along the positive x-axis.
• If the rotation of the angle is in the
counterclockwise direction, then the angle is
said to be positive. If the rotation is
clockwise, then the angle is negative.
Coterminal Angles
• Two
angles in standard position that have the
same terminal side are said to be coterminal.
You find coterminal angles by adding or subtracting
2
Radians vs. Degrees
One radian is the central angle required to stretch the
radius around the outside of the circle.
Since the circumference of a circle is C  2r, it takes 2
radians to get completely around the circle once.
Therefore, it takes radians to get halfway around

the circle.
2
0, 2

3
2
Common Radian Angles, pg. 285
Angles between 0 and π/2 are acute
Angles between π/2 and π are obtuse
θ = π/2
Quad II
π/2 < θ < π
Quad I
0 < θ < π/2
θ=π
Quad III
Quad IV
π < θ < 3π/2
3π/2 < θ < 2π
θ = 3π/2
θ = 0,
2π
Types of angles
Complementary Angles :


Angles that add up to 90 or 2
ά
β
Supplementary Angles:
Angles that add up to 180or

ά
β
One degree is equivalent to a rotation of 1/360 of a
complete revolution about the vertex.
1 


180
radians
1radian 
180


To convert degrees to radians, multiply the degrees by

180
To convert radians to degrees multiply the radians by 180



Convert the following degree measures to
radian measure.
a) 120°
b)
−315°
c)
12°
Convert the following radian measures
to degrees.
a) 5π/6
b) 7


c)
7
Arc Length: For a circle of radius r, a central angle
θ intercepts an arc of length s given by s=rθ,
where θ is measured in radians
Example: Find the length of
the arc that subtends a
central angle with measure
120° in a circle with radius
5 inches
Angular and Linear Velocity
Angular Velocity (ω) is the speed at which



something rotates. Therefore,
which
t
means the rotation per unit time (how fast
something is going around a circle).
Linear Velocity (v) is the speed at which the outside
tip of the radius is traveling. Therefore, v = rω.
This equation considers the number of radii (since 
is expressed in radians) that travel around the
circle during the rotation process.
Example 1: A lawn roller with a 10-inch radius makes
1.2 revolutions per second.
a.) Find the angular speed of the roller in radians per
second.
b.) Find the speed of the tractor that is pulling the roller
in mi/hr.
Example 2: The second hand of a clock is 10.2 cm long.
Find the linear speed of the tip of this hand.
Example 3: An automobile is traveling at 65 mph. If
each tire has a radius of 15 inches, at what rate are the
tires spinning in revolutions per minute (rpm)?
Assignment:
• Page 291 # 5-21 odd, 35-65 odd, 75-85 odd,
95, 97