Download 4-1_Apply_Triangle_Sum_Properties

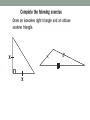
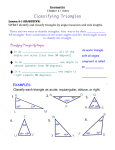
Warm up
right
OBJECTIVE:
Students will classify triangles by there
sides and angles and find missing angle
measurements in triangles
acute
obtuse
When lines are parallel
as indicated, the alt.
int. ’s 
OBJECTIVE:
Students will analyze and classify Triangles by sides &
angles, prove triangles congruent & use coordinate
geometry to investigate triangle relationships.
Why? Triangles are used to add strength to structures in
real-world situations. For example, the frame of a hang
glider involves several triangles.
Mastery is 80% or better on Practice Problems and 5Minute Checks.
Copy those terms for which you are unfamiliar
Skill Development
(3 ways)
0
2
3
Think….Ink…Share….Quick Write
• In your own words compare and contrast isosceles,
scalene and equilateral triangles.
• Hint: How are they similar? Different?
Skill Development
(4 ways)
equiangular
’s are also
equilateral
3
1
1
3
isosceles
72,72,36
acute isosceles
Pair Share
• With a partner discuss the criterion in the following
•
•
•
•
triangles:
Acute
Right
Obtuse
Equiangular
x
x
Skill Development
8
-1
-4
3
2
6
(-3-3)
(-3-5)
(3-5)
-
3
2
2
3
(3--1)
(3-2)
(-1-2)
RST is
a right 
right
-1
Two of the most important theorems you ever need
Guided
What
should we
do now?
3x – 9 = x + 73
2x = 82
x = 41
Guided ……White Boards
2x + x + 90 = 180
3x = 90
x = 30
 sum theorem
What kind of triangle is this?
Right scalene
Homework Day 1 of 2
• Page 221
• #1-15 all
Recall:
( sum corollary)
8x
x
How’s this for a challenge?
Hint: draw and label a picture
3x
x
2x
Which angle
is biggest?
A B C
Let x = the smallest angle
x + 2x + 3x = 180
6x = 180
x = 30
sum theorem
mA = 2(30) = 60
mB = 30
mC = 3(30) = 90
Don’t be afraid to recognize
properties we used last week
Notice the parallel lines
alt int ’s 
Y = 30
corollary to  sum
x = 60
OR
x + 30 = 90
x = 60
ext  theorem
Find y first
y = 90 – 39 = 51
corollary to  sum
Find this 
? = 180 – (50+51) = 79
x + 56 + 79 = 180
x = 45
 sum Theorem
Exit Slips
1.How many ways can a triangle be classified by its
sides? Name them.
2.How many ways can a triangle by classified by its
angles? Name them.
3.What do all the angles of any triangle ALWAYS add
up to? Name the theorem.
4.Find x and y. (copy picture)
WHAT WAS TODAYS OBJECTIVE
??
STUDENTS WILL ANALYZE
TRIANGLES, FIND THEIR
MEASURES AND CLASSIFY THEM
BY THEIR SIDES AND THEIR
ANGLES.
Home Work
• Pages 221-222
• #16-37 all