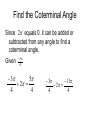Download 4.1 Radian and Degree measure

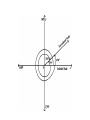
4.1 Radian and Degree
measure
Changing Degrees to Radians
Linear speed
Angular speed
Definition of an angle
An angle is made from two rays with a common initial point.
Ter min al
side
Initial
side
In standard position the initial side is on the x axis
Positive angle vs. Negative angle
Positive angles are Counter clockwise
C.C.W.
Negative angles are Clockwise
C.W.
Angles with the same initial side and
terminal side are coterminal.


The measure of an angle is from
initial side to terminal side
Vertex at the origin (Center)
r
Central
Angle

r
Definition of a Radian
Radian is the measure of the arc of a unit
circle.
Unit circle is a circle with a radius of 1.
The quadrants in terms of Radians
What is the circumference of a circle with
radius 1?
The quadrants in terms of Radians
What is the circumference of a circle with
radius 1?
2
1
0 2
The quadrants in terms of Radians
The circumference can be cut into parts.

2

1
3
2
0 2
The quadrants in terms of Radians
The circumference can be cut into parts.
I
II

2

2
 

  
III
3
2
1
3
2
0  
0 2
3
   2
2
IV

2
Find the Coterminal Angle
Since 2 equals 0. it can be added or
subtracted from any angle to find a
coterminal angle.
Given  3
4
 3
5
 2 
4
4
 3
 11
 2 
4
4
Radian vs. Degree measurements
360º = 2
180º = 
So

1 

180
rad
or
Radian vs. Degree measurements
360º = 2
180º = 
So

1 

180
rad
or
1 rad 
180

To convert Degrees into Radians multiply by 
180
To convert Radians into Degrees multiply by
180

Change 140º to Radians
7
Change 3 to degrees
Use

180
degree to rads.

140
7
140 *

    2.443460953
180 180
9
Use
180

rads to degrees
7 180 1260
*

 420
3

3
How to use radian to find Arc length
The geometry way was to find the
circumference of the circle and multiply by
the fraction. Central angle
360º
In degrees Are length called S would be
S

360
2r 
How to use radian to find Arc length
In degrees Are length called S would be
S

360
2r 
In radian the equation is
S  r
r = 9, θ = 215º
Changing to rads


43
215 

180 36
r
Are length S
43
S
9
36
43
S
 33.772
4
Linear speed and Angular speed
Linear speed is arc  length  S
time
t
Angular speed is Central angle  
time
Assuming “constant speed”
t
Homework
Page 269 – 272
# 9, 12, 17, 23,
25, 31, 37, 40,
47, 57, 62, 67,
71, 75, 79, 83,
87, 91, 99, 102
Homework
Page 269 – 272
# 11, 15, 19, 24,
27, 35, 39, 43,
55, 59, 65, 70,
73, 77, 81, 85,
89, 93, 100, 108