* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 3.1 What Are Congruent Figures?
Survey
Document related concepts
Dessin d'enfant wikipedia , lookup
Technical drawing wikipedia , lookup
Golden ratio wikipedia , lookup
Multilateration wikipedia , lookup
Euler angles wikipedia , lookup
Tessellation wikipedia , lookup
Apollonian network wikipedia , lookup
Line (geometry) wikipedia , lookup
History of geometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Transcript
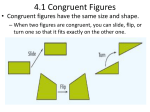
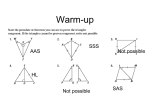
Congruent figures 3.1 What Are Congruent Figures? Cade Levinson Pricci Honors Geometry 9 Part 1: Congruent • What is Congruent • Congruent figures have all sides and angles the same size and shape. • Therefore congruent can be defined as any figure with the same size and shape. • For example… Look! Flying Pie! Get it Pie! Pi! Math puns!!! These two triangles have the exact same size and shapes. Congruent triangles need to have all 6 parts (angles + sides) to be equal. This is true with the 2 above triangles. So triangle ABC is congruent to triangle DEF. But… Does that mean that triangle ABC is also congruent to triangle FED? NOOOOOO! The thing is… • When naming congruent figures, the points have to match up. Since point A is not equal to point F, triangle ABC would not equal Triangle FED. Polygons reflect! (Pikachu counters!) • Definition: Congruent polygons have all pairs of corresponding parts congruent. • Reflections of polygons are congruent since all of their parts are the same size and shape. • Each reflection also shares a similar part down the middle. Such as… These Ducks This leads to the Reflexive Property which states : Any segment or angle is congruent to itself. Sample Problem A E B D F C Given: E and F bisect segments AB and DC respectively. ABCD is a rectangle Are Parallelograms AEFD and EBCF congruent Since E and F bisect the segments those sides are congruent. In a triangle, the opposite sides and angles are congruent . Yes the two figures are congruent. Practice Problem • A B Triangle BFE C E F If E is the midpoint of segment CF, Triangle ACE is congruent to which other triangle? Works Cited • Rhoad, Richard, Milauskas George, and Whipple Robert. Geometry for Enjoyment and Challenge. Evanston: McDougal, Littell & Company, 1997. • Feliz, Mike. "Geometry 3.2 Congruent Triangles". Free Math Help. May 15 2008 <http://www.freemathhelp.com/felizcongruent-triangles.html>.