Download right triangles - Cloudfront.net

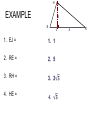
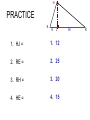
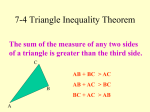
CHAPTER 8:
RIGHT TRIANGLES
8.1
SIMILARITY IN RIGHT
TRIANGLES
RIGHT TRIANGLE
• Recall that triangles can be named by
angle measures and side lengths.
• A right triangle is identified by angle
measure and has the following
characteristics:
– 1 right angle (90° angle)
– 2 acute angles (angles less than 90°)
– A hypotenuse and 2 legs
RIGHT TRIANGLE
A right triangle is shown below with all sides
and angles named:
Acute
angle
hypotenuse
leg
Right
angle
Acute
angle
leg
RADICALS
The solutions to problems involving radicals
should always be written in simplest radical
form:
1. No perfect square factor other than 1 is under the
radical sign.
2. No fraction is under the radical sign.
3. No fraction has a radical in its denominator.
EXAMPLES
PROPORTIONS
GEOMETRIC MEAN
EXAMPLE
YOU TRY
Find the geometric mean:
1. Between 5 and 10
2. Between 6 and 8
3. Between 9 and 15
4. Between 2 and 72
SIMILARITY IN POLYGONS
Remember that if two polygons are similar,
then the following holds true:
1. Corresponding angles are congruent;
2. Corresponding sides are in proportion.
We use the symbol ~ to represent similarity.
THEOREM 8-1
THEOREM 8-1
If the altitude is drawn to the hypotenuse of a
right triangle, then the two triangles formed
are similar to the original triangle and to each
other.
C
A
R
B
∆ACB ~ ∆ARC ~ ∆CRB
COROLLARY 1
C
A
R
B
COROLLARY 2
C
A
R
B
H
EXAMPLE
2
E
1. EJ =
2. RE =
3. RH =
4. HE =
J
4
R
H
PRACTICE
E
9
J
1. HJ =
1. 12
2. RE =
2. 25
3. RH =
3. 20
4. HE =
4. 15
16
R
CLASSWORK/HOMEWORK
8.1 Assignment
• Pgs. 287-288, Classroom Exercises 2-16
even
• Pgs. 288-289, Written Exercises 2-38
even