Download Big Trouble in Little Geometry

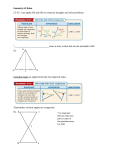
Big Trouble in Little Geometry
Chapter 5.1: The Indirect Proof
By Steve Sorokanich
The Indirect Proof?!
• The indirect proof, also
• known as Modus Tollens,
• or “Proof by Contradiction”
in Latin, uses negation
of a fact in order to
prove another fact to
also be a negative.
Pshhh. Yeah Right!
Well, let’s put it this way, a regular proof
Goes through the logic “If p, then q” or
“p => q”. An example of this would be
Proving two triangles congruent by SSS.
It follows that “If three sides of one triangle are
Congruent to the three sides of another triangle,
Then the two triangles are congruent to
Each other.”
What’s So Great about
Indirect Proofs?
• Indirect proofs are the contrapositive of direct
proofs. They follow the logic of
“if not q, then not p” or “~q => ~p”. When q
and p rely on each other in order to be true,
then when q is negated, p is also negated. In
our example, if it is proven that three sides of
a triangle are not congruent, then it follows
that the triangles are not congruent to each
other because if they were congruent, all
three pairs of sides would be congruent.
The Golden Form of Indirect
Proofs
Indirect Proofs follow several steps in
Order to create an organized, logical proof.
1.
List the possiblilities for the conclusion
2.
Assume that the negation of the desired conclusion is correct.
3.
Write a chain of reasons until you reach an impossibility. This
will be a contradiction of either
(a) given information or
(b) a theorem, definition, or other known fact.
4.
State the remaining possibility as the desired conclusion
It’s as simple as 1, 2, 3a, 3b, 4!
Le Examples
Either ray RS bisects angle PRQ or RS does
not bisect Angle PRQ
Assume ray RS bisects angle PRQ
Then angle PRS is congruet to angle QRS
(bisector divides an angle into 2
congruent angles)
It is given that seg RS is perpendicular to PQ,
so that angle PSR an angle QSR are
right angles (perpendicular angles form
right angles) and angle PSR is congruent
to angle QSR (right angles are
congruent)
Since segments RS and RS are congruent
through reflexive property, then triangle
PSR is congruent to triangle QSR (ASA).
Therefore, segments PR and QR are
congruent (CPCTC).
But this is impossible because it contradicts
the given fact that segments PR and QR
are not congruent.
Therefore the assumption is false and it
follows that ray RS does not bisect angle
PRQ because that is the only other
possibility.
Chapter 5 Packet 1,
page 1, problem 1
Practice Problem
Either
Assume
It is given that
But it is impossible Because it
contradicts
Therefore the assumption is false and it
follows that
Because that is the only other possibility
Chapter 5, Packet 1,
Page 1 Problem 2
Practice Problem…Solution
Either angle AOB is congruent to angle BOC
or angle AOB is not congruent to BOC
Assume that angle AOB is congruent to angle
BOC
It is Given That Circle O, so segments AO and
OC are congruent (all radii of a circle are
congruent). Since segment BO is
congruent to BO (Reflexive), then triangle
BAO is congruent to triangle BCO (SAS).
Therefore segements AB and BC are
congruent by CPCTC.
But this is impossible because it contradicts
the given fact that segment AB is not
congruent to segment BC.
Therefore the assumption is false and it
follows that angle AOB is not congruent
to angle BOC because that is the only
other possibility
References
• Calkins,Keith J. “A Review of Basic Geometry,
Lesson 11: Direct and Indirect Proofs. 30
May,2008. Andrews University.
<http://www.andrews.edu/~calkins/m
ath/webtexts/geom11.htm>.
Geometry for Enjoyment and Challenge. Chapter
5, section 1, The Indirect Proof.