Download Rectangular Prisms

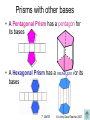
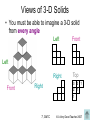
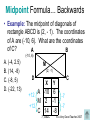
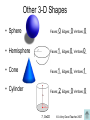
Exit Level
TAKS Preparation Unit
Objective 7
© A Very Good Teacher 2007
Nets and 3-D figures
• When given a net, try to imagine what it
would look like when folded up.
• Here are some common nets:
7, Gb1B
© A Very Good Teacher 2007
Cubes and Rectangular Prisms
• The net of a cube is made entirely of
squares
• The net of a rectangular prism contains
rectangles
7, Gb1B
© A Very Good Teacher 2007
Pyramids
• The net of a triangular pyramid has a
triangle for its base
• The net of a square pyramid has a
square for its base
7, Gb1B
© A Very Good Teacher 2007
Prisms with other bases
• A Pentagonal Prism has a pentagon for
its bases
• A Hexagonal Prism has a hexagon for its
bases
7, Gb1B
© A Very Good Teacher 2007
Use your imagination!
• Example: The net below can be folded to
form a cube. Which cube could be formed
from this net?
A.
B.
C.
D.
7, Gb1B
© A Very Good Teacher 2007
Views of 3-D Solids
• You must be able to imagine a 3-D solid
from every angle
Left
Front
Right
Top
Left
Front
Right
7, Gd1C
3 2 1
2 1
1
© A Very Good Teacher 2007
Views of 3-D Solids, cont…
• Example: The 3-dimensional figure shown
below represents a structure that Jessica
built with 11 cubes. Which of the following
best represents the top view of Jessica’s
structure?
Front
A.
B.
C.
D.
Right
7, Gd1C
© A Very Good Teacher 2007
Quadrilaterals (four sided figures)
• Rectangle
• Square
• Rhombus
Isosceles
Trapezoid
• Trapezoid
• Parallelogram
7, Gd2A
© A Very Good Teacher 2007
Other Important Shapes
• Pentagon – five sided
• Hexagon – six sided
• Regular – perfect shape
– All sides congruent
– All angles congruent
7, Gd2A
© A Very Good Teacher 2007
The Coordinate Plane
y-axis
An ordered
pair (point) is
graphed by
Quadrant II
using the x to
move right or
left and the y
to move up or
down
Quadrant III
(x, y)
(2, 5)
Quadrant I
(-3, -5)
x-axis
Quadrant IV
7, Gd2A
© A Very Good Teacher 2007
Key Geometry Terms
• Collinear – points that lie in the same line
• Non Collinear – points that do not lie in
the same line
7, Gd2A
© A Very Good Teacher 2007
Classifying Triangles
• By Sides
– Equilateral: equal sides
– Isosceles: 2 sides the same
– Scalene: no sides the same
• By Angles
– Equiangular: equal angles
– Acute: all angles less than 90˚
– Obtuse: one angle greater than 90˚
– Right: one angle equal to 90˚
© A Very Good Teacher 2007
Parallel and Perpendicular Lines
6
5
4
3
2
1
• Parallel Lines
– have the same slope (m)
Rise
m
Run
-6 -5 -4 -3 -2 -1
• Perpendicular Lines
1

2
-6 -5 -4 -3 -2 -1
2

1
7, Gd2B
1 2 3 4 5 6
-1
-2
-3
-4
-5
-6
6
5
4
3
2
1
– have opposite
reciprocal slopes
y
-1
-2
-3
-4
-5
-6
1

2
1

2
x
1

2
y
x
1 2 3 4 5 6
2

1
© A Very Good Teacher 2007
Interpreting Parallel and
Perpendicular Situations
• Example: Which of the following best
describes the graph of the equations below?
y = -3x + 6
m = -3
y = 6 – 3x
1
1
3y = x + 6
m
y  x2
3
3
3
3 3
A. The lines have the same x-intercept
B. The lines have the same y-intercept
Perpendicular
Lines!
C. The lines intersect to form right angles
D. The lines are parallel to each other
7, Gd2B
© A Very Good Teacher 2007
Distance Formula
• To find the distance between 2 points on a
graph use the DISTANCE FORMULA
d  ( x2  x1 )  ( y2  y1 )
2
2
• Example: What is the approximate length
of XY when the xcoordinates
ofy its
y
x
1
2 2
1
endpoints are (-3, -9) and (5, 2)?
A. 13.6
B. 7.3
C. 9.1
D. 11.7
d
5  3   2  9
d
8  11
2
2
d  64  121
7, Gd2C
2
2
d  185
© A Very Good Teacher 2007
Distance by Graphing
• Example: What is the approximate length of XY
when the coordinates of its endpoints are (-3, -9)
and (5, 2)?
A.
B.
C.
D.
8 units
13.6
7.3
9.1
11.7
11 units
7, Gd2C
© A Very Good Teacher 2007
Midpoint Formula
• To find the midpoint between two points on
the graph use the MIDPOINT FORMULA!
 x1  x2 y1  y2 
,


2 
 2
• Example: Find the midpoint of the line
segment whose endpoints are (5.75, 2) and
(-3.25, 9).  5.75   3.25 2  9   2.5 11 
,

=  2 ,2
2
2  


= 1.25,5.5
7, Gd2C
© A Very Good Teacher 2007
Midpoint Formula… Backwards
• Example: The midpoint of diagonals of
rectangle ABCD is (2, - 1). The coordinates
of A are (-10, 6). What are the coordinates
of C?
A
B
(-10, 6)
A. (-4, 2.5)
B. (14, -8)
C. (-8, 5)
D. (-22, 13)
M
(2, -1)
D
X
-10
+12 A
C
Y
6
M 2 -1
+12
C 14 -8
7, Gd2C
-7
-7
© A Very Good Teacher 2007
Faces, Edges and Vertices
• Faces are sides
• Edges are lines
• Vertices are corners
5
8 Vertices: __
5
Faces: __,
__,
7 Edges: 15
10
7, Ge2D
© A Very Good Teacher 2007
Other 3-D Shapes
• Sphere
0 Edges:__,
0 Vertices:__
0
Faces:__,
• Hemisphere
Faces:__,
1 Edges:__,
0 Vertices:__
0
• Cone
1 Edges:__,
0 Vertices:__
1
Faces:__,
• Cylinder
Faces:__,
2 Edges:__,
0 Vertices:__
0
7, Ge2D
© A Very Good Teacher 2007