Download Geometry

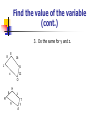
Geometry
Lesson 4.3A
Similarity
T.2.G.1 Apply congruence (SSS …) and similarity (AA …) correspondences and properties
of figures to find missing parts of geometric figures and provide logical justification
M.3.G.4 Use (given similar geometric objects) proportional reasoning to solve practical
problems (including scale drawings)
M.3.G.5 Use properties of parallel lines and proportional reasoning to find the lengths of
segments
CGT.5.G.5 Draw and interpret the results of transformations and successive
transformations on figures in the coordinate plane
translations
reflections
rotations (90˚, 180˚, clockwise and counterclockwise about the origin)
dilations (scale factor)
Two polygons are similar if:
1. Corresponding angles are congruent
2. Corresponding sides are
proportional
Similarity Ratio

Similarity Ratio – the ratio of the lengths of
corresponding sides of similar triangles
A
15
B
D
10
12
C
18
E
8
12
F
Similarity Ratio
Corresponding angles are congruent. (Mark
congruent angles)

A
15
B
D
10
12
C
18
E
8
12
F
Similarity Ratio

To write the similarity statement, keep the
corresponding vertices in the same order:
ABC ~ DEF
A
15
B
D
10
12
C
18
E
8
12
F
Similiarity Ratio

To write the similarity ratio, write the ratio of
the corresponding sides and simplify.
A
15
10
12
C
B
E
8
F
12
18

AB 15 3


DE 10 2
D
AC 12 3


DF
8 2
BC 18 3


EF 12 2
The similarity ratio is 3
2
Find the value of the variable.
Given: LOVE  MATH

8
E
1. Find the similarity ratio.
16
L
V
x
LE 8 4
 
MH 6 3
12
O
6
H
z
T
M
y
9
A
Find the value of the variable
(cont.)
8
E
16
L
V
x
12
O
H
6
z
M
9
A
T
y
2. Write a proportion and
solve for x.
Find the value of the variable
(cont.)
3. Do the same for y and z.
E
8
16
L
V
x
12
O
H
6
z
M
9
A
T
y
Use the given information to solve
for x (round to the nearest tenth.)

Given ABC; DE || BC .
A
1. Since
15
7
D
DE || BC,
E
then B
 D and
C  E.
3
B
x
C
2. Therefore,
ABC ~ ADE
Use the given information to solve
for x (round to the nearest tenth.)
Continued
Since ABC ~ ADE , we can write a
proportion to solve for x.

A
15
7
D
E
3
B
x
C
Use the given information to solve
for x (round to the nearest tenth.)

Given ABC;
A
x
D
6
E
4
B
9
C
DE
||
BC
.
Use the given information to solve
for x (round to the nearest tenth.)

a
b
c
Given a || b || c.
10
17
x
30
•If parallel lines are cut by a
traversal, the segments between the
parallel lines are proportional.
•We can set up a proportion to
solve for x.