Download Document

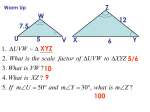
Similar triangles are triangles that have the same
shape but not necessarily the same size.
A
D
E
B
F
C
ABC  DEF
When we say that triangles are similar there are several
repercussions that come from it.
A  D
B  E
C  F
AB
DE
=
BC
EF
=
AC
DF
Six of those statements are true as a result of the
similarity of the two triangles. However, if we need to
prove that a pair of triangles are similar how many of
those statements do we need? Because we are working
with triangles and the measure of the angles and sides
are dependent on each other. We do not need all six.
There are three special combinations that we can use
to prove similarity of triangles.
1. PPP Similarity Theorem
 3 pairs of proportional sides
2. PAP Similarity Theorem
 2 pairs of proportional sides and congruent
angles between them
3. AA Similarity Theorem
 2 pairs of congruent angles
E
1. PPP Similarity Theorem
 3 pairs of proportional sides
A
9.6
5
B
C
12
mAB

mDF
mBC

mFE
5
 1.25
4
12
 1.25
9.6
F
4
mAC
13

 1.25
mDE 10.4
ABC  DFE
D
2. PAP Similarity Theorem
 2 pairs of proportional sides and congruent
angles between them
L
G
70
H
7
I
mGH
5

 0.66
7.5
mLK
mHI
7

 0.66
mKJ 10.5
70
J
10.5
mH = mK
GHI  LKJ
K
The PAP Similarity Theorem does not work unless
the congruent angles fall between the proportional
sides. For example, if we have the situation that is
shown in the diagram below, we cannot state that the
triangles are similar. We do not have the information
that we need.
L
G
50
H
7
I
J
50
K
10.5
Angles I and J do not fall in between sides GH and HI and
sides LK and KJ respectively.
3. AA Similarity Theorem
 2 pairs of congruent angles
Q
M
70
50
N
mN = mR
mO = mP
O
50
70
P
MNO  QRP
R
It is possible for two triangles to be similar when
they have 2 pairs of angles given but only one of
those given pairs are congruent.
T
X
Y
34
34
59
59
Z
87 59
U
S
mS = 180- (34 + 87)
mS = 180- 121
mS = 59
mT = mX
mS = mZ
TSU  XZY
Yes
Yes
No
Yes
Yes
Yes
Practice 2:
A
D
E
C
B
• Triangle ABC is similar to triangle
ADE.
• DE is parallel to BC.
• AE = 3 cm, EC = 6 cm, DE = 4cm
• Calculate the length of BC
Answer :
A
3
4
D
E
9
6
B
A
12
C
AC = 9 = 3
AE 3
BC = 3
DE
BC = 3 x DE
BC = 3 x 4 = 12
…and then…
AB & DE are parallel
Explain why ABC is similar to CDE
5
A
B
<CED = <BAC Alternate Angles
<EDC = <ABC Alternate Angles
<ECD = <ACB Vert Opp Angles
3
C
6
E
D
?
Triangle ABC is similar to Triangle CDE
…and then…
Calculate the length of DE
AC corresponds to CE
Scale Factor = 2
5
A
B
AB corresponds to DE
DE = 2 x AB
3
C
DE = 10cm
6
E
D
?