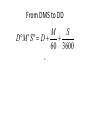Download Section 4.1 - Shelton State Community College

Section 4.1
Angles and Radian Measure
The Vocabulary of Angles
• An angle is formed by two rays that have a
common endpoint.
• One ray is called the initial side and the other
is called the terminal side.
• The common endpoint is called a vertex.
• Angles are often named with lowercase Greek
letters.
Some familiar vocabulary
• Angles are measured in degrees.
• A complete rotation measures 360 degrees.
• An acute angle measures more than 0 but less
than 90 degrees.
• An obtuse angle measures more than 90, but
less than 180 degrees.
• A right angle measures 90 degrees.
• A straight angle measures 180 degrees.
Radians
• Angles are also measured in radians.
• To define a radian, we must first define a central
angle (a central angle is an angle who vertex is
the center of a circle)…
• …and an intercepted arc (an intercepted arc is the
portion of the circle between the two rays of a
central angle).
• One radian is the measure of a central angle
whose intercepted arc is the same length as the
radius of the circle.
The relationship between radians and
degrees
360  2
radians
Other equivalences follow from
dividing the circle into
“reasonable” portions.
Conversions
• To convert from degrees to radians multiply by

180
• To convert from radians to degrees multiply by
180

More vocabulary
• An angle is in standard position if
1. Its vertex is at the origin
2. Its initial side lies along the positive x-axis
• Counterclockwise rotation from the initial
side to the terminal side means the angle is
positive.
• Clockwise rotation from the initial side to the
terminal side means the angle is negative.
Still more vocabulary
• When the terminal side of an angle lies in a
quadrant, we say that the angle lies in that
quadrant.
• When the terminal side of an angle lies on the
x-axis or y-axis, we say that the angle is
quadrantal.
Draw the following and give the
quadrant or axis
270 
 60
5
6

radians
radians
Coterminal Angles
• Two angles with the same initial and terminal
sides but possibly different rotations are called
coterminal angles.
• Adding or subtracting a multiple of 360
degrees or 2”pi” radians will result in a
coterminal angle.
Examples
• Find a coterminal angle between 0 and 360
degrees or 0 and 2”pi” radians for each of the
570
following:
 70
17
5

11
3
Arc Length
• Consider a circle of radius r with a central
angle of measure “theta” (in radians). The
measure s of the intercepted arc is given by
s  r
Examples
1.
2.
3.
4.
Find s if r = 4 cm and “theta” = 2 radians
Find r if s = 10 in and “theta” = 3 radians
Find “theta” if s = 7.5 m and r = 5 m
Find s if r = 8 ft and “theta” = 120 degrees
Converting from DMS to Decimal
Degrees (and vice versa)
• “DMS” stands for Degrees-Minutes-Seconds.
• The conversions are based on subdivisions of a
whole degree:
• 1 degree = 60 minutes
• 1 minute = 60 seconds
• It follows that 1 degree = 3600 seconds
From DMS to DD
M
S
D M ' S "  D 

60 3600
29
From DD to DMS
1. Multiply the decimal part of the degrees (to
the right of the decimal point) by 60. These
are your minutes.
2. Now multiply the decimal part of your
minutes (to the right of the decimal point) by
60. These are your seconds.
Examples
• 35 degrees 23 minutes 57 seconds to DD
(round to four decimal places)
• 97.55 degrees to DMS