Download Document

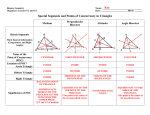
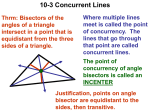
POINTS OF CONCURRENCY
In this lesson we will define what a point of concurrency is.
Then we will look at 4 points of concurrency in triangles.
As you go through the powerpoint, you will complete your
notesheet.
You will need to be able to define the 4 points of
concurrency and identify them in a picture. You will also
use the definition to identify relationships between
Segments and angles to solve problems.
POINTS OF CONCURRENCY
When two lines intersect at one point, we say that the lines
are intersecting. The point at which they intersect is
the point of intersection.
(nothing new right?)
Well, if three or more lines intersect, we say that the lines
are concurrent. The point at which these lines intersect
Is called the point of concurrency.
Perpendicular bisectors=Circumcenter
The perpendicular bisectors of the sides of a triangle are
concurrent at a point equidistant from the vertices.
Point of concurrency
Perpendicular bisectors=Circumcenter
This point of concurrency has a special name. It is known
as the circumcenter of a triangle.
Circumcenter
Perpendicular bisectors=Circumcenter
The circumcenter is equidistant from all three vertices.
Perpendicular bisectors=Circumcenter
The circumcenter gets its name because it is the center of
the circle that circumscribes the triangle. Circumscribe
means to be drawn around by touching as many points as
possible.
Perpendicular bisectors=Circumcenter
Sometimes the circumcenter will be inside the triangle,
sometimes it will be on the triangle, and
sometimes it will be outside of the triangle!
Acute
Right
Obtuse
Angle bisectors=Incenter
The bisectors of the angles of a triangle are
concurrent at a point equidistant from the sides.
Angle bisector
Angle bisectors=Incenter
The point of concurrency of the three angle bisectors is
another center of a triangle known as the Incenter. It is
equidistant from the sides of the triangle, and gets its
name from the fact that it is the center of the circle that is
inscribed within the circle.
Incenter
Medians=Centroid
Median: A median of a triangle is the segment That
connects a vertex to the midpoint of the opposite side.
Medians=Centroid
This point of concurrency of the medians is another
center of a triangle. It is known as the Centroid.
Centroid
Medians=Centroid
This Centroid is also the Center of Gravity of a triangle
which means it is the point where a triangular shape will
balance.
Altitudes=Orthocenter
Altitudes of a triangle are the perpendicular
segments from the vertices to the line containing
the opposite side.
Unlike medians, and angle bisectors that are
always inside a triangle, altitudes can be inside,
on or outside the triangle.
Altitudes=Orthocenter
This point of concurrency of the altitudes of a triangle
form another center of triangles. This center is known
as the Orthocenter.
The Orthocenter of a triangle can be inside
on or outside of the triangle.
POINTS OF CONCURRENCY
There are many Points of Concurrency in Triangle. We
have only looked at four:
Circumcenter: Where the perpendicular bisectors meet
Incenter: Where the angle bisectors meet
Centroid: Where the medians meet
Orthocenter: Where the altitudes meet.
Practice Problems
On the half sheet of paper that you were given
complete the following problems.
1A-C Identify the point of concurrency that is shown
in the triangle
A
B
C
Practice Problems
Solve for x, y in each triangle using the given information
2. Point G is a centroid
AC = 24, AF=15,
AE= 3x-6, BF = 3y
3. Point H is an orthocenter
<ABE = 25, <BFC = 8x + 10,
<BAE= 6y+5
Practice Problems
4. Point W is both a centroid and an orthocenter.
Why is it a circumcenter also?
5. If you draw two medians, is that enough to determine
where the centroid of a triangle is? Why/Why not?
6. Do the following matching.
A. Circumcenter
B. Incenter
C. Orthocenter
D. Centroid
W. Angle bisectors
X. Medians
Y. Perpendicular bisectors
Z. Altitudes