* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Vertical Angles, Linear Pair, and Bisector
Survey
Document related concepts
Transcript
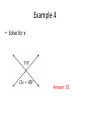
Answers to Homework Page 40 5)Yes, they share a common side and vertex with no common interior points. 7)No they are supp 8)No they are comp 9)m<AOB or m<COD 10)<EOC 11) <EOC 12)<DOC 14)yes, they are marked 16)No they are not marked. 17)Yes, they form a line 18)Yes they are marked 19)No they are not marked 20)Yes they form a line 39)C 40)I 41)See Board 42)<WXY 43)<WXZ, <YXZ 44)39 Vertical Angles and Linear Pair September 8, 2011 • Objective: You will be able to identify and solve problems with vertical angles and linear pairs. • Bell Ringer: Solve for x 2x + 53 x+7 Angle Pairs • Vertical Angles: Two angles whose sides are opposite rays. The angles are congruent. (They form an X) • Linear Pair: Two angles that share a common ray and form a line. (The angles are supplementary) Example • <KPL and <JPL form a linear pair. If m<KPL = 2x + 24 and m<JPL = 4x + 36, what are the measures of the two angles? 2x + 24 + 4x + 36 = 180 Linear Pairs are Supplementary Combine Like Terms 6x + 60 = 180 6x = 120 Subtract 60 x = 20 Divide by 6 m<KPL = 2(20) + 24 = 64 Substitute 20 for x m<JPL = 4(20) + 36 = 116 Example • Solve for x and then find the measure of the two angles. 6x + 18 = 8x – 2 6x + 20 = 8x 20 = 2x 10 = x 6(10) + 18 = 78 Vertical Angles are Congruent Add 2 to both sides Subtract 6x from both sides Divide by 2 Substitute 10 for x Bisector • An angle bisector is a ray that divides two angles into two congruent angles. • Example: Ray CF bisects <ACE, find the value of x and the measure of <ACE. 5x = 2x + 24 3x = 24 x=8 5(8) + 2(8) + 24 = 80 Definition of a bisector Subtract 2x from both sides Divide both sides by 3 Substitute 8 for x Example 1 • Find the value of x. Answer: 23 Example 2 • Find the value of x. Answer: 20 Example 3 • Find the value of x. Answer: 8 Example 4 • Solve for x Answer: 35 Example 5 • Ray BT bisects <ABC, find the value of x Answer: 10 Example 6 • Solve for x Answer: 31 Example 7 • Ray BT bisects angle ABC. Solve for x. Answer: 5